
- •Сверху вниз: упругое тело, левая отсеченная часть, правая отсеченная часть Рис.1. Метод сечений.
- •Эпюры внутренних усилий при растяжении-сжатии
- •Эпюры внутренних усилий при кручении
- •Дифференциальные зависимости между внутренними усилиями при изгибе
- •Напряженное состояние в точке. Тензор напряжений
- •Тензор деформации
- •Потенциальная энергия упругой деформации
- •Механические состояния деформируемых тел
- •Диаграммы упруго-пластического деформирования конструкционных материалов
- •Постановка задач теории надежности
- •Расчетные нагрузки, коэффициенты запаса
- •Расчеты по допускаемым нагрузкам и по допускаемым напряжениям
- •Напряжения при растяжении (сжатии) призматических стержней. Расчет на прочность
- •Понятие о концентрации напряжений, принцип сен-венана
- •Определение деформаций и перемещений
- •Напряженное состояние при растяжении (сжатии)
- •Применение к статически определимым системам.
- •Расчет статически неопределимых систем по способу допускаемых нагрузок.
- •Подбор сечений с учетом собственного веса (при растяжении и сжатии).
- •Деформации при действии собственного веса.
- •Вычисление моментов инерции и моментов сопротивления для простейших сечений.
- •Общий способ вычисления моментов инерции сложных сечений.
- •Наибольшее и наименьшее значения центральных моментов инерции.
- •Рациональные формы поперечных сечений при изгибе
- •Понятие о составных балках
- •Б) а) несвязанная конструкция, б) связанная сварная конструкция Рис.1. Расчетные схемы составных балок:
- •Дифференциальное уравнение прямого изгиба призматического стержня
- •Расчет валов
- •Понятие о сдвиге. Расчет заклепок на перерезывание.
- •А) расчетная схема, б) действующие усилия Рис.2. Соединение с накладками:
- •90 120 С двумя накладками.
- •А) расчетная схема б) линейное и нелинейное сопротивления Рис.1. Модели изгиба балки:
- •Изгиб балки при действии продольных и поперечных сил.
- •Внецентренное сжатие или растяжение.
- •Примем следующий порядок расчета.
- •3. Строится эпюра крутящего момента Мz.
- •Подбор сечений балок равного сопротивления.
- •Определение деформаций балок переменного сечения.
- •Общие понятия.
- •Расчет бесконечно длинной балки на упругом основании, загруженной одной силой р.
- •Постановка задачи.
- •Вычисление потенциальной энергии.
- •Расчетная модель к теореме Кастильяно.
- •Примеры приложения теоремы Кастильяно.
- •Теорема Максвелла—Мора.
- •Метод Верещагина.
- •А) расчетная схема б)грузовая эпюра в)фиктивное состояние г) эпюра моментов от единичного момента Рис.4. Иллюстрация метода Верещагина:
- •Общие понятия и метод расчета.
- •Способ сравнения деформаций.
- •А) исходная модель, б) фиктивная модель нагружения, в) грузовая эпюра моментов, г) эпюра моментов от реакции в, д) единичная эпюра моментов Рис.2. Решение методом Мора и Верещагина
- •Выбор лишней неизвестной и основной системы.
- •Общий план решения статически неопределимой задачи.
- •Определение деформаций статически неопределимых балок.
- •Связи, накладываемые на систему. Степень статической неопределимости.
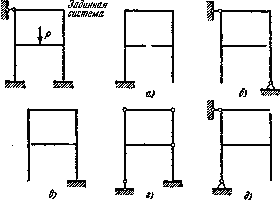
- •А) плоская, б) плоскопространственная. В) пространственная Рис.2. Расчетные схемы рамных конструкций:
- •А)внешняя связь, б) две внешние связи в) шесть внешних связей в общем случае Рис.3. Схемы эквивалентных связей
- •А) три внешних связи, б) пять внешних связей Рис.4. Плоская рама
- •А) кинематически неизменяемая, б) неопределимая внутренним образом, в)со снятием дополнительных связей Рис.5. Классификационные признаки рам:
- •А) статически неопределимая — семь, б) — три, в) — четыре, г) — три, е) — двенадцать, ж) — семь, д) — три, и) — тринадцать раз статически неопределима Рис.6. Примеры рамных конструкций:
- •А) , б) и Рис.5. Интерпретация коэффициентов уравнений метода сил:
- •Напряжения в сферических толстостенных сосудах.
- •Диск равного сопротивления.
- •Формула Эйлера для определения критической силы.
- •Влияние способа закрепления концов стержня.
- •Проверка сжатых стержней на устойчивость.
- •Основные характеристики цикла и предел усталости
- •А) растяжение, б) изгиб, в) контактные напряжения Рис.1. Очаги концентрации местных напряжений:
- •Влияние состояния поверхности и размеров детали на усталостную прочность
- •Коэффициент запаса усталостной прочности и его определение
- •Постановка задачи. Явление Резонанса.
- •Влияние резонанса на величину напряжений.
- •Вычисление напряжений при колебаниях.
- •Учет массы упругой системы при колебаниях.
- •Основные положения
- •Общий прием вычисления динамического коэффициента при ударе.
- •А) двухопорная балка, б) консольная Рис.2. Модели удара:
А) кинематически неизменяемая, б) неопределимая внутренним образом, в)со снятием дополнительных связей Рис.5. Классификационные признаки рам:
Рассмотрим теперь несколько примеров определения степени статической неопределимости стержневых и рамных систем. На рис. 6 показано несколько рам. Последовательно рассмотрим их.
а) Рама имеет четыре дополнительные внешние связи и три взаимные связи, т. е. семь раз статически неопределима.
б) Полагаем сначала, что шарнир А отсутствует. Тогда имеются две внешние и три внутренние дополнительные связи. Система без шарнира А была бы пять раз статически неопределимой.
Шарнир А принадлежит одновременно трем стержням. Его можно рассматривать как два совпавших шарнира (рис. 7). Так как каждый шарнир снимает одну связь, т. е. разрешает поворот одного сечения относительно другого, то можно сказать, что шарнир А снимает две связи. Система становится, таким образом, вместо пяти — три раза статически неопределимой.
Обобщая сказанное, можно сделать вывод, что шарнир снимает число связей, на единицу меньшее числа сходящихся в нем стержней. В данном случае в шарнире А сходятся три стержня и шарнир снимает две связи.
А) статически неопределимая — семь, б) — три, в) — четыре, г) — три, е) — двенадцать, ж) — семь, д) — три, и) — тринадцать раз статически неопределима Рис.6. Примеры рамных конструкций:
в) Если бы шарнир А отсутствовал, система была бы четыре раза внешним образом и три раза внутренним образом статически неопределимой, т. е. всего семь раз. Шарнир А снимает число связей, на единицу меньшее числа сходящихся в нем стержней, т. е. три связи. Рама четыре раза статически неопределима.
г) Рама три раза статически неопределима.
д) Внешние связи не удовлетворяют условиям кинематической неизменяемости. Это — механизм, точнее говоря, мгновенный механизм. Система имеет возможность поворачиваться относительно верхней опоры как жесткое целое Понятно, что угол поворота будет небольшим. Нижняя связь заклинится и будет достигнуто какое-то положение равновесия, но новое положение связей будет зависеть от жесткости системы. К раме неприменимы основные принципы сопротивления материалов: принцип неизменности начальных размеров и принцип независимости действия сил.
![]() Рис.7.
модель двух совпадших шарниров
Рис.7.
модель двух совпадших шарниров
е) Рама — пространственная. Имеется шесть дополнительных внешних связей (лишняя заделка) и шесть дополнительных взаимных связей (замкнутый контур) Система 12 раз статически неопределима.
ж) Система семь раз статически неопределима (один раз внешним образом и шесть раз — внутренним).
з) Здесь для плоской рамы не показаны внешние связи, но дана система внешних сил, удовлетворяющая условиям равновесия. В таком случае условились считать, что дополнительных внешних связей нет, и положение рамы в пространстве считается определенным; рассматриваются только внутренние связи. Система три раза статически неопределима.
и) Здесь также рассматриваются только внутренние связи, поскольку система указанных внешних сил удовлетворяет условиям равновесия. Нужно подсчитать, сколько сечений необходимо сделать в раме, чтобы, с одной стороны, она не «рассыпалась», а с другой, чтобы в ней не осталось ни одного замкнутого контура. Таких сечений следует сделать пять (см. рис. 6, и). Система 30 раз статически неопределима.
Лекция № 38. Метод сил.
Наиболее широко применяемым в машиностроении общим методом раскрытия статической неопределимости стержневых и рамных систем является метод сил. Он заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так и взаимных, а их действие заменяется силами и моментами. Величина их в дальнейшем подбирается так, чтобы перемещения в системе соответствовали тем ограничениям, которые накладываются на систему отброшенными связями. Таким образом, при указанном способе решения неизвестными оказываются силы. Отсюда и название «метод сил». Такой прием не является единственно возможным. В строительной механике широко применяются и другие методы, например метод деформаций, в котором за неизвестные принимаются не силовые факторы, а перемещения в элементах стержневой системы.
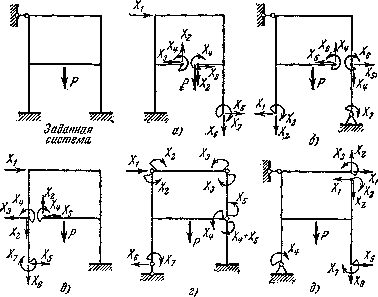
Итак, раскрытие статической неопределимости любой рамы методом сил начинается с отбрасывания дополнительных связей. Система, освобожденная от дополнительных связей, становится статически определимой. Она носит название основной системы.
 а-д)
модификации основной системы
Рис.1.
пример стержневой рамы:
а-д)
модификации основной системы
Рис.1.
пример стержневой рамы:
Для каждой статически неопределимой стержневой системы можно подобрать, как правило, сколько угодно основных систем. Например, для рамы, показанной на рис. 1, можно предложить основные системы, а), б),..., которые получены путем отбрасывания семи дополнительных связей в различных комбинациях. Вместе с тем нужно помнить, что не всякая система с семью отброшенными связями может быть принята как основная. На рис. 2 показано три примера для той же рамы, в которой также отброшено семь связей, однако сделано это неправильно, так как оставшиеся связи не обеспечивают кинематической неизменяемости системы, с одной стороны, и статической определимости во всех узлах,— с другой.
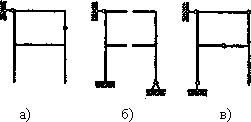 Рис.2.Некорректные
преобразования заданной системы в
основные по причине кинематической
изменяемости- а) б), или статической
определимости во всех узлах — в)
Рис.2.Некорректные
преобразования заданной системы в
основные по причине кинематической
изменяемости- а) б), или статической
определимости во всех узлах — в)
После того как дополнительные связи отброшены и система превращена в статически определимую, необходимо, как уже говорилось, ввести вместо связей неизвестные силовые факторы. В тех сечениях, где запрещены линейные перемещения, вводятся силы. Там, где запрещены угловые смещения, вводятся моменты. Как в том, так и в другом случае неизвестные силовые факторы будем обозначать Xi-, где i — номер неизвестного. Наибольшее значение i равно степени статической неопределимости системы. Заметим, что для внутренних связей силы Xi, — являются взаимными. Если в каком-либо сечении рама разрезана, то равные и противоположные друг другу силы и моменты прикладываются как к правой, так и к левой частям системы.
 а)-д)
по отношению к заданной системе
Рис.3.
Пять разновидностей основных систем
а)-д)
по отношению к заданной системе
Рис.3.
Пять разновидностей основных систем
Основная система, к которой приложены все внешние заданные силы и неизвестные силовые факторы, носит название эквивалентной системы. На рис. 3 показано пять эквивалентных систем, которые соответствуют приведенным выше основным системам (рис. 1). Принцип приложения неизвестных силовых факторов становится ясным без дальнейших пояснений.
Теперь остается составить уравнения для определения неизвестных.
Обратимся к некоторому конкретному примеру. Рассмотрим, например, первую эквивалентную систему из числа представленных на рис. 3,4. Тем, что рассматривается конкретно взятая семь раз статически неопределимая система, общность рассуждений не будет нарушена.
Перейдем
теперь к составлению уравнений для
определения неизвестных силовых
факторов. Условимся через
![]() обозначать
взаимное смещение точек системы.
обозначать
взаимное смещение точек системы.
 Рис.4.
Пример расчета рамы а)по выбранной
основной системе- б)
Рис.4.
Пример расчета рамы а)по выбранной
основной системе- б)
Первый
индекс при
![]() соответствует
направлению перемещения, а второй —
силе, вызвавшей это перемещение.
соответствует
направлению перемещения, а второй —
силе, вызвавшей это перемещение.
В рассматриваемой раме в точке А отброшена неподвижная опора. Следовательно, горизонтальное перемещение здесь равно нулю и можно записать:
![]()
Индекс 1 означает, что речь идет о перемещении по направлению силы Х1, а индекс [Х1, Х2,..., Р] показывает, что перемещение определяется суммой всех сил, как заданных, так и неизвестных.
Аналогично можно записать:
![]()
![]()
Так
как под величиной
![]() понимается
взаимное смещение точек, то
понимается
взаимное смещение точек, то
![]() обозначает
вертикальное смещение точки В
относительно С,
обозначает
вертикальное смещение точки В
относительно С,
![]() —
горизонтальное взаимное смещение тех
же точек,
—
горизонтальное взаимное смещение тех
же точек,
![]() есть
взаимное угловое смещение сечений В
и С.
Угловым смещением будет также в
рассматриваемой системе величина
есть
взаимное угловое смещение сечений В
и С.
Угловым смещением будет также в
рассматриваемой системе величина
![]() .
.
В
точках A
и D
смещения
![]() являются
абсолютными. Но абсолютные смещения
можно рассматривать как смещения,
взаимные с неподвижными отброшенными
опорами. Поэтому принятые обозначения
приемлемы для всех сечений системы.
являются
абсолютными. Но абсолютные смещения
можно рассматривать как смещения,
взаимные с неподвижными отброшенными
опорами. Поэтому принятые обозначения
приемлемы для всех сечений системы.
Пользуясь
принципом независимости действия сил,
раскроем выражения для перемещений
![]()
![]()
![]()
Аналогичным
образом запишем и остальные пять
уравнений: каждое из слагаемых
![]() ,
входящих в уравнение, обозначает
перемещение в направлении силы с первым
индексом под действием силы, стоящей
во втором индексе. Поскольку каждое
перемещение пропорционально соответствующей
силе, величину
,
входящих в уравнение, обозначает
перемещение в направлении силы с первым
индексом под действием силы, стоящей
во втором индексе. Поскольку каждое
перемещение пропорционально соответствующей
силе, величину![]() можно записать в следующем виде:
можно записать в следующем виде:
![]()
Что
касается перемещений
![]() ,
,
![]() и
т. д., то под индексом Р
будем понимать не просто внешнюю силу
Р,
а вообще систему внешних сил, которая
может быть произвольной Поэтому величины
и
т. д., то под индексом Р
будем понимать не просто внешнюю силу
Р,
а вообще систему внешних сил, которая
может быть произвольной Поэтому величины
![]() ,
,
![]() ,...
в уравнениях оставим неизменными.
,...
в уравнениях оставим неизменными.
Теперь уравнения примут вид:
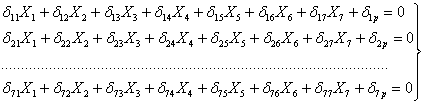
Эти
уравнения являются окончательными и
носят название канонических
уравнений метода сил.
Число их равно степени статической
неопределимости системы. В некоторых
случаях, как увидим далее, когда имеется
возможность сразу указать значения
некоторых неизвестных, число совместно
решаемых уравнений снижается. Остается
теперь выяснить, что представляют собой
коэффициенты
![]() и
как следует их определять. Для этого
обратимся к выражению (6.1).
и
как следует их определять. Для этого
обратимся к выражению (6.1).
Если
![]() ,
то
,
то
![]()
Следовательно,
коэффициент
![]() это
есть перемещение по направлению i-го
силового фактора под действием единичного
фактора, заменяющего k-й
фактор. Например, коэффициент
это
есть перемещение по направлению i-го
силового фактора под действием единичного
фактора, заменяющего k-й
фактор. Например, коэффициент
![]() уравнения
представляет собой взаимное горизонтальное
смещение точек B
и С,
которое возникло бы в раме, если бы к
ней вместо всех сил была приложена
только единичная сила в точке А
(рис. 5 а). Если, например, вместо сил
уравнения
представляет собой взаимное горизонтальное
смещение точек B
и С,
которое возникло бы в раме, если бы к
ней вместо всех сил была приложена
только единичная сила в точке А
(рис. 5 а). Если, например, вместо сил
![]() приложив
единичные силы, а все прочие силы с
эквивалентной системы снять (рис. 5 б),
то угол поворота в сечении D
под действием этих сил будет
приложив
единичные силы, а все прочие силы с
эквивалентной системы снять (рис. 5 б),
то угол поворота в сечении D
под действием этих сил будет
![]() ,
горизонтальное перемещение в точке А
будет
,
горизонтальное перемещение в точке А
будет
![]() и
т. д.
и
т. д.
