Примеры приложения теоремы Кастильяно.

   Определим (Рис.4) прогиб свободного конца В балки, защемленной другим концом А. Балка нагружена сосредоточенной силой, приложенной в точке В. В данном случае возможно непосредственное применение теоремы Кастильяно, так как отыскивается прогиб сечения, где приложена сосредоточенная сила Р

Рис.4. Пример расчетной схемы для расчета перемещений.

 

   Начало отсчета абсциссы х сечения можно выбирать произвольно, лишь бы формула для М (х) была возможно проще. Отсчитывая х от точки В, получаем для момента в любом сечении балки

и

Подставляя эти значения в формулу для и интегрируя, чтобы охватить всю длину балки от 0 до l, получаем:

Лекция № 34. Теоремы о взаимности работ и Максвелла — Мора.

   Пользуясь понятием о потенциальной энергии, можно установить следующую зависимость между деформациями в различных сечениях балки.

   Если к балке, нагруженной силой приложить затем статически силу в сечении 2, то к прогибу точки приложения силы от этой же силы прибавится (Рис.1) прогиб от силы , равный ; первый значок у буквы у указывает точку, для которой вычисляется прогиб; второй — обозначает силу, вызывающую этот прогиб.

Рис.1. Расчетная схема к теореме о взаимности работ

 

   Полная работа внешних сил составится из трех частей: работы силы на вызванном ею прогибе , т. е. , работы силы на вызванном ею прогибе ее точки приложения , т. е. , наконец, работы силы на прогибе ее точки приложения от силы , т. е. .

Таким образом, накопленная в стержне при действии обеих сил энергия будет равна:

   Это количество энергии деформации зависит лишь от конечных значений сил и прогибов и не зависит от порядка нагружения.

   Если к балке, загруженной силой , приложить затем силу то, повторив цепь вычислений, получим:

Сравнивая оба значения U, получаем:

т. е. работа силы (или первой группы сил) на перемещениях, вызванных силой (второй группой сил), равна работе силы на перемещениях, вызванных силой .

   Это и есть теорема о взаимности работ. Ее можно сформулировать и иначе: работа первой силы () при действии второй () равна работе второй силы при действии первой.

 

Теорема Максвелла—Мора.

Прогиб балки в точке приложения сосредоточенной силы Р равен:

аналогичное выражение мы имеем и для угла поворота с заменой производной на . Выясним, что представляют собой эти производные.

   Если на балке расположена какая угодно нагрузка из сосредоточенных сил , , ,..., моментов , ,..., сплошных нагрузок ,..... то момент М(х) в любом сечении такой балки выражается линейной функцией от нагрузок:

Рис.2. Частная расчетная модель метода Максвелла — Мора.

 

   Коэффициенты , ,..., , …, , ... являются функциями пролета балки, расстояний точек приложения сил и моментов от опор и абсциссы х взятого сечения. Пусть мы отыскиваем прогиб точки приложения силы ; тогда

так как , ,..., , ,..., ,..., , ,..., , …, , ... при этом дифференцировании постоянны. Но можно рассматривать как численную величину момента М в любом сечении балки от действия так называемой единичной нагрузки, т. е. силы ; действительно, подставляя в формулу вместо его частное значение, единицу, и приравнивая все остальные нагрузки нулю, получаем .

Например, для балки, изображенной на Рис2, а, изгибающий момент равен:

   Производная ; но это как раз и будет выражение изгибающего момента нашей балки, если мы ее нагрузим силой 1, приложенной в той же точке В, где расположена сила Р (Рис.2, б), и направленной в ту же сторону.

   Аналогично, производная изгибающего момента М (х) по паре сил численно представляет собой изгибающий момент от пары с моментом, равным единице, приложенной в том же сечении, где имеется пара , и направленной в ту же сторону. Таким образом, вычисление производных изгибающего момента можно заменить вычислением изгибающих моментов от единичной нагрузки. Эти моменты мы будем обозначать буквой .

   Таким образом, для отыскания перемещения (прогиба или угла поворота) любого сечения балки, вне зависимости от того, приложена или не приложена в этом сечении соответствующая сила, необходимо найти выражение для изгибающего момента М от заданной нагрузки и момента от соответствующей единичной нагрузки, приложенной в сечении, где ищем перемещение ; тогда это перемещение выразится формулой

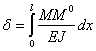
   Эта формула была предложена Максвеллом в 1864 г. и введена в практику расчета О. Мором в 1874 г. Если мы в полученном выражении под подразумеваем прогиб, то момент надо вычислять от сосредоточенной единичной силы, приложенной в той точке, где мы отыскиваем прогиб; при вычислении же угла поворота в качестве единичной нагрузки прикладывается пара сил с моментом, равным единице.

Для примера рис.2 имеем:

	(рис.2,а)
	(рис.2, б)

   Знак плюс означает, что направление перемещения совпадает с направлением единичной нагрузки, знак минус — наоборот.

   Если при определении изгибающих моментов придется делить балку на участки, то соответственно и интеграл в формуле распадется на сумму интегралов.

   Сравнивая формулу Кастильяно с формулой Мора, нетрудно заметить, что они отличаются лишь одним множителем. В теореме Кастильяно или , в теореме Мора .

   Следовательно, производная от изгибающего момента по обобщенной силе — это то же самое, что изгибающий момент от силы .