А) расчетная схема б) линейное и нелинейное сопротивления Рис.1. Модели изгиба балки:

 

   Известно, что косой изгиб имеет место, когда силы, его вызывающие, не лежат в одной из главных плоскостей инерции. Однако, если разложить внешние силы по главным осям инерции Ох и Оу, то получим две системы сил P_1x, P_2x, …, P_nx и P_1y, P_2y,..., P_ny, каждая из.которых вызывает прямой изгиб с изгибающими моментами соответственно M_y и М_x (рис. 2). Применяя принцип независимости действия сил, нормальные напряжения (рис. 3) определим как алгебраическую сумму напряжений от M_x и М_y:

   Чтобы не связывать себя формальными правилами знаков, слагаемые будем определять по модулю, а знаки ставить по смыслу. Прогибы балки определим как геометрическую сумму прогибов от прямых изгибов (рис. 2)

.

   Таким образом, расчет на косой изгиб с применением принципа независимости действия сил сводится к расчету на два прямых изгиба с последующим алгебраическим суммированием напряжений и геометрическим суммированием прогибов.

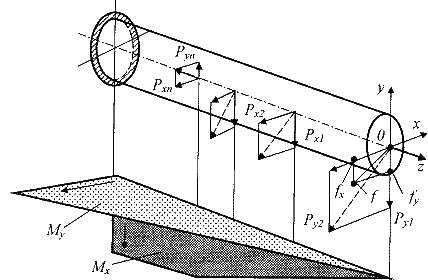Рис.2. Расчетная модель косого изгиба бруса

 

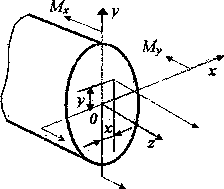Рис.3. Связь нормального напряжения с внутренними изгибающими моментами

 

   В случае поперечных сечений, имеющих две оси симметрии и выступающие угловые точки (рис. 4) с равными по модулю и максимальными одноименными координатами и напряжения в этих точках будут равны

   Слагаемые в этом выражении рекомендуется определять по модулю, а знаки ставить по смыслу. Например, на рис. 5 верхний ряд знаков «+» и «—» соответствует напряжениям от М_x, а нижний ряд — от M_y, и напряжения в этих точках будут равны

Рис.4. Симметричные варианты сечений

 

Рис.5. Расстановка знаков от действия моментов

 

Условие прочности для балок из пластичного материала с указанным типом сечений запишется в виде

 

   В остальных случаях для определения max а (или max dp и max для хрупкого материала) необходимо по общей формуле проверить напряжения во всех подозрительных точках.

   Есть и другой путь: положив , получим уравнение нейтральной линии. Так как напряжения в точках поперечного сечения будут пропорциональными расстояниям от нейтральной линии, то max будут возникать в наиболее удаленных от нее точках.

Лекция № 27. Совместное действие изгиба и растяжения или сжатия.

Изгиб балки при действии продольных и поперечных сил.

   На практике очень часто встречаются случаи совместной работы стержня на изгиб и на растяжение или сжатие. Подобного рода деформация может вызываться или совместным действием на балку продольных и поперечных сил, или только одними продольными силами.

   Первый случай изображен на Рис.1. На балку АВ действуют равномерно распределенная нагрузка q и продольные сжимающие силы Р.

Рис.1. Совместное действие изгиба и сжатия.

 

   Предположим, что прогибами балки по сравнению с размерами поперечного сечения можно пренебречь; тогда с достаточной для практики степенью точности можно считать, что и после деформации силы Р будут вызывать лишь осевое сжатие балки.

   Применяя способ сложения действия сил, мы можем найти нормальное напряжение в любой точке каждого поперечного сечения балки как алгебраическую сумму напряжений, вызванных силами Р и нагрузкой q.

   Сжимающие напряжения от сил Р равномерно распределены по площади F поперечного сечения и одинаковы для всех сечений:

нормальные напряжения от изгиба в вертикальной плоскости в сечении с абсциссой х, которая отсчитана, скажем, от левого конца балки, выражаются формулой

Таким образом, полное напряжение в точке с координатой z (считая от нейтральной оси) для этого сечения равно

   На Рис.2 изображены эпюры распределения напряжений в рассматриваемом сечении от сил Р, нагрузки q и суммарная эпюра.

   Наибольшее напряжение в этом сечении будет в верхних волокнах, где оба вида деформации вызывают сжатие; в нижних волокнах может быть или сжатие или растяжение в зависимости от числовых величин напряжений и . Для составления условия прочности найдем наибольшее нормальное напряжение.

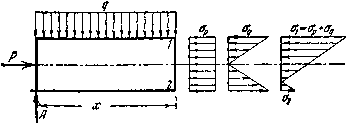Рис.2. Сложение напряжений сжатия и изгиба

 

   Так как напряжения от сил Р во всех сечениях одинаковы и равномерно распределены, то опасными будут волокна, наиболее напряженные от изгиба. Такими являются крайние волокна в сечении с наибольшим изгибающим моментом; для них

Таким образом, напряжения в крайних волокнах 1 и 2 среднего сечения балки выражаются формулой

,

и расчетное напряжение будет равно

Если бы силы Р были растягивающими, то знак первого слагаемого изменился бы, опасными были бы нижние волокна балки.

Обозначая буквой N сжимающую или растягивающую силу, можем написать общую формулу для проверки прочности:

(27.1)

Описанный ход расчета применяется и при действии на балку наклонных сил. Такую силу можно разложить на нормальную к оси, изгибающую балку, и продольную, сжимающую или растягивающую.