
- •Введение
- •Требования к аппаратным средствам
- •Установка аппаратной защиты
- •Копирование файлов системы на жесткий диск
- •Как пользоваться этим Руководством
- •Условности и сокращения
- •Новые возможности
- •Техническая поддержка и сопровождение
- •Глава 1. Интерфейс системы
- •1.1. Панель свойств
- •1.1.1. Управление состоянием Панели свойств
- •1.1.2. Работа с Панелью свойств
- •1.1.3. Настройка оформления Панели свойств
- •1.2. Компактные панели
- •1.3. Настройка интерфейса
- •1.3.1. Настройка состава Главного меню и панелей инструментов
- •1.3.2. Создание пользовательской Инструментальной панели
- •1.3.3. Настройка клавиш быстрого вызова команд («горячих клавиш»)
- •1.3.4. Утилиты
- •1.4. Вид приложения
- •1.5. Настройка цветов
- •1.5.1. Цвет фона
- •1.5.2. Цвет курсора
- •1.5.3. Цвет элементов
- •Глава 2. Среда черчения и моделирования
- •2.1. Типы документов
- •2.1.1. Трехмерные модели
- •2.1.2. Графические документы
- •2.1.3. Текстовые документы
- •2.2. Единицы измерения длины
- •2.3. Единицы измерения углов
- •2.4. Представление чисел
- •2.5. Системы координат
- •Глава 3. Запуск системы
- •Глава 4. Приемы работы с документами
- •4.1. Создание
- •4.2. Открытие
- •4.3. Сохранение
- •4.3.1. Сохранение документа под другим именем
- •4.3.2. Сохранение всех документов
- •4.4. Закрытие
- •4.5. Свойства документа
- •4.6. Шаблоны документов
- •Глава 5. Управление окнами документов
- •5.1. Закладки документов
- •5.2. Разделение рабочей области
- •Глава 6. Управление отображением документа в окне
- •6.1. Изменение масштаба изображения
- •6.1.1. Увеличение и уменьшение масштаба изображения
- •6.1.2. Явное задание масштаба изображения
- •6.1.3. Увеличение масштаба произвольного участка изображения
- •6.1.4. Масштаб по выделенным объектам
- •6.1.5. Плавное изменение масштаба
- •6.1.6. Отображение документа целиком
- •6.1.7. Переход к предыдущему или последующему масштабу отображения
- •6.1.8. Автоматический подбор масштаба
- •6.2. Сдвиг изображения
- •6.2.1. Линейки прокрутки
- •6.2.2. Листание документов
- •6.3. Управление порядком отрисовки объектов
- •6.4. Обновление изображения
- •Глава 7. Базовые приемы работы
- •7.1. Курсор и управление им
- •7.2. Использование контекстных меню
- •Глава 8. Приемы создания объектов
- •8.1. Параметры объектов
- •8.1.1. Указание точек в окне документа
- •8.1.2. Ввод параметров в предопределенном порядке
- •8.1.3. Ввод значений в поля Панели свойств
- •8.1.4. Фиксация параметров
- •8.1.5. Освобождение параметров
- •8.1.6. Активизация параметров
- •8.1.7. Запоминание параметров
- •8.1.8. Отображение параметров объектов рядом с курсором
- •8.1.9. Округление значений параметров
- •8.1.10. Автоматическое и ручное создание объектов
- •8.1.11. Повторное указание объектов
- •8.1.12. Перебор объектов
- •8.1.13. Прерывание команды
- •8.2. Привязка
- •8.2.1. Глобальная привязка
- •8.2.2. Локальная привязка
- •8.2.3. Клавиатурная привязка
- •8.2.4. Ортогональное черчение
- •8.3. Геометрический калькулятор
- •8.4. Отмена и повтор действий
- •8.5. Выделение объектов
- •8.5.1. Выделение объектов мышью
- •8.5.2. Выделение объектов с помощью команд
- •8.5.3. Расширенное выделение объектов
- •8.5.4. Настройка выделения
- •8.6. Использование сетки
- •8.6.1. Привязка по сетке
- •8.6.2. Настройка параметров сетки
- •8.6.3. Изображение сетки при мелких масштабах
- •8.7. Использование ЛСК
- •8.7.1. Создание локальной системы координат
- •8.7.2. Управление локальными системами координат
- •8.7.3. Настройка отображения систем координат
- •8.8. Использование буфера обмена
- •8.8.1. Помещение объектов в буфер
- •8.8.2. Вставка из буфера
- •Глава 9. Общие сведения о геометрических объектах
- •9.1. Стили геометрических объектов
- •9.1.1. Выделение кривых по стилю
- •9.1.2. Изменение стиля объектов
- •9.1.3. Настройка системных стилей точек и линий
- •Глава 10. Точки
- •10.1. Произвольная точка
- •10.2. Точки по кривой
- •10.3. Точки пересечений двух кривых
- •10.4. Все точки пересечений кривой
- •10.5. Точка на заданном расстоянии
- •Глава 11. Вспомогательные прямые
- •11.1. Произвольная прямая
- •11.1.1. Простановка точек пересечений
- •11.2. Горизонтальная прямая
- •11.3. Вертикальная прямая
- •11.4. Параллельная прямая
- •11.5. Перпендикулярная прямая
- •11.6. Касательная прямая через внешнюю точку
- •11.7. Касательная прямая через точку кривой
- •11.8. Прямая, касательная к двум кривым
- •11.9. Биссектриса
- •Глава 12. Отрезки
- •12.1. Отрезок
- •12.2. Параллельный отрезок
- •12.3. Перпендикулярный отрезок
- •12.4. Касательный отрезок из внешней точки
- •12.5. Касательный отрезок через точку кривой
- •12.6. Отрезок, касательный к двум кривым
- •Глава 13. Окружности
- •13.1. Окружность
- •13.1.1. Окружность с осями
- •13.2. Окружность по трем точкам
- •13.3. Окружность с центром на объекте
- •13.4. Окружность, касательная к кривой
- •13.5. Окружность, касательная к двум кривым
- •13.6. Окружность, касательная к трем кривым
- •13.7. Окружность по двум точкам
- •Глава 14. Эллипсы
- •14.1. Эллипс
- •14.2. Эллипс по диагонали габаритного прямоугольника
- •14.3. Эллипс по центру и вершине габаритного прямоугольника
- •14.4. Эллипс по центру, середине стороны и вершине описанного параллелограмма
- •14.5. Эллипс по трем вершинам описанного параллелограмма
- •14.6. Эллипс по центру и трем точкам
- •14.7. Эллипс, касательный к двум кривым
- •Глава 15. Дуги
- •15.1. Дуга
- •15.1.1. Выбор направления дуги
- •15.2. Дуга по трем точкам
- •15.3. Дуга, касательная к кривой
- •15.4. Дуга по двум точкам
- •15.5. Дуга по двум точкам и углу раствора
- •15.6. Дуги эллипсов
- •Глава 16. Многоугольники
- •16.1. Прямоугольник
- •16.2. Прямоугольник по центру и вершине
- •16.3. Многоугольник
- •Глава 17. Лекальные кривые
- •17.1. Ломаная
- •17.1.1. Замкнутые и разомкнутые кривые
- •17.1.2. Редактирование положения характерных точек
- •17.2. NURBS
- •17.3. Кривая Безье
- •Глава 18. Непрерывный ввод объектов
- •18.1. Создание объектов последовательности
- •18.2. Завершение ввода объектов
- •18.3. Стиль линии при непрерывном вводе объектов
- •Глава 19. Линия
- •19.1. Общий порядок построения объектов линии
- •19.2. Способы построения первого отрезка
- •19.2.1. Параллельно или перпендикулярно объекту
- •19.2.2. Касательно к объекту
- •19.2.3. Касательно к одному объекту и параллельно другому
- •19.2.4. Посередине между двумя параллельными прямыми
- •19.2.5. Касательно к двум объектам
- •19.2.6. На биссектрисе угла
- •19.3. Способы построения последующих отрезков
- •19.3.1. Параллельно или перпендикулярно объекту
- •19.3.2. Касательно к объекту
- •19.4. Способы построения первой дуги
- •19.4.1. Касательно к объекту
- •19.4.2. Произвольная
- •19.5. Способы построения последующих дуг
- •19.5.1. Касательно к объекту
- •19.5.2. По нормали к предыдущему сегменту
- •Глава 20. Штриховка
- •20.1. Задание границ штриховки
- •20.1.1. Ручное рисование границ
- •20.1.2. Обход границы по стрелке
- •20.2. Параметры штриховки
- •Глава 21. Составные объекты
- •21.1. Контур
- •21.2. Эквидистанта кривой
- •21.2.1. Параметры эквидистанты
- •21.3. Эквидистанта по стрелке
- •Глава 22. Фаски и скругления
- •22.1. Фаска
- •22.1.1. Управление усечением объектов
- •22.2. Фаска на углах объекта
- •22.3. Скругление
- •22.4. Скругление на углах объекта
- •Глава 23. Общие сведения о размерах
- •23.1. Настройка свойств
- •23.2. Настройка параметров
- •23.3. Управление размерной надписью
- •23.4. Выбор квалитета
- •23.5. Настройка размеров в текущем и новых документах
- •Глава 24. Линейные размеры
- •24.1. Простой линейный размер
- •24.1.1. Управление ориентацией размера
- •24.1.2. Указание объекта для простановки размера
- •24.1.3. Размер с наклонными выносными линиями
- •24.1.4. Формирование зазора между выносной линией и точкой привязки
- •24.2. Линейный размер с обрывом
- •24.3. Линейный размер от отрезка до точки
- •24.4. Линейный размер от общей базы
- •24.5. Цепной линейный размер
- •24.6. Линейный размер с общей размерной линией
- •24.7. Размер дуги
- •24.8. Размер высоты
- •24.8.1. Для вида спереди или разреза
- •Глава 25. Диаметральные и радиальные размеры
- •25.1. Диаметральный размер
- •25.2. Простой радиальный размер
- •25.3. Радиальный размер с изломом
- •Глава 26. Угловые размеры
- •26.1. Простой угловой размер
- •26.1.1. Управление ориентацией размера
- •26.2. Угловой размер от общей базы
- •26.3. Цепной угловой размер
- •26.4. Угловой размер с общей размерной линией
- •26.5. Угловой размер с обрывом
- •Глава 27. Авторазмеры
- •27.1. Линейный авторазмер
- •27.1.1. Способы управления размерной надписью авторазмера
- •27.2. Линейный авторазмер от отрезка до точки
- •27.3. Линейный авторазмер с обрывом
- •27.4. Угловой авторазмер
- •27.5. Угловой авторазмер с обрывом
- •27.6. Радиальный авторазмер
- •27.7. Диаметральный авторазмер
- •Глава 28. Обозначения ЕСКД
- •28.1. Общие сведения
- •28.3. Шероховатость
- •28.3.1. Ввод надписи обозначения шероховатости
- •28.3.2. Настройка отрисовки знака шероховатости
- •28.4.4. Изменение положения значка
- •28.5. Обозначение клеймения
- •28.5.1. Ввод надписи обозначения клеймения
- •28.5.2. Настройка отрисовки обозначения клеймения
- •28.6. Обозначение маркировки
- •28.7. Обозначение позиции
- •28.7.1. Ввод надписи обозначения позиции
- •28.7.2. Настройка отрисовки обозначения позиции
- •28.8. Обозначение изменения
- •28.8.1. Ввод надписи обозначения изменения
- •28.8.2. Настройка отрисовки обозначения изменения
- •28.9. Стрелка направления взгляда
- •28.9.1. Формирование текста обозначения
- •28.9.2. Автоматическое создание вида
- •28.9.3. Автосортировка буквенных обозначений
- •28.10. Линия разреза
- •28.10.1. Построение линии сложного разреза
- •28.11. Выносной элемент
- •28.11.1. Настройка отрисовки обозначения выносного элемента
- •28.12. База
- •28.12.1. Ввод надписи обозначения базы
- •28.13. Допуск формы
- •28.13.1. Формирование таблицы допуска
- •28.13.2. Создание ответвлений
- •28.14. Обозначение центра
- •28.14.1. Настройка отрисовки обозначения центра
- •28.15. Осевая линия
- •28.16. Автоосевая
- •28.16.1. Автоосевая по двум точкам
- •28.16.2. Построение автоосевой способом По объектам
- •28.16.3. Построение автоосевой способом C указанием границы
- •28.16.5. Пример использования автоосевой
- •28.17. Волнистая линия
- •28.17.1. Настройка параметров волнистой линии
- •28.17.2. Способы построения волнистой линии
- •28.17.3. Особенности редактирования волнистой линии
- •28.18. Линия с изломами
- •28.18.1. Настройка параметров линии с изломами
- •28.18.2. Смещение изломов
- •Глава 29. Обозначения СПДС
- •29.1. Общие сведения
- •29.2. Настройка обозначений СПДС в текущем и новых документах
- •29.3.1. Ввод текста марки/позиционного обозначения
- •29.3.2. Автонумерация марки/позиционного обозначения
- •29.3.4. Копирование свойств марок/позиционных обозначений
- •29.5. Марка/позиционное обозначение на линии
- •29.6. Обозначение узла
- •29.6.1. Ввод текста обозначения узла и узла в сечении
- •29.6.2. Параметры обозначения узла
- •29.7. Обозначение узла в сечении
- •29.7.1. Параметры обозначения узла в сечении
- •29.8. Номер узла
- •29.8.1. Ввод текста обозначения номера узла
- •29.9. Фигурная скобка
- •29.9.1. Ввод текста обозначения фигурной скобки
- •29.9.2. Параметры фигурной скобки
- •29.9.3. Особенности редактирования фигурной скобки с помощью мыши
- •29.10. Выносная надпись
- •29.10.1. Ввод текста выносной надписи
- •29.10.2. Параметры выносной надписи
- •29.11. Прямая координационная ось
- •29.11.1. Автопродолжение
- •29.11.2. Формирование обозначения
- •29.11.3. Параметры отрисовки
- •29.11.4. Выступы
- •29.11.5. Дополнительные обозначения
- •29.11.6. Параметры отрисовки дополнительных обозначений
- •29.11.7. Ввод текста дополнительных обозначений
- •29.12. Дуговая координационная ось
- •29.13. Круговая координационная ось
- •29.13.1. Параметры отрисовки
- •29.14. Использование команды «Запомнить состояние» для построения осей
- •29.14.1. Прямые оси
- •29.14.2. Дуговые оси
- •29.14.3. Круговые оси
- •Глава 30. Общие приемы редактирования
- •30.1. Редактирование объектов с помощью мыши
- •30.1.1. Перемещение
- •30.1.2. Копирование
- •30.2. Редактирование характерных точек
- •30.2.1. Перемещение характерной точки мышью
- •30.2.2. Перемещение характерной точки при помощи клавиатуры
- •30.2.3. Перемещение характерной точки с осуществлением привязки
- •30.2.4. Задание координат характерной точки
- •30.2.5. Удаление характерной точки
- •Глава 31. Сдвиг
- •31.1. Произвольный сдвиг
- •31.1.1. Управление исходными объектами
- •31.2. Сдвиг по углу и расстоянию
- •Глава 32. Копирование
- •32.1. Произвольная копия
- •32.1.1. Масштаб и поворот копий
- •32.1.2. Управление атрибутами при копировании
- •32.2. Копия по кривой
- •32.2.1. Интерпретация шага
- •32.2.2. Расположение копий
- •32.2.3. Направление копирования
- •32.3. Копия по параллелограммной сетке
- •32.4. Копия по концентрической сетке
- •32.4.1. Расположение копий
- •32.5. Копия по окружности
- •Глава 33. Преобразования объектов
- •33.1. Поворот
- •33.2. Масштабирование
- •33.2.1. Управление масштабированием выносных линий
- •33.3. Симметрия
- •33.3.1. Указание существующей оси симметрии
- •33.4. Преобразование в NURBS
- •Глава 34. Деформация
- •34.1. Выбор объектов для деформации
- •34.2. Деформация сдвигом
- •34.3. Деформация поворотом
- •34.4. Деформация масштабированием
- •Глава 35. Разбиение объектов на части
- •35.1. Разбить кривую на две части
- •35.2. Разбить кривую на несколько равных частей
- •Глава 36. Удаление частей объектов
- •36.1. Усечение кривых
- •36.2. Усечение кривых по указанным точкам
- •36.3. Выравнивание по границе
- •36.4. Удаление фасок и скруглений
- •36.5. Очистка области
- •36.6. Удаление частей объектов оформления и библиотечных макроэлементов
- •36.7. Очистка фона
- •Глава 37. Удаление объектов
- •37.1. Удаление вспомогательных объектов
- •37.2. Удаление всех объектов документа
- •37.3. Удаление объектов оформления
- •Глава 38. Именованные группы
- •38.1. Создание новой группы
- •38.2. Добавление объектов в группу
- •38.3. Исключение объектов из группы
- •38.4. Выделение группы
- •38.5. Разрушение группы
- •Глава 39. Использование макроэлементов
- •39.1. Создание нового макроэлемента
- •39.2. Выделение макроэлемента
- •39.3. Разрушение макроэлемента
- •Глава 40. Использование растровых изображений
- •40.1. Вставка
- •40.2. Редактирование
- •40.2.1. Настройка редактирования растровых объектов, взятых в документ
Глава 14. Эллипсы
При построении эллипсов с помощью всех нижеописанных команд управление отрисов! кой осевых линий производится так же, как при создании окружностей (см. раз! дел 13.1.1 на с. 123).
14.1.Эллипс
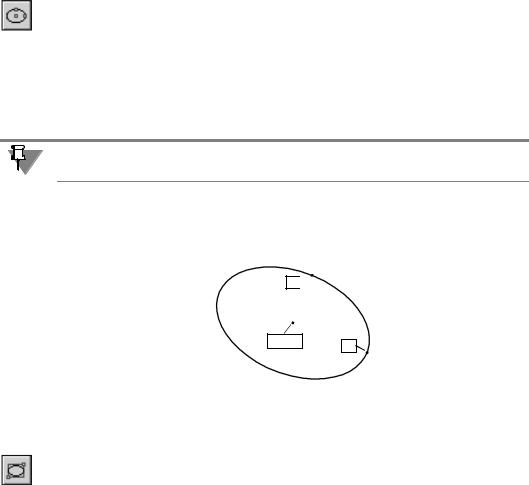
Чтобы построить произвольный эллипс, вызовите команду Эллипс.
Укажите центральную точку эллипса.
Задайте величину первой полуоси эллипса. Это можно сделать двумя способами.
▼задайте конечную точку полуоси т1,
▼введите длину полуоси в соответствующем поле на Панели свойств.
Угол наклона первой полуоси к оси абсцисс текущей системы координат определяется автоматически.
Если необходимо, перед указанием величины первой полуоси вы можете задать точное значение угла ее наклона в соответствующем поле Панели свойств.
Задайте величину второй полуоси эллипса. Это тоже можно сделать двумя способами.
▼задайте конечную точку полуоси т2,
▼введите длину полуоси в соответствующем поле на Панели свойств.
т1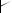
Центр |
т2 |
|
Рис. 14.1. Эллипс по центру и размерам полуосей
14.2.Эллипс по диагонали габаритного прямоугольника
Чтобы построить эллипс, вписанный в прямоугольник с заданной диагональю, вызовите команду Эллипс по диагонали прямоугольника.
Введите в соответствующее поле на Панели свойств величину угла наклона первой полу! оси эллипса к оси абсцисс текущей системы координат (по умолчанию она равна 0°).
Затем задайте начальную (т1) и конечную (т2) точки диагонали прямоугольника, описан! ного вокруг создаваемого эллипса. Длины полуосей эллипса будут рассчитаны автома! тически.
128
Глава 14. Эллипсы
т2
т1
Рис. 14.2. Эллипс по диагонали габаритного прямоугольника
14.3.Эллипс по центру и вершине габаритного прямоугольника
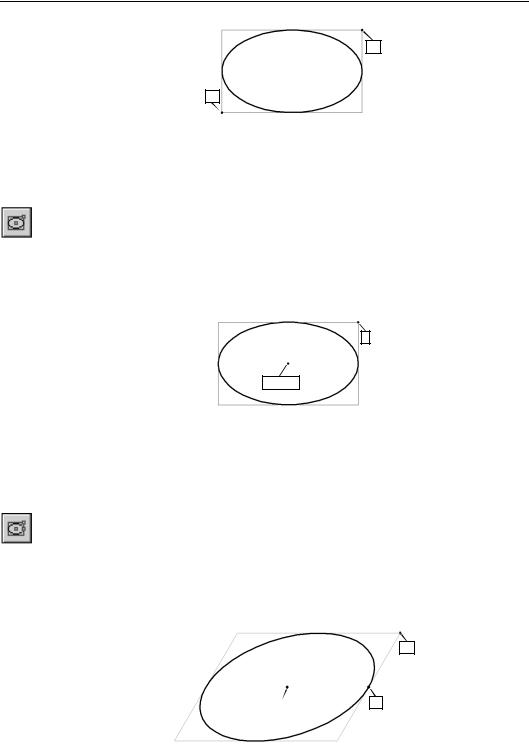
Чтобы построить эллипс, вписанный в прямоугольник с заданным центром и вершиной, вызовите команду Эллипс по центру и вершине прямоугольника.
Введите в соответствующее поле на Панели свойств величину угла наклона первой полу! оси эллипса к оси абсцисс текущей системы координат (по умолчанию она равна 0°).
Затем задайте центральную точку и вершину прямоугольника, описанного вокруг созда! ваемого эллипса. Длины полуосей эллипса будут рассчитаны автоматически.
т
Центр
Рис. 14.3. Эллипс по центру и вершине габаритного прямоугольника
14.4.Эллипс по центру, середине стороны и вершине описанного параллелограмма
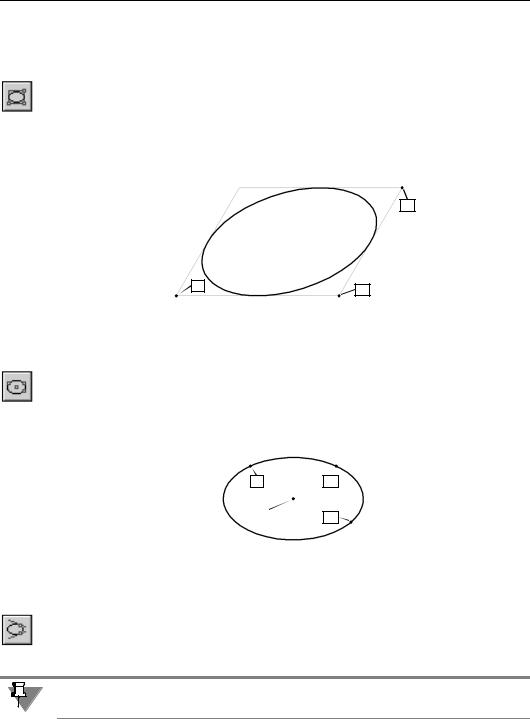
Чтобы построить эллипс, вписанный в параллелограмм с заданным центром, серединой стороны и вершиной, вызовите команду Эллипс по центру, середине стороны и вер шине параллелограмма.
Задайте точку точки центра, затем середину стороны (т1) и вершину (т2) параллелограм! ма, описанного вокруг создаваемого эллипса.
Длины полуосей эллипса и угол наклона его первой полуоси к оси абсцисс текущей сис! темы координат будут рассчитаны автоматически.
т2
Центр |
т1 |
Рис. 14.4. Эллипс по центру, середине стороны и вершине параллелограмма
129
Часть III. Геометрические объекты
14.5.Эллипс по трем вершинам описанного параллелограмма
Чтобы построить эллипс, вписанный в параллелограмм с тремя заданными вершинами, вызовите команду Эллипс по 3 вершинам параллелограмма.
Задайте положения вершин т1, т2 и т3 параллелограмма, описанного вокруг создавае! мого эллипса.
Длины полуосей эллипса и угол наклона его первой полуоси к оси абсцисс текущей сис! темы координат будут рассчитаны автоматически.
т3
т1 |
т2 |
|
Рис. 14.5. Эллипс по трем вершинам габаритного параллелограмма
14.6.Эллипс по центру и трем точкам
Чтобы построить эллипс с определенным центром и проходящий через три заданные точки, вызовите команду Эллипс по центру и 3 точкам.
Укажите положение центральной точки создаваемого эллипса, а затем точки т1, т2 и т3, принадлежащие ему.
т1 т2
Центр |
т3 |
Рис. 14.6. Эллипс по центру и трем точкам
14.7.Эллипс, касательный к двум кривым
Чтобы построить эллипс, касательный к двум заданным объектам, вызовите команду
Эллипс, касательный к 2 кривым.
Укажите первый и второй объекты в точках т1 и т2 их касания с эллипсом.
Для точного позиционирования курсора воспользуйтесь клавиатурными привязками (см. табл. 8.5 на с. 82).
Задайте точку т3, через которую должен проходить создаваемый эллипс.
130

Глава 14. Эллипсы
т1
 т2
т2
т3
Рис. 14.7. Эллипс, касательный к отрезку и окружности
131
