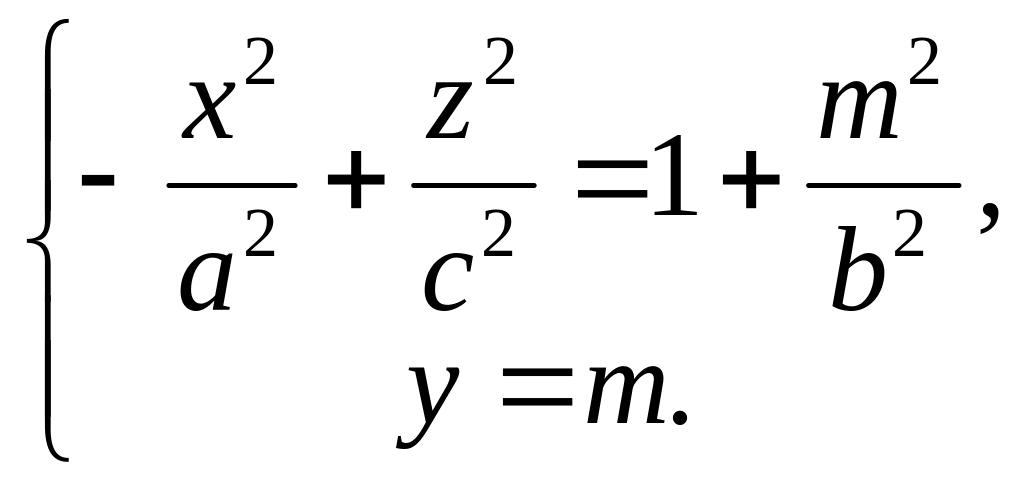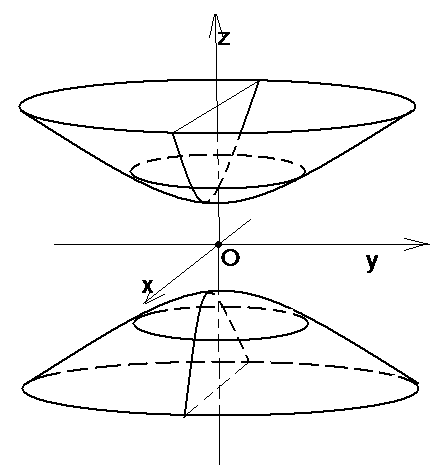
4.3.6. Двуполостный гиперболоид

Определение 15. Двуполостным гиперболоидом называется множество точек пространства, которое в некоторой прямоугольной системе координат можно задать уравнением

(32)

Из уравнения (32) следует

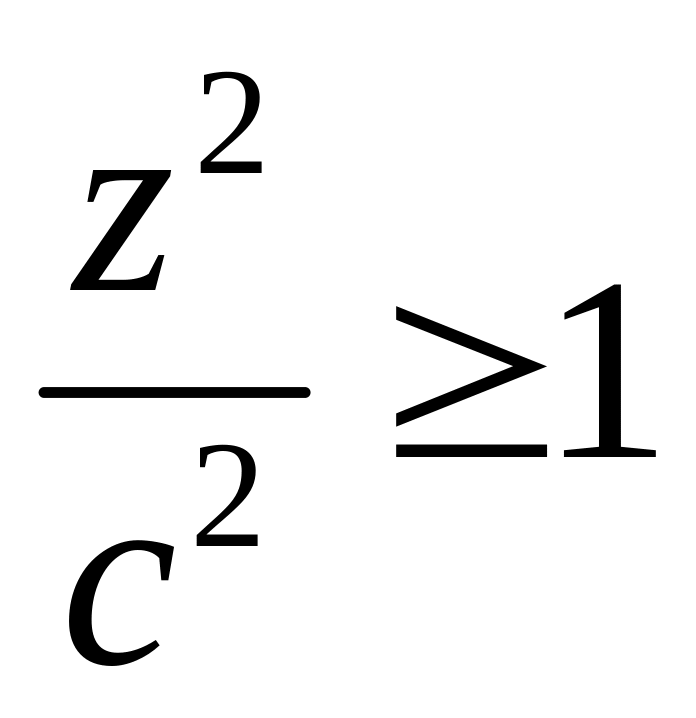• , т.е. гиперболоид лежит вне полосы, ограниченной плоскостями z =  с.

• Однополостный гиперболоид симметричен относительно координатных плоскостей, координатных осей и начала координат.

Исследуем форму этого гиперболоида методом сечений.

I. Пересечём гиперболоид плоскостью, параллельной (ХОУ), её уравнение z = h. Уравнения

сечения (). Как отмечено выше, плоскости z = h при с  h  с не пересекают гиперболоид. При h  с в сечении получается эллипс с полуосями и . Эти полуоси неограниченно возрастают при увеличении h. II. При пересечении гиперболоида плоскостями у = m, параллельными плоскости (ХОZ) получаются линии

Рис. 25

Эти уравнения определяют гиперболы, полуоси которых возрастают при увеличении m.

III. При пересечении гиперболоида плоскостями, параллельными плоскости (УОZ) получаются тоже гиперболы Исследуйте этот случай сами) (рис. 25).

ЭЛЛИПТИЧЕСКИЙ ПАРАБОЛОИД

Определение 16. Эллиптическим параболоидом называется множество точек пространства, которое в некоторой прямоугольной системе координат можно задать уравнением (33).

Из уравнения (33) следует:

• z  0, т.е. параболоид лежит целиком в одной полуплоскости с границей (ХОУ), а именно в той, в которой лежит положительная полуось ОZ;

• параболоид симметричен относительно плоскостей (ХОZ), (УОZ) и оси (ОZ).

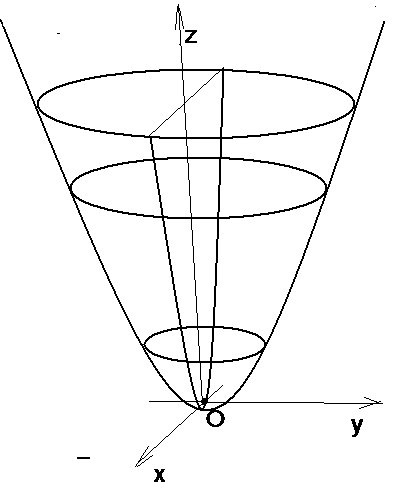
Исследуем параболоид методом сечений. Очевидно плоскости z = h могут пересекать параболоид только при h  0. при этом в сечениях будут получаться эллипсы с полуосями

и , если h  0. Эти полуоси неограниченно возрастают при увеличении h. При h = 0 в сечении будет одна точка – начало координат. Плоскости, параллельные плоскостям (ХОZ) и (УОZ), пересекают параболоид по параболам (исследуйте эти сечения самостоятельно) (рис. 26).

Рис. 26

4.3.7. Гиперболический параболоид

Определение 17. Гиперболическим параболоидом называется множество точек пространства, которое в некоторой прямоугольной системе координат можно задать уравнением (34).

Из уравнения (34) следует, что параболоид симметричен относительно плоскостей (ХОZ), (УОZ) и оси (ОZ).

Исследуем параболоид методом сечений.

I. При пересечении параболоида плоскостями z = h, параллельными плоскости (ХОУ), получаются линии ()

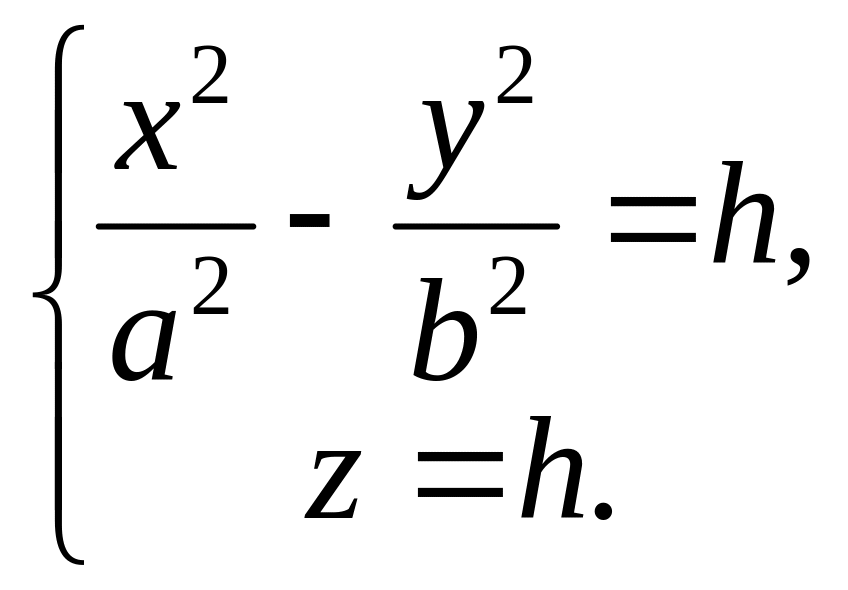При h  0 в сечении получаются гиперболы, действительные оси которых параллельны оси (ОУ), при h  0 гиперболы с действительными осями, параллельными оси (ОХ). При h = 0 плоскость (ХОУ) пересекает параболоид по паре пересекающихся прямых.

II. В сечении плоскостями у = m, параллельными плоскости (ХОZ) получаются параболы у = m, оси которых параллельны оси (ОZ), ветви направлении в направлении оси (ОZ) и вершинами являются точки (0, m, ).

III. В сечении плоскостями х = n, параллельными плоскости (УОZ), получаются линии 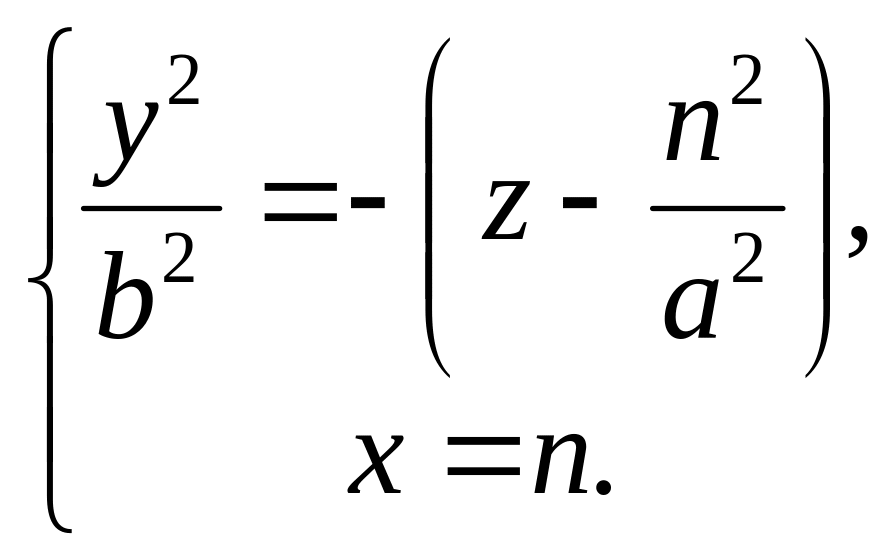Эти уравнения определяют параболы, оси которых параллельны оси (ОZ), ветви направлении в направлении, противоположном оси (ОZ), и вершинами являются точки (n, 0, ).

Исследование методом сечений даёт следующую поверхность
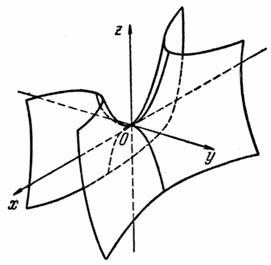
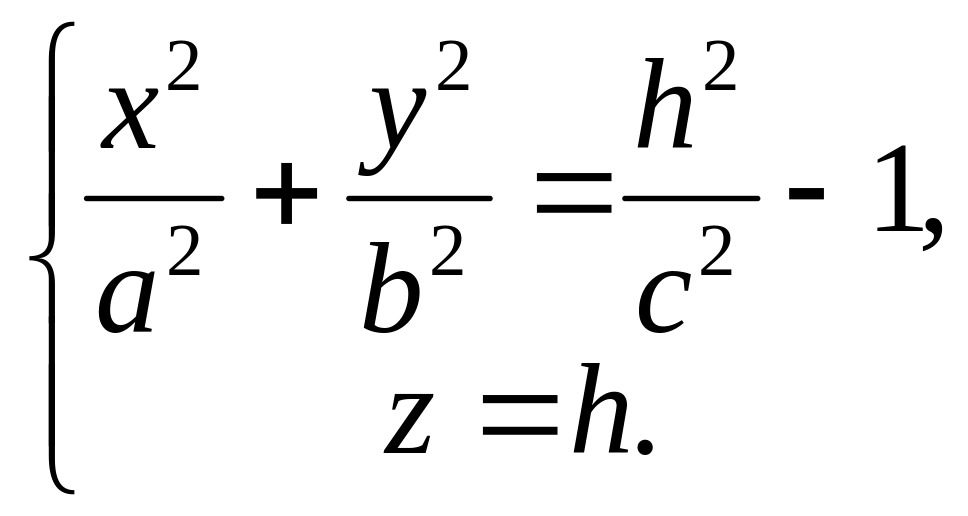