2.2.3. Общие уравнения прямой

Из уравнений (16) и (18) видно, что любую прямую на плоскости можно задать уравнением первой степени с двумя переменными. Возникает обратный вопрос: всякое ли уравнение первой степени с двумя переменными задаёт в аффинной системе координат на плоскости некоторую прямую? Аналогично, уравнения (16¹) и (18¹) эквивалентны системе двух независимых уравнений первой степени с тремя переменными. Поэтому возникает обратная задача: Любая ли система двух независимых уравнений первой степени с тремя переменными задаёт в аффинной системе координат в пространстве прямую?

I.Общее уравнение прямой на плоскости

Дано: R = и уравнение Ах + Ву + С = 0, где из коэффициентов А и В хотя бы один отличен от нуля.

Показать, что данное уравнение определяет прямую.

Доказательство. Пусть В  0. При х₀ = 0 из данного уравнения получаем у₀ = . Вектор не нулевой, поэтому существует и только одна прямая l такая, что l  М₀, где М₀(х₀, у₀) и l  . Запишем уравнение l, используя (16). Получим 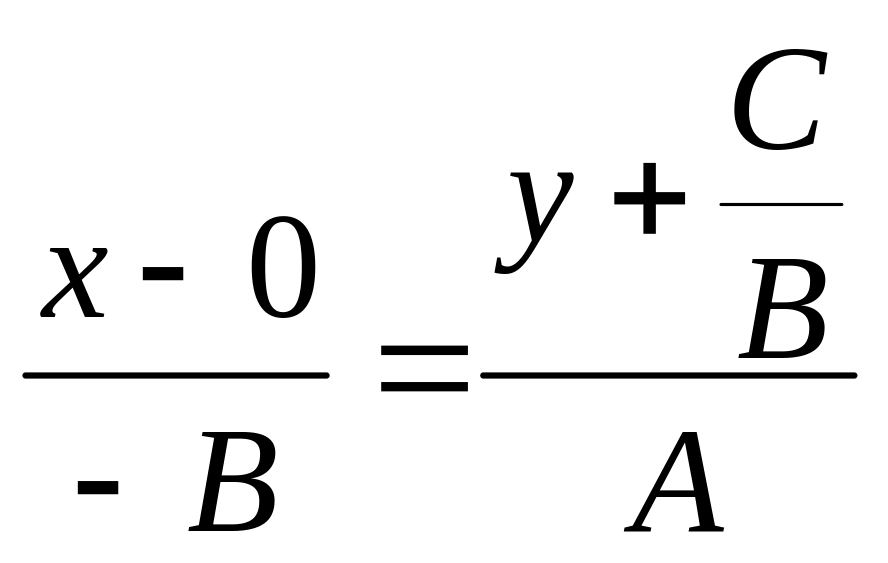. После преобразования Ах + Ву + С = 0. Получили данное уравнение. Следовательно, оно задаёт прямую.

Уравнение Ах + Ву + С = 0 называется общее уравнение прямой на плоскости. При этом из доказательства следует, что вектор параллелен этой прямой.

II. Общие уравнения прямой в пространстве

Дано: R = и система (19), где коэффициенты А₁, В₁, С₁ не пропорциональны коэффициентам А₂, В₂, С₂ .

Показать, что данная система определяет прямую.

Доказательство. Пусть (х₀, у₀, z₀) – одно из решений данной системы, т.е. Вычтем из данной системы почленно полученные тождества. Получим систему (), эквивалентную данной. Это система двух линейных однородных уравнений с тремя переменными. Так как её коэффициенты не пропорциональны, то эта система имеет бесконечно много решений, причём все решения пропорциональны. Следовательно, достаточно найти одно ненулевое решение. Таким решением будет тройка . Проверим это подстановкой. Подставим в первое уравнение: Подставим во второе уравнение: Итак, тройка удовлетворяет обоим уравнениям системы (). Эта тройка не нулевая. Следовательно, все решения системы () можно записать в виде

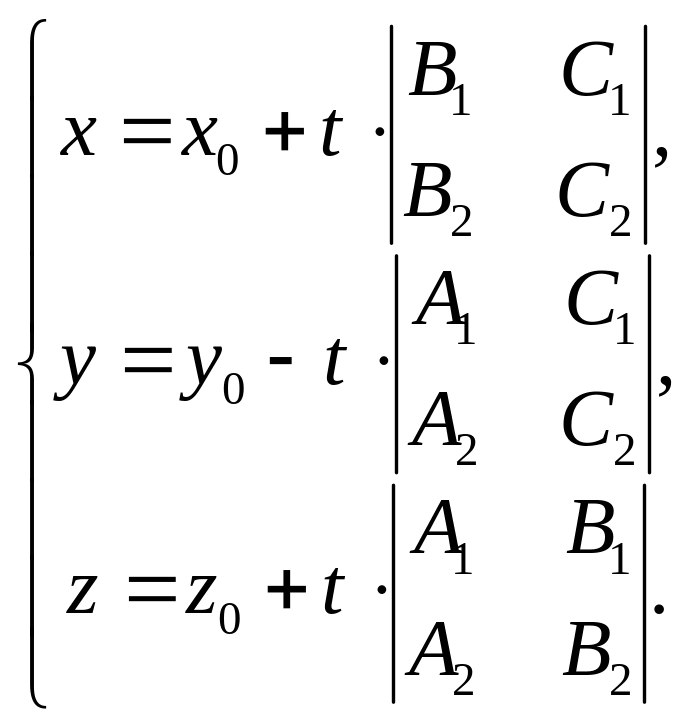или (20)

Итак, система эквивалентна системе (20). Но система (20) это параметрические уравнения прямой. Следовательно, уравнения (19) задают прямую в аффинной системе координат в пространстве.

Уравнения (19) называются общие уравнения прямой в пространстве. Если прямая задана уравнениями (19), то вектор = параллелен данной прямой.

Замечание. Если прямая в пространстве задана общими уравнениями, то для приведения их к параметрическому (или каноническому виду) достаточно найти одно решение (х₀, у₀, z₀) этих уравнений, найти вектор и использовать уравнение (20) или .

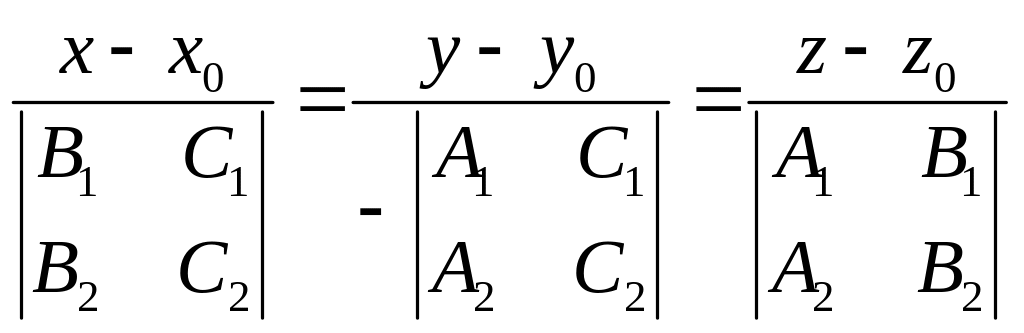2.2.4. Исследование взаимного расположения прямых

I. Исследовать взаимное расположение прямых, заданных общими уравнениями в АСК на плоскости.

Дано. R = , l₁ : A₁x + B₁y + C₁ = 0, l₂ : A₂x + B₂y + C₂ = 0.

Исследовать взаимное расположение l₁ и l₂ .

Исследование. Взаимное расположение прямых на плоскости зависит от числа их общих точек. Точка является общей для двух прямых тогда и только тогда, когда её координаты удовлетворяют уравнениям обеих прямых, т.е. удовлетворяют системе уравнений

(21)

Таким образом геометрическая задача сведена к алгебраической – к исследованию системы двух уравнений с двумя неизвестными. Из курса алгебры известно, что для такой системы возможны три случая.

1. . В этом случае система (21) имеет единственное решение. На геометрическом языке это означает, что прямые l₁ и l₂ имеют одну общую точку, т.е. пересекаются. Итак, условие есть условие пересечения прямых, заданных общими уравнениями.

2. . В этом случае уравнения системы (21) эквивалентны, т.е. все решения одного из них являются решениями другого. На геометрическом языке – все точки одной прямой лежат на другой, т.е. прямые совпадают.

3. . В этом случае система (21) не имеет ни одного решения. На геометрическом языке – прямые l₁ и l₂ не имеют ни одной общей точки.

Если вспомнить определение: прямые l₁ и l₂ называются параллельными, если они лежат в одной плоскости и либо совпадают, либо не имеют ни одной общей точки, то получаем, что прямые l₁ и l₂ параллельны тогда и только тогда, когда .

II. Исследовать взаимное расположение прямых на плоскости в АСК, если одна из прямых задана общим уравнением, а вторая – параметрическими уравнениями.

Дано. R = , l₁ : Ax + By + C = 0, l₂ :

Исследовать взаимное расположение l₁ и l₂ .

Исследование. Взаимное расположение прямых на плоскости зависит от числа их общих точек. Точка является общей для двух прямых тогда и только тогда, когда её координаты удовлетворяют уравнениям обеих прямых, т.е. удовлетворяют системе уравнений

(22)

Подставив выражения х и у в первое уравнение и приведя подобные, получим

t(Am + Bn) + (Ax₀ + By₀ + C) = 0 (23)

Для уравнения (23) возможны три случая.

1. Am + Bn  0. В этом случае Уравнение (23) имеет одно решение. На геометрическом языке это значит, что l₁ и l₂ имеют одну общую точку. Получили условие пересечения прямых.

2. Am + Bn = 0 и Ax₀ + By₀ + C = 0. В этом случае уравнение (23) имеет вид 0t + 0 = 0. Этому уравнению удовлетворяют все t  R. На геометрическом языке это значит, что все точки второй прямой принадлежат первой прямой, т.е. прямые совпадают.

3. Am + Bn = 0, но Ax₀ + By₀ + C  0. Уравнение (23) не имеет решения. Следовательно, прямые l₁ и l₂ не имеют ни одной общей точки.

Из случаев 2 и 3 получаем: прямые l₁ и l₂ параллельны тогда и только тогда, когда Am + Bn = 0.

III. Исследовать взаимное расположение двух прямых в АСК в пространстве, если прямые заданы параметрическими (или каноническими) уравнениями.

Дано: R = , , : .

Исследовать взаимное расположение l₁ и l₂ .

Исследование. Из уравнений первой прямой М₁(х₁, у₁, z₁)  l₁, , l₁. Из

уравнений второй прямой М2(х2, у2, z2)  l2, , l2. Возможны следующие случаи. 1. l1l2    . 2. l1= l2   и М1  l2  и

Рис. 19

.

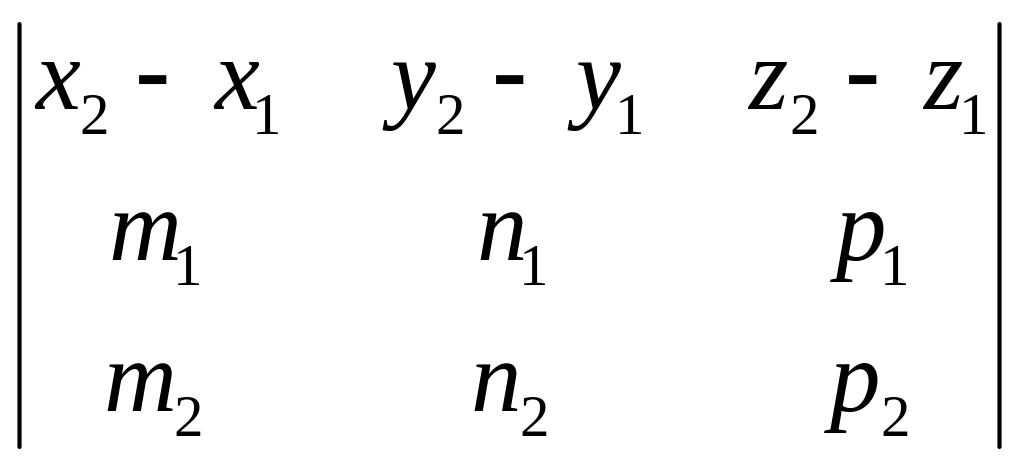3. l₁ пересекает l₂  векторы компланарны  = 0.

4. l₁ скрещивается с l₂  векторы не компланарны   0.