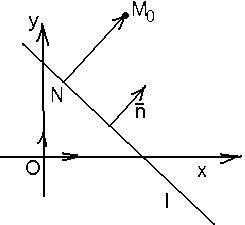2.3.6. Расстояние от точки до прямой

Дано: R = , l : Ax + By + C = 0, М0(х0, у0). Найти d (M0, l ). Решение. Опустим из точки М0 на данную прямую перпендикуляр. Пусть N – его основание и N(х1,у1). Тогда Ax1 + By1 + C = 0 (). Искомое расстояние d (M0, l ) = . Если , то . Следовательно, векторы и коллинеарны. Так как , то (). Отсюда следует

Рис. 26

d (M₀, l ) = = . ()

Для решения задачи достаточно найти . Для этого обе части равенства () умножим скалярно на вектор , получим . Полученное равенство перепишем в координатах: А(х₀  х₁) + В(у₀  у₁) =  (А² + В²). Отсюда Ах₀ + Ву₀  (Ах₁ + Ву₁) =  (А² + В²). Из () Ах₁ + Ву₁ = С. Следовательно, Ах₀ + Ву₀ + С =  (А² + В²) и . Подставив в (), получим d (M₀, l ) = (35)

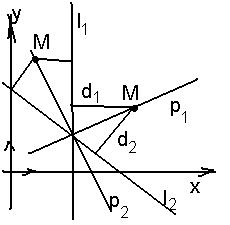
Задача. Дано: R = , l1 : 3х + 4у +12 = 0, l2 : 4х + 3у  24 = 0. Найти уравнения биссектрис углов, образованных l1 и l2. Решение. Пусть р1 и р2 – искомые биссектрисы. Тогда М  р1 или р2  d1 = d2, где d1 = d (M, l1), d2 = d (M, l2 ). Используя формулу (35), получим М  р1 или р2  .

Рис.27

После упрощения получим два уравнения:

р₁ : х  у  36 = 0; р₂ : 7х + 7у  12 = 0.

(Сравните с решением и результатом предыдущей задачи).

2.4. Пучок прямых на плоскости

Определение 24. Пучком прямых на плоскости называется множество всех прямых этой плоскости, проходящих через одну точку. Эта точка называется центром пучка.

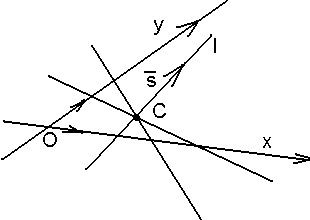
Пучок можно задать двумя способами: центром и парой пересекающихся прямых. I. Пучок задан центром. Дано. R = , С(х0, у0) – центр пучка (рис. 28). Найти условие, определяющее пучок. Решение. Прямая l принадлежит пучку с центром С тогда и

Рис. 28

только тогда, когда l  С. При этом направляющим вектором может быть любой ненулевой вектор . Следовательно, l принадлежит пучку  l : , где m, n – любые действительные числа, не равные одновременно нулю. Итак, пучок с центром С задаётся уравнением (36).

В уравнении (36) две пары переменных. Меняя m, n, мы будем получать все возможные прямые пучка. Если m, n зафиксированы, то зафиксирована прямая пучка. При этом, меняя х, у, мы будем получать все возможные точки на полученной прямой.

II. Пучок задан парой пересекающихся прямых. Дано. R = , l1 : A1x + B1y + C1 = 0, l2 : A2x + B2y + C2 = 0 (рис. 29). Найти уравнение пучка. Решение. Пусть l1  l2 = С и С(х0, у0). Точка С будет центром пучка. Используя уравнение (36) получим, что прямая l принадлежит пучку  l : . Здесь

Рис. 29

вектор  любой ненулевой вектор. Из уравнений прямых l₁ и l₂ векторы и параллельны прямым l₁ и l₂ соответственно, поэтому они не коллинеарны. Следовательно, любой вектор , где ,  - любые действительные числа, не равные нулю одновременно. Отсюда . Уравнение (36) перепишется . После преобразования получим:

().

Так как С = l₁  l₂, то A₁x₀ + B₁y₀ + C₁ = 0 и A₂x₀ + B₂y₀ + C₂ = 0. Отсюда ( A₁x₀ + B₁y₀) = С₁, ( A₂x₀ + B₂y₀) = 0. Подставив в (), получим уравнение данного пучка

(37)

В уравнении (37) тоже две пары переменных (, ) и (х, у).

Задача. Дано: R = , l₁ : 3х + 4у +12 = 0, l₂ : 4х + 3у  24 = 0, l₃ : х + 2у + 3 = 0.

Найти уравнение прямой l, Если l  (l₁  l₂) и l  l₃.

Решение. Так как l  (l₁  l₂), то l принадлежит пучку прямых, определяемому прямыми l₁ и l₂. Следовательно, уравнение l можно искать в виде

(3х + 4у +12 ) + (4х + 3у  24) = 0 ()

Преобразовав это уравнение, получим (3 + 4)х + (4 +3)у + (12  24) = 0 ().

Используем условие перпендикулярности прямых (33). Получим 1(3 + 4) + 2(4 +3) = 0, или 11 + 10 = 0. Так как все решения этого уравнения пропорциональны, а уравнение () при пропорциональных парах (, ) задаёт одну и ту же прямую, то достаточно найти одну ненулевую пару (, ). При  = 10  = 11. Подставив в (), получим уравнение

l : 14х  4у  384 = 0.

2.5. Геометрический смысл неравенств Ах + Ву + С  0 ( 0, 0,  0)

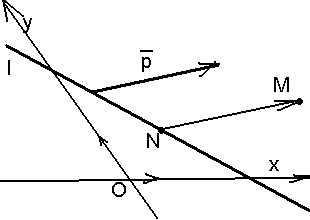
Дано. R = , Ах + Ву + С  0 (А и В н равны нулю одновременно) (38).

Исследовать, какую фигуру задаёт неравенство (38). Решение. Пусть l : Ах + Ву + С = 0. Если бы вектор был параллелен прямой l, то векторы и были бы коллинеарны. Но тогда . Отсюда А2 + В2 = 0, т.е.

Рис. 30

А = В = 0, что противоречит условию. Итак, вектор не параллелен прямой (рис.30).

Рассмотрим множество всех точек плоскости, не лежащих на прямой l. Пусть М – любая из них. Пусть параллелен , где N  l. Тогда = . При этом   0  точки М лежат в одной открытой полуплоскости с границей l, а именно в той в сторону которой направлен вектор . Перепишем последнее равенство в координатах. Если М (х, у), N (х₀ , у₀), то х  х₀ = А, у  у₀ = В. Отсюда х₀ = х  А, у₀ = у  В. Так как N  l, то Ах₀ + Ву₀ + С = 0. Следовательно, А(х  А) + В(у  В) + С = 0. Отсюда Ах + Ву + С =  (А² + В²). Так как А² + В²  0, то знак трёхчлена Ах + Ву + С совпадает со знаком  . Итак, Ах + Ву + С  0  точка М (х, у) лежит в открытой полуплоскости с границей l, а именно в той в сторону которой направлен вектор . Неравенство Ах + Ву + С  0 задаёт эту полуплоскость вместе с границей.