4.3.2. Конические поверхности

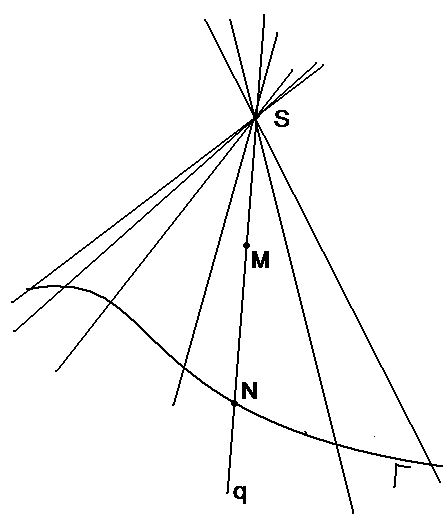
Определение 11. Конической поверхностью с направляющей Г и вершиной S (S и Г не лежат в одной плоскости) называется множество точек всех возможных прямых, проходящих через S и пересекающих Г.

Коническую поверхность обозначим К. Прямые , на которых лежат все точки К, называются образующими.

Пусть в пространстве зафиксирована система аффинных координат, S(х0, у0, z0), Г: М  К  М лежит хотя бы на одной из образующих. Пусть М q. Каждая образующая пересекает линию Г. Пусть Г  q = N (рис. 19). Если N(х1, у1, z1), то () Прямая q проходит через две точки, N и S, М  q  х = х0 + (х1 – х0)t, у = у0 + (у1 – у0)t, z = z0 + (z1  z0)t, tR. И этих равенств х1 = , у1 = , .

Рис. 19

Подставив х₁, у₁, z₁ в систему (), получим уравнения данной конической поверхности, но эти уравнения содержат параметр t. Для того, чтобы получить общее уравнение К, нужно из полученной системы исключить параметр t.

Получили следующие правила для составления уравнения конической поверхности:

Для составления уравнения поверхности К достаточно в уравнениях направляющей заменить х на , у на , z на и из полученной системы исключить параметр t.

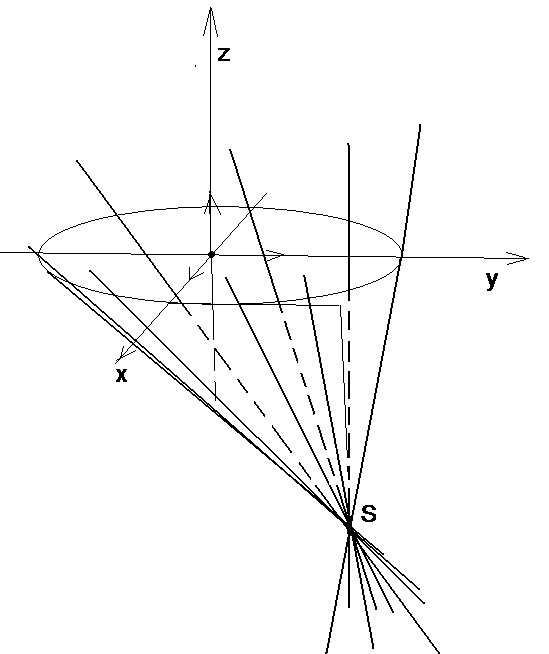
Пример 3. Найдите уравнение конической поверхности с вершиной S(2, 2, 3), если

направляющей является эллипс , z = 0. Решение. В уравнениях эллипса заменим х на , у на , z на . Получим , = 0. Найдём из второго уравнения t, получим t = . Подставив в первое уравнение, получим

Рис.20

81х² +36у²  272z² +108хz  48уz  288у  1752 z  2340 =0.

Замечание. Если направляющей является линия второго порядка, то полученная поверхность называется конусом второго порядка. Можно показать, что для любого конуса второго порядка можно в качестве направляющей взять эллипс, поэтому конус второго порядка называют эллиптическим конусом.

4.3.3. Поверхности вращения

Пусть даны линия Г и прямая р.

Определение 12. Поверхностью, полученной вращением линии Г вокруг оси р, называется множество точек всех возможных окружностей, лежащих в плоскостях, перпендикулярных р, центры которых лежат на р и которые пересекают линию Г.

Выведем уравнение поверхности вращения в том случае, когда Г и р лежат в одной плоскости ( обозначим эту плоскость П). Выберем прямоугольную систему координат, направив ось (ОХ) по оси р, ось (ОУ) – в плоскости П, тогда ось (ОZ) будет перпендикулярна П.

Так как линия Г лежит в плоскости (ХОУ), то в этой плоскости она задаётся некоторым уравнением f(х, у) = 0 ().

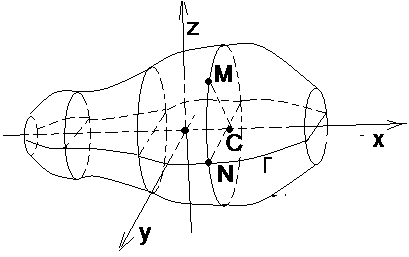
Пусть М(х, у, z) – произвольная точка. Тогда М  поверхности вращения  М  , где  - окружность, центр С которой лежит на оси (ОХ), её плоскость перпендикулярна оси (ОХ) и радиус равен NС (N  Г). Тогда точка С(х, 0, 0), N(х, у1, 0), NС = у1, МС= . Следовательно, М     у1 =  . Так как N  Г, то f(х, у1) = 0. Подставив значение у1,

Рис. 21

получим f(х,  ) = 0 (29). Это и есть уравнение данной поверхности вращения. Итак, получили следующее правило:

Если линия Г лежит в плоскости (ХОУ) и ось вращения совпадает с осью (ОХ), то для того, чтобы получить уравнение поверхности вращения, достаточно в уравнении линии Г координату х оставить без изменения, а у заменить на  .

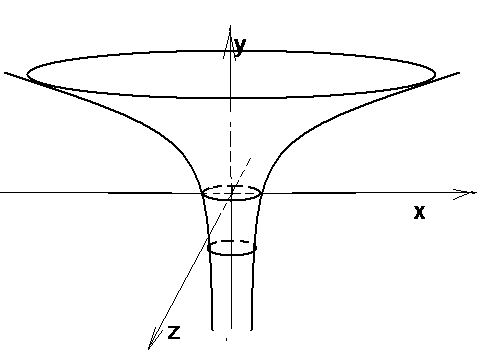
Пример 4. Написать уравнение поверхности, образованной вращением линии у = logx вокруг оси (ОУ).

Решение. Так как линия Г лежит в плоскости (ХОУ) и осью вращения является ось (ОУ) то в уравнении у = logx нужно у оставить без изменения, а х заменить на . Так как логарифм отрицательного числа не существует, то х заменяем на . Получим уравнение .

Рис. 22