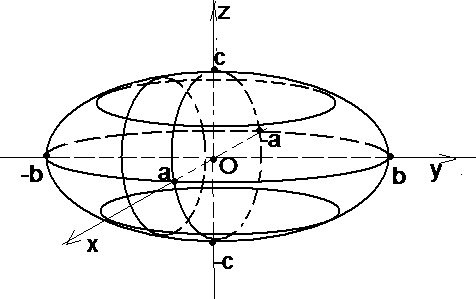
4.3.4. Эллипсоид

Определение 13. Эллипсоидом называется множество точек пространства, которое в некоторой прямоугольной системе координат можно задать уравнением

(30)

Из уравнения сразу следуют такие свойства эллипсоида:

• а  х  а, b  у  b, с  z  с. Следовательно, эллипсоид лежит внутри прямоугольного параллелепипеда, симметричного относительно координатных плоскостей, длины рёбер которого равны 2а, 2b, 2с;

• Эллипсоид симметричен относительно координатных плоскостей, координатных осей и начала координат.

Исследуем форму эллипсоида.

Если поверхность задана уравнением, то исследование её формы часто бывает удобно проводить методом сечений. Для этого исследуемую поверхность пересекают различными плоскостями, проще всего координатными и параллельными координатным.

I. Пересечём эллипсоид плоскостью, параллельной (ХОУ), её уравнение z = h. Уравнения сечения будут ()

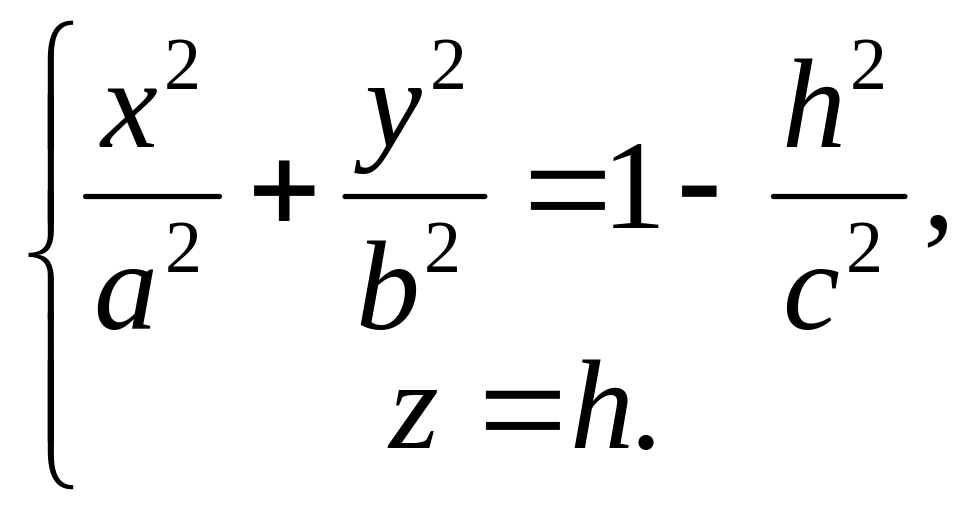Возможны случаи:

1) с  h  с. В этом случае система () определяет эллипс в плоскости z = h. Полуоси эллипса равны а и b . Наибольшие полуоси получаются при h = 0, т.е. в плоскости (ХОУ). При h   с полуоси стремятся к нулю, т.е. эллипс стягивается в точку. 2) h =  с. В каждой из этих плоскостей система () определяет точку, т.е. плоскости z =  с пересекают эллипсоид в одной точке каждая (рис.23).

Рис. 23

3) h  с или h  с. В этом случае система () определяет пустое множество точек, т.е. плоскости z = h при указанных h не пересекают эллипсоид.

II. При пересечении эллипсоида плоскостями, параллельными (ХОZ) и (УОZ) получим аналогичные результаты. Проведите эти исследования самостоятельно.

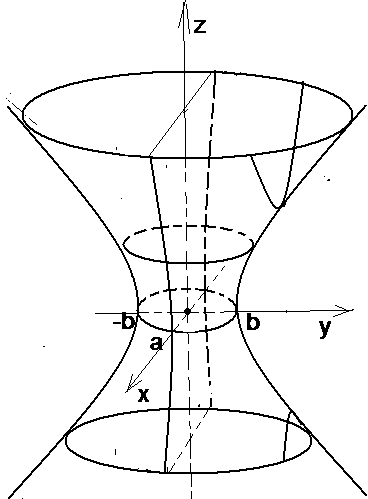
4.3.5. Однополостный гиперболоид

Определение 14. Однополостным гиперболоидом называется множество точек пространства, которое в некоторой прямоугольной системе координат можно задать уравнением

(31)

Из уравнения (31) следует

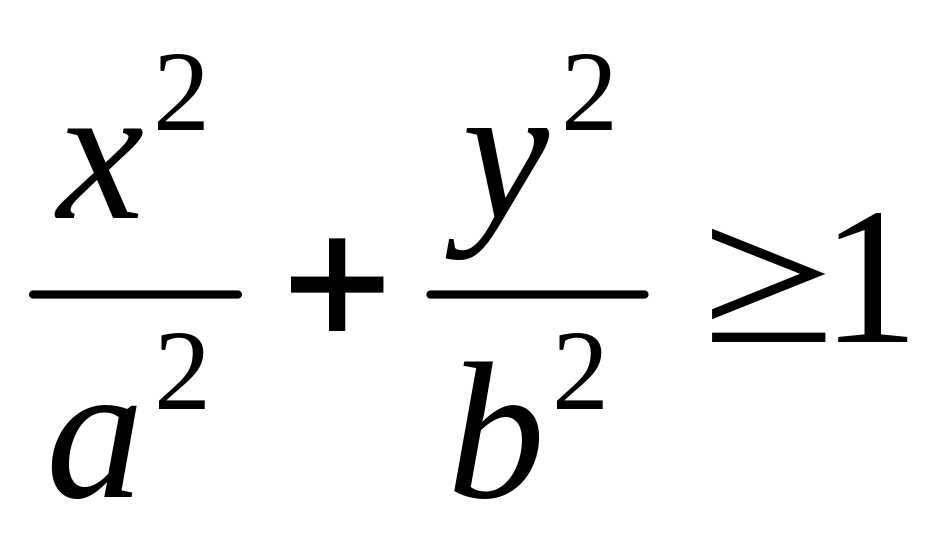• , т.е. гиперболоид лежит вне эллиптического цилиндра, образующие которого параллельны оси (ОZ);

• Однополостный гиперболоид симметричен относительно координатных плоскостей, координатных осей и начала координат.

Исследуем форму этого гиперболоида методом сечений.

I. Пересечём гиперболоид плоскостью, параллельной (ХОУ), её уравнение z = h. Уравнения сечения будут ()

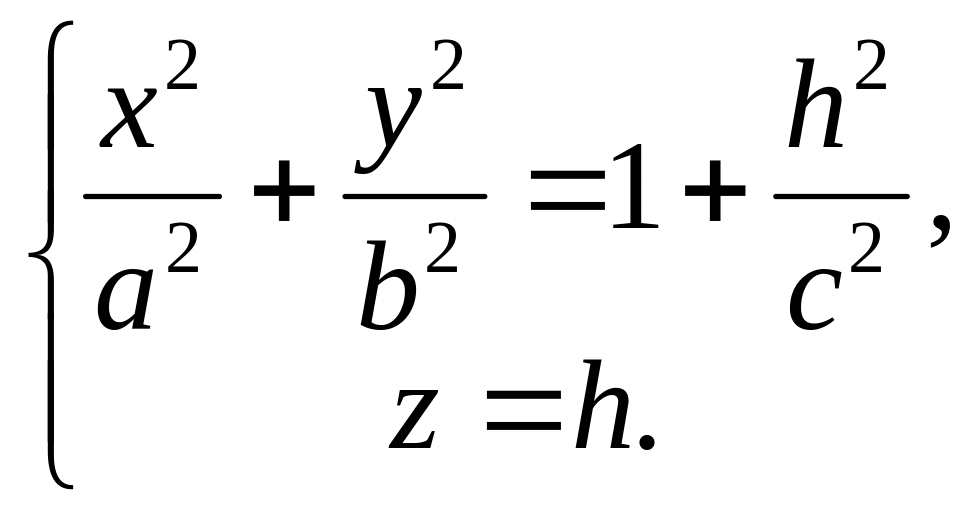При любом h это уравнение определяет эллипс с полуосями а и b . Наименьший эллипс получается при h = 0, т.е. в плоскости (ХОУ). При возрастании h полуоси эллипсов увеличиваются и стремятся к бесконечности (рис. 24). II. При пересечении гиперболоида плоскостями у = m, параллельными плоскости (УОZ). Уравнения сечений у = m. () Возможны случаи: 1) b  m  b. Сечениями будут гиперболы, действительные оси которых параллельны оси (ОХ) и полуоси имеют длину

Рис. 24

а и b . Наибольшие полуоси получаются при m = 0. При увеличении m полуоси уменьшаются и стремятся к нулю. Следовательно, ветви гиперболы сближаются.

2)m = b. В этом случае . Это уравнение определяет пару пересекающихся прямых. Итак, плоскости у = b и у =b пересекают каждая гиперболоид по паре пересекающихся прямых.

3) m  b. В этом случае уравнения () определяют гиперболу, действительная ось которой параллельна оси (ОZ). При увеличении m полуоси будут возрастать, следовательно, ветви гиперболы удаляются друг от друга (рис. 24).

III. При пересечении гиперболоида плоскостями х = n, параллельными плоскости (УОZ) получим результаты, аналогичные результатам предыдущего пункта (проведите это исследование сами).