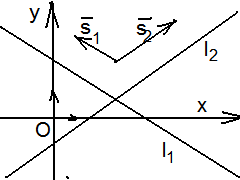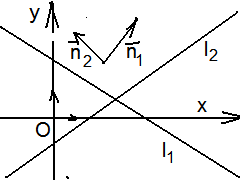- •Аналитическая геометрия
- •Содержание
- •I. Элементы векторной алгебры
- •1.1. Определение и свойства векторов
- •1.2. Сложение векторов
- •1.3. Умножение вектора на действительное число
- •1.4. Коллинеарные векторы
- •1.5. Компланарные векторы
- •1.6. Векторные пространства
- •1.7. Линейная зависимость и независимость векторов
- •1.8. Базис векторного пространства. Координаты вектора
- •1.9. Проекция на прямую параллельно данной плоскости
- •1.10. Проекция вектора на ось
- •1.11. Ортогональная проекция вектора на ось
- •1.12. Скалярное произведение векторов
- •1.13. Метод координат на плоскости и в пространстве
- •1.14. Векторное произведение векторов
- •1.15. Смешанное произведение векторов
- •II. Образы первой ступени
- •2.1. Условия, определяющие фигуру в системе координат
- •2.2. Прямая в аффинной системе координат на плоскости и в пространстве
- •2.2.1. Уравнения прямой, проходящей через данную точку параллельно данному вектору
- •2.2.2. Уравнения прямой, проходящей через две точки
- •2.2.3. Общие уравнения прямой
- •I.Общее уравнение прямой на плоскости
- •II. Общие уравнения прямой в пространстве
- •2.2.4. Исследование взаимного расположения прямых
- •2.3. Прямая в прямоугольной системе координат на плоскости
- •2.3.1. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
- •2.3.3. Нормальное уравнение прямой
- •2.3.4. Угол между двумя прямыми, заданными общими уравнениями
- •2.3.5. Угол между наклонными прямыми, заданными уравнениями с угловыми коэффициентами
- •2.3.6. Расстояние от точки до прямой
- •2.4. Пучок прямых на плоскости
- •2.7. Прямая и плоскость в пространстве
- •2.7.1. Плоскость в аффинной системе координат
- •I.Уравнения плоскости, проходящей через данную точку параллельно двум данным векторам
- •II. Уравнения плоскости, проходящей через три данные неколлинеарные точки
- •III. Общее уравнение плоскости
- •IV. Исследование взаимного расположения двух плоскостей
- •2.7.2. Плоскость и прямая в прямоугольной системе координат
- •I. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- •II. Угол между двумя плоскостями
- •III. Угол между прямой и плоскостью
- •IV. Расстояние от точки до плоскости
- •4.1. Элементарная теория линий второго порядка
- •4.1.2. Эллипс
- •4.1.3. Гипербола
- •4.1.4. Парабола
- •4.1.5. Эллипс, гипербола и парабола в полярных координатах
- •4.2. Упрощение уравнения линии второго порядка
- •4.3. Поверхности
- •4.3.1. Цилиндрические поверхности
- •4.3.2. Конические поверхности
- •4.3.3. Поверхности вращения
- •4.3.4. Эллипсоид
- •4.3.5. Однополостный гиперболоид
- •4.3.6. Двуполостный гиперболоид
- •4.3.7. Гиперболический параболоид
- •4.3.8. Прямолинейные образующие поверхности
2.3.4. Угол между двумя прямыми, заданными общими уравнениями
Дано: R = , l1 : A1x + B1y + C1 = 0, l2 : A2x + B2y + C2 = 0.
Найти один из углов
![]() .
.
Замечание. Очевидно, достаточно найти только один из углов между прямыми.
Решение: 1-ый способ. Из
уравнений l1
и l2
следует, что вектор
|
Рис 23 |
(Вывод формулы (31) можно проводить в
любой аффинной системе координат).
Воспользовавшись тем, что данная система
координат прямоугольная, перепишем
формулу (31) в координатах. Получим
![]() .
Окончательно получим
.
Окончательно получим
![]() (32)
(32)
2-ой способ. Из уравнений l1
и l2
следует, что вектор
|
Рис. 24 |
Переписав полученную формулу в координатах, получим
. (32)
Замечание. Формулу (32) можно использовать только в том случае, когда прямые заданы общими уравнениями в прямоугольной системе координат.
Следствие. Две прямые перпендикулярны тогда и только тогда, когда А1А2 + В1В2 = 0 (33).
Задача. Дано. R
=
,
![]() ,
,
![]() ,
,
![]() ,
l1 : 3х
4у + 11 = 0,
,
l1 : 3х
4у + 11 = 0,
l2 : 5х + у + 8 = 0.
Найти .
Решение. Используем формулу (31). В
нашем случае
![]() =
=![]() ,
,
![]() .
Следовательно,
.
Следовательно,
![]() ;
;
![]() ,
,
![]() .
Подставив в формулу (31), получим
.
Подставив в формулу (31), получим
![]() .
.
2.3.5. Угол между наклонными прямыми, заданными уравнениями с угловыми коэффициентами
Дано: R = , l1 : у = к1 х + в1, l2 : у = к2 х + в2.
Найти ориентированный угол, на который нужно повернуть l1, чтобы она стала параллельной l2.
Решение. Из уравнений l1
и l2
следует, что
Итак,
|
Рис. 25 |
Следствие. Две наклонные прямые перпендикулярны тогда и только тогда, когда
![]() (35)
(35)
Задача. Дано: R = , l1 : 3х + 4у +12 = 0, l2 : 4х 7у 1 = 0.
Найти тангенс угла между прямыми l1 и l2.
Решение. Используем формулу (34).
Для этого нужно найти угловые коэффициенты
данных прямых. Разрешая уравнения прямых
относительно у, получим, что
![]() ,
,
![]() .
Следовательно,
.
Следовательно,
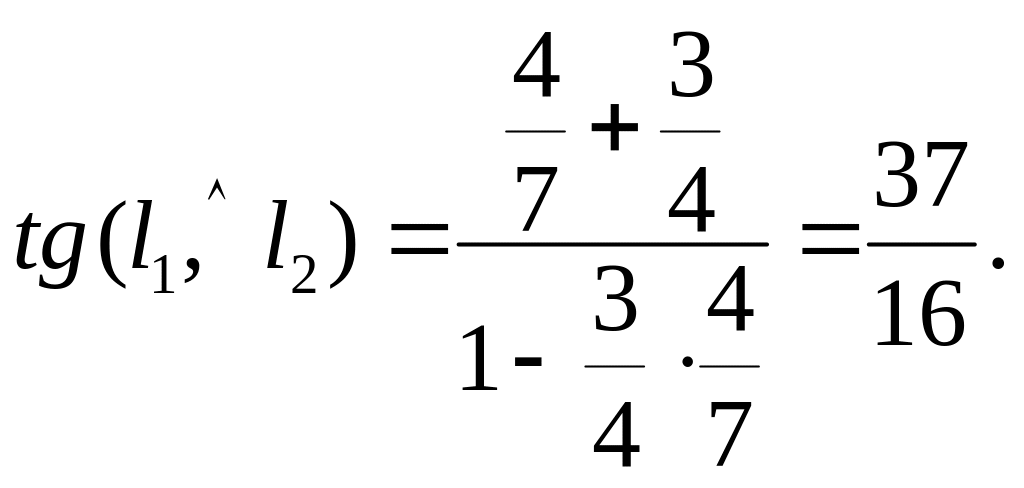
Задача. Дано: R = , l1 : 3х + 4у +12 = 0, l2 : 4х + 3у 24 = 0.
Найти уравнения биссектрис углов, образованных l1 и l2.
Решение. Если l3
и l4 –
биссектрисы данных углов, то каждая из
них проходит через точку А = l1
l2.
Координаты точки А найдём, решая систему
уравнений
![]() Получим А(
Получим А(![]() ).
).
По определению биссектрисы
![]() =
=
![]() и
и
![]() =
=
![]() .
Обозначим через к угловые коэффициенты
l3 и l4
. Используя формулу (34), получим
.
Обозначим через к угловые коэффициенты
l3 и l4
. Используя формулу (34), получим
![]() .
.
Так как
и
![]() ,
то
,
то
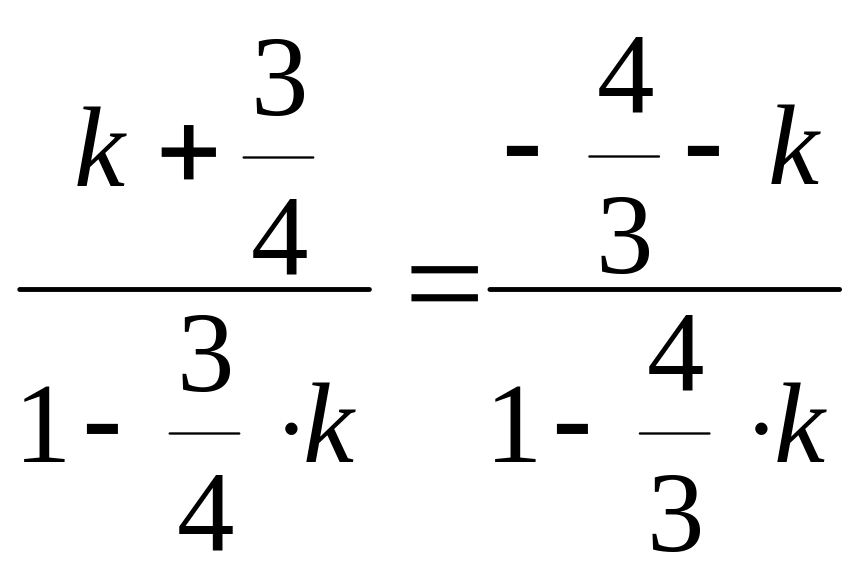 ,
или
,
или
![]() .
Отсюда
.
Отсюда
![]() .
Следовательно,
.
Следовательно,
![]() ,
,
![]() .
Используя уравнение (27), получим
.
Используя уравнение (27), получим
l3 : (у +
![]() )
= 1(х
)
= 1(х
![]() ).
После упрощения l3
: х у
36 =0.
).
После упрощения l3
: х у
36 =0.
Аналогично, l4 : (у + ) = 1(х ). После упрощения l4 : 7х + 7у 12 =0.