Иллюстративные примеры
Рассмотрим применение предлагаемой методики вычисления геометрических характеристик плоских сечений к расчету односвязных и многосвязных поперечных сечений. Учитываем возможность наличия исходных или полученных во время эксплуатации дефектов и повреждений и движение фронтов повреждений, вызванное действием агрессивных сред.
Пример I
Определить геометрические характеристики элементарного неповрежденного поперечного сечения на момент начала его эксплуатации, рис. 4. Координаты точек излома контура сечения приведены в табл. 2.
Таблица 2
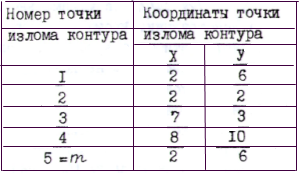
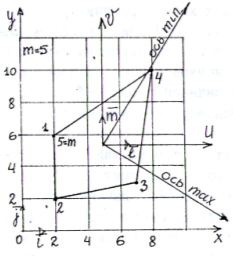
Рис.4
В качестве примера рассматривается четырехугольник т -5, точки излома контура которого занумерованы от 1 до 5 /первая и последняя точки излома контура совпадают/ при обходе контура против движения часовой стрелки, рис.4. Для иллюстрации реализации алгоритма приводим все численные выкладки по данному при меру.
Вычисление величины площади поперечного сечения
С использованием данных
табл. 2
записываем выражения
для радиусов-векторов
точек излома контура и сумм
радиусов-векторов
смежных точек излома контура:
(12)
Вычисляем величины векторных
произведений
:
(13)
Вычисление величины вектора площади поперечного сечения на основе формулы (3) дает результат:
(14)
Отсюда находим величину
площади поперечного сечения
.
Определение положения центра тяжести сечения
Для нахождения величины
вектора статического момента плошали
необходимо предварительно вычислить
величины
и
:
(15)
Из выражения
.
Получаем зависимость между
и
.
Если
,
,
поэтому получаем:
(16)
Вычисляем величину вектора статического момента площади:
(17)
В соответствии с полученной величиной вычисляем радиус-вектор центра тяжести сечения:
(18)
Таким образом, координаты центра тяжести фигуры составляют х0=5.0, у0= 5.4.
Вычисление величин моментов инерции сечения
Для нахождения величин моментов инерции относительно центральных осей вводим систему координат UV с началом в центре тяжести сечения.
Координаты точек излома
контура в новой системе координат UV
'определяются
радиусом-вектором
.
Для нашего конкретного сечения имеем:
(19)
(21)
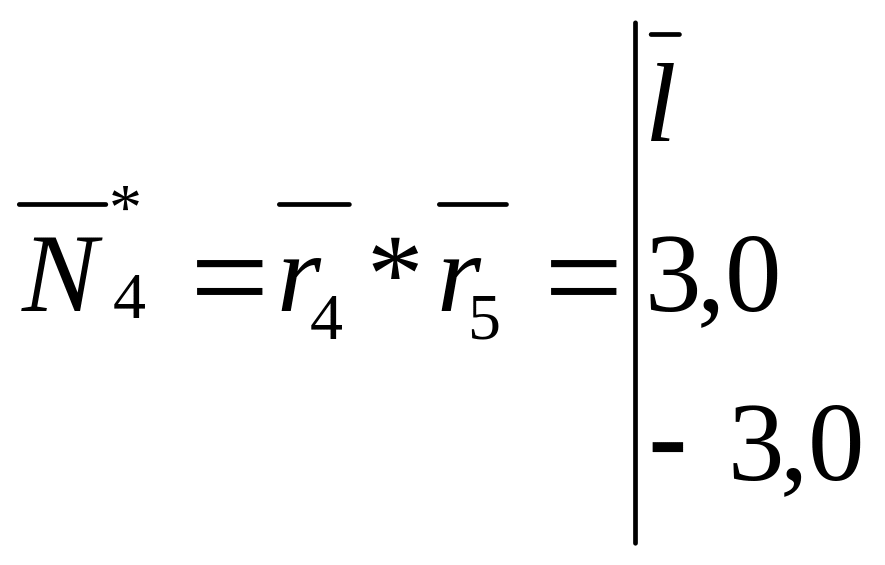
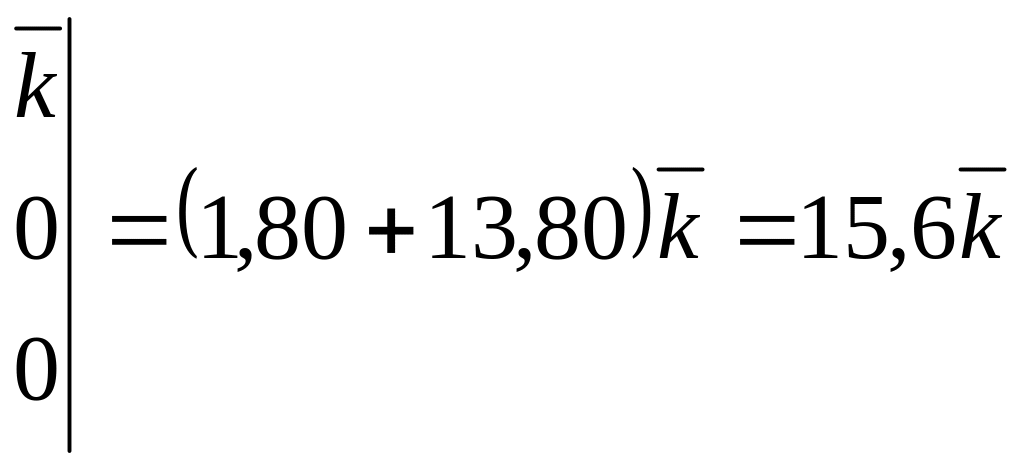
Переходим к вычислению величин Ak, Bk, Ck (7):
(22)
(24)
Все величины, входящие в формулы для моментов инерции JU, JV, JUV, подсчитаны, определяем величины осевых JU и JV и центробежного JUV моментов инерции:
(25)
(26)
(27)
Переходим к определению положения главных осей и нахождению величин главных моментов инерции, принимающих экстремальные значения по отношению к моментам инерции относительно произвольно сориентированных осей.