Цель работы

Объектом исследования является метод Бубнова - Галеркина в применении для расчета прямоугольных пластин.

В процессе выполнения работы:

- изучается методика приведения уравнения и формул к безразмерному виду;

- изучается методика построения аппроксимирующих функций статистическим методом В.3.Власова;

- изучается методика определения амплитуды прогиба методом Бубнова - Галеркина;

- рассматриваются вопросы влияния на напряженное состояние пластин степени вытянутости ее плана;

- рассматриваются особенности применения ЭВМ при решении задач изгиба пластин;

- приобретаются кавыки подготовки исходных данных с использованием ЭВМ "Электроника" ДЗ-28.

Постановка задачи

Рассматриваются такие прямоугольные в плане пластины, нагруженные поперечной нагрузкой q(x,y) произвольного вида - рис.1.

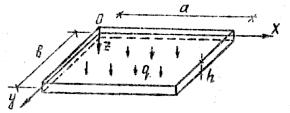
Рис.1

а, б – размеры пластины в плане соответственно по направлению осей x и y; h- толщина пластины.

Условия закрепления пластины на каждой из сторон контура мо­гут быть следующая: жесткое защемление, шарнирное опирание, свободный край. Нагрузка q(x,y) может быть распределена го по­верхности произвольно, но непрерывным образом.

Задание

Для заданной пластины требуется:

1, Построить аппроксимируете функции статическим методом В.З.Власова.

2. Вычислить амплитуду прогиба пластина по методу Бубнова - Галеркика,

3. Построить в заданных сечениях пластины эпюры прогиба W, изгибающих M_x, M_y и крутящего Н моментов, приведенных поперечных сил Q^*_x, Q^*_y с использованием ЭВМ “Электроника” ДЗ-28.

4. Исследовать влияние степени вытянутости плана пластины на ее напряженное состояние.

Технические и языковые средства выполнения работы

При выполнении работы используется микрокалькулятор любого типа, алгоритмический язык Бейсик [5] и ЭВМ “Электроника” ДЗ-28.

Приведение уравнений и формул к безразмерному виду

Для расчета пластин можно использовать уравнения и формулы в размерном виде [1+4]. При этом рассчитывается конкретная пластина с заданными размерами a, b, h,(м), коэффициентом Пуассона μ, модулем упругости Е (Па) – (1 Па = 1 Н/м²), поперечной нагрузкой q (Па).

Однако возможно рассчитать пластину в безразмерном виде, при этом результаты одного конкретного расчета соответствуют многим реальным пластинам.

Для приведения к безразмерному виду уравнений и формул [1+4], описывающих поведение пластины под поперечной нагрузкой, необходимо на основе теории подобия ввести безразмерные переменные и функции по формулам

_{; ; ; ; (1)}

_,

_где - характер изменения нагрузки вдоль оси ,

- характер изменения нагрузки вдоль оси ,

- цилиндрическая жесткость пластины.

При этом внешняя нагрузка представляется в виде

, (2)

поэтому в (1) имеем .

Теперь пластина отнесена к безразмерным координатам , , , - рис.2.

Отношение _{характеризует отношение сторон пластины в плане, являются безразмерной поперечной активной нагрузкой, W(x,y)- безразмерный прогиб.}

_{Также необходимо записать в безразмерном виде уравнение равновесия пластины и напряжения [1+4] для изгибающих Мx(x,y) и My(x,y) и крутящего Н(х,у) моментов и поперечных сил Qx(x,y) и Qy(x,y).}

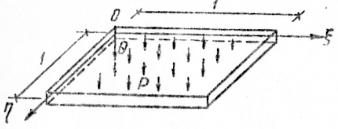
Рис.2

Необходимо помнить, что поперечные силы Q_x, Q_y и моменты M_x, M_y, H в пластинке являются погонными, т.е. приходящимися на единицу длины сечения пластинки и имеющего соответственно размерности Н/м, Нм/м.

Необходимо также обратить внимание на следующее: на контуре пластины поперечную силу Q_x(x,y) ( или Q_y(x,y)) и крутящий момент Н(х,у) можно заменить статически им эквивалентной приведенной поперечной силой Q^*_x(x,y) (или Q^*_у(x,y)).

Подставляя формулы (1) в уравнение Софи Жермен и в выражения М_х, М_у, Н, Q^*_x, Q^*_y [1+4], получим следующие выражения для уравнения равновесия в безразмерном виде и для безразмерных функций:

₍₃₎

_.

_{Предположим, что необходимо рассчитать пластину, определенным образом закрепленную по контуру (например, защемленную), с определенным видом распределения нагрузки (например, равномерным), причем параметры , . Если проводит расчеты в безразмерном виде, приняв , , то получим решение для пластины с произвольными величинами цилиндрической жесткости D, толщины h, размера в плане а, уровня нагрузки q. То есть результаты одного расчета в безразмерном виде соответствуют множеству реальных пластин, поэтому все дальнейшие расчеты проводим в безразмерном виде на основе формул (1) и (3).}