Вычисление амплитуды прогиба пластины По методу Бубнова – Галеркина

Метод Бубнова - Галеркина основан на основе принципа Лагранжа: сумма работ всех внутренних и внешних сил упругой системы на любых малых возможных перемещениях равняется нулю .

За основу берём уравнение равновесия пластины, в безразмерном виде имеющее форму (3). Данное уравнение представляет собой проекцию на ось 6 всех внешних и внутренних сил, действующих на бесконечно малый элемент пластины. Функция прогиба представляет собой представляет собой перемещение в направлении этой же оси. Если подставить выражение для w (5) и (3), получим:

(31)

так как выражение (5) не является решением уравнения (3).

Составляем вариационное уравнение метода Бубнова - Галеркина, выражающее равенство нулю суммы работ всех внешних и внутренних сил пластины на возможных перемещениях

(32)

Подставим (5) в (32) и получаем

(33)

Из (33) находим выражение для амплитуды прогиба

(34)

Для нахождения параметра. В вычисляем определённые двойные интегралы, входящие в формулу (34). Проще всего сделать это следующим образом. Входящие в (34) двойные интегралы представляем в виде произведения одинарных интегралов, например:

(35)

Всего оказывается необходимым вычислить следующие 8 интегралов:

В качестве примера рассмотрим пластину (μ=0.3, γ=1), изображенную на рис.7. Построим для нее статическим методом В.З. Власова аппроксимирующие функции и имеют вид

, (36)

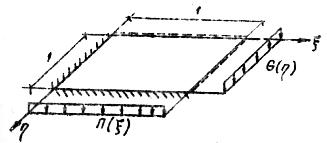
Рис.7

Нагрузка равномерно распределена по пластине, поэтому . Подставляя функции в формулы (35), вычисляем значения определенных интегралов: , , , .

Отметим, что раньше равенства (k=1.2.3.4) получены потому, что пластина симметричная относительно диагонали, проходящей через точки ξ=1, =0-ξ=0, =1. В общем же случае произвольной пластины .

Подставляем вычисленные значения интервалов в формулу (34) и получаем выражение для В

. (37)

Для нашего примера получено В = 0.134 Р₀, теперь выражение для полностью определено.

Построение в заданных сечения пластины эпюр прогиба, изгибающих и крутящих моментов поперечных сил

Для определения в пластине деформации и напряжений необходимо построить эпюры прогиба w, изгибающих М_ξ, М_ и крутящего моментов, поперечных сил - рис.8. Для построения данных эпюр необходимо подставить выражение для (5) в формулы (3), в результате чего получим формулы для приведенных безразмерных моментов и поперечных сил:

Рис.8

(38)

В расчетно-проектировочной работе необходимо построить эпюры, используя сетку координат ξ= 0, 0.25, 0.5, 0.75, 1.0: = 0, 0.25, 0.5, 0.75, 1.0. Таким образом, необходимо найти значения каждой из функций (38) в 25 точках.

Рассмотрим пример построения эпюр для пластины (μ=0.3, γ=1), изображенной на рис.9.

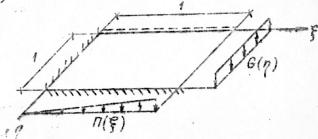
Рис.9

Построенные для нее статическим методом В.З. Власова аппроксимирующие функции имеют вид:

, .

Производные от функции и имеют вид:

; ; ;

; ; ; ;

.

Значения функции и ее производных для пяти значений , а также величины I₁, I₂, I₃, I₄, указаны в таблице 1.

Таблица 1

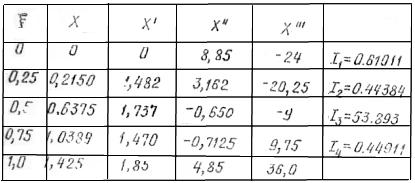
Значения функции и ее производных для пяти значений , а также значений указаны в табл.2.

Таблица 2

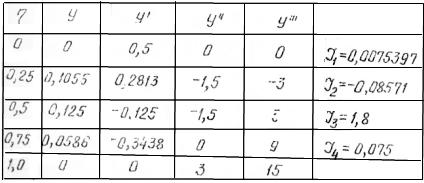
В процессе решения задачи методом Бубнова – Галеркина находим по формуле (37) амплитуду прогиба :

.

Для дальнейшего решения задачи принимаем Р₀=10 и имеем поэтому В=0.237.

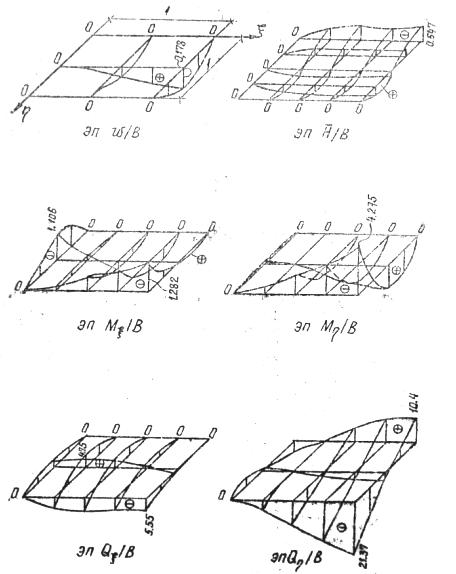
Далее по формуле (38) вычисляем значения функции w, , М_ξ, М_, для нашей сетки координат и по полученным значениям строим эпюры этих функций. На рис.10 приведены данные эпюры для В=1, т.е. эпюры w/B, , М_ξ/В, М_/В, .

Следует помнить, что на эпюрах положительные значения принято откладывать вверх, а положительные значения , М_ξ, М_ - вниз.

Также следует помнить, что при выполнении расчетно-проектировочной работы требуется построить каждую из эпюр по 25 вычисленным значениям. Эпюры необходимо строить в большом масштабе.

Все значения, необходимые для построении эпюр, вычисляются с помощь. ЭВМ “Электроника” Д3-28 по прилагаемой ниже программе.

На основе полученных эпюр возможно определить значения нормальных , и касательного напряжений в конкретных точках любого слоя пластины. Наибольшие значения нормальных напряжений будут из нижней (знак «+» в формуле (39)) и на верхней (знак «-» в формуле (39)) поверхностях пластины

, , (39)

Отметим, что переход от безразмерных к размерным функциям осуществляется на основе формул (3), например, для моментов имеет , .

При использовании энергетической теории прочности условие прочности рассматриваемых упругих пластин запишем в виде:

. (40)

где [σ]- нормативное напряжение для материала пластины.