Исследование характера изменения бимоментных напряжений вдоль стержня и их вклада в суммарные напряжения
Таблица 2
После подсчета величин напряжений
в точке 7 для различных сечений стержня
возможно определить вклад бимоментных
напряжений в суммарные. Подсчет производим
по формуле
и заносим результаты в табл. 2.
Затем выбираем на эпюре
одну из точек с максимальной ординатой,
например, точку 8. Проделываем те же
действия, что и в первом случае, и заносим
результаты в следующие четыре строки
табл.2.
Выбираем на эпюре
точку с максимальной ординатой (точка
5). Используя значения
из табл.1, подсчитываем значения
,
,
,
в точке 5 для различных сечений стержня.
Выбираем на эпюре точку с максимальной ординатой (точка 4). Проделываем те же действия, что и в предыдущем случае, и заносим результаты в табл.2.
По данным табл.2 строим эпюры изменения указанных величин вдоль оси OZ- рис. 19, 20, 21, 22.
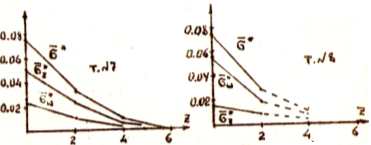
Рис.19 Рис.20
Рис.21 Рис.22
Анализ данных эпюр углов закручивания
,
депланации
М-1, бимомента
,
изгибо-крутящего момента
,
а также
проводится с помощью нижеприведенной
программы. Программа работает при
заданных значениях начальных параметров
(их определение дается в соответствующем
разделе настоящих методических указаний),
при внешней нагрузке, состоящей из одной
из сосредоточенной силы
,
приложенной сечении с координатой
,
и одной распределенной нагрузки
,
действующей на участке, начиная с сечения
до сечения
.
Для работы программы необходимо подготовить и ввести следующие исходные данные:
- шифр студента, любое целое четырехзначное
число,
-
характерный размер поперечного сечения
(М),
-
толщину профиля (М),- множитель в выражении для координаты
центра изгиба
,
в множителе
учитывается знак координаты
.
-
значение сосредоточенной силы (МН),
-
расстояние от левого конца стержня до
точки приложения силы
в метрах (см. рис. 4, 6),
-
значение интенсивности распределенной
нагрузки
,
,
-
соответственно начало и конец участка
приложения распределенной нагрузки
(М),
-
длину стержня (М),
-
число, которое используется при
вычислении шага
вычислений по длине стержня:
.- коэффициент выражения
,
-
коэффициент выражения
,
-
отношение модуля Юнга
к модулю сдвига
,
-
начальный параметр,
-
начальный параметр (М-1),
-
начальный параметр (МН*М2),
-
начальный параметр (МН*М).
Ввод этих величин осуществляется операторами 10-220. Печать исходных данных реализуется операторами 280-430.
В программе дополнительно используются
следующие обозначения:
где
,
,
-
сосредоточенный крутящий момент,
-
распределенный крутящий момент с учетом
принятого правила знаков.
При печати результатов используются обозначения:
- координата сечения (М) стержня, в контрольном примере, и сравнить полученные результаты с данными, приводимыми в контрольном примере.
ПРИМЕР
10 OPEN “LP1”
20 REM РАСЧЕТ ТОНКОСТЕННОГО СТЕРЖНЯ
30 PRINT “ИСХОДНЫЕ ДАННЫЕ”
40 INPUT “ШИФР СТУДЕНТА”
50 INPUT “A=”; A
60 INPUT “BET=”; BET
70 INPUT “E=”; E
80 INPUT “PP=”; P
90 INPUT “A1=”; A1
100 INPUT “Q=”; Q
110 INPUT “B=”; B
120 INPUT “C=”; C
130 INPUT “L=”; L
140 INPUT “L1=”; L1
150 INPUT “D=”; D
160 INPUT “OMEGA=”; OMEGA
170 INPUT “EE=”; EE
180 INPUT “EO=”; EO
190 INPUT “QO=”; QO
200 INPUT “Q10=”; Q10
210 INPUT “BO=”; BO
220 INPUT “HO=”; HO
230 DZ=L/L1
240 K=SQR (D/ (EO*OMEGA) )*BET/(A^2)
250 B=4.8*A*BET^3*E/E
260 MM=-PP*E*A
270 M=-Q*E*A
280 PRINT #”РАСЧЕТ ТОНКОСТЕННОГО СТЕРЖНЯ”
290 PRINT #
300 PRINT #”ШИФР СТУДЕНТА”; NZ
310 PRINT #
320 PRINT #”A=”; A, “BET=”, BET, “E=”, E
330 PRINT #
340 PRINT #”PP=”, PP, “A1=”, A1
350 PRINT #
360 PRINT #”Q=”; Q, “B=”; B; “C=”; C
370 PRINT #
380 PRINT #”L=”; L; “L1=”;, L1; “D=”; D; “OMEGA=”; OMEGA;
390 PRINT #”EE=”; EE; “EO=”; EO
400 PRINT #
410 PRINT #”QO=”, QO; “Q10=”; Q10; “BO=”; BO; “HO=”; HO
420 PRINT #
430 PRINT #”K=”; K; “θ=”; θ; “MM=”; MM; “M=”; M
440 PRINT #
450 DEF FNS(X)=(EXP(X)-EXP(-X))/2
460 DEF FNS(X)=(EXP(X)+EXP(-X))/2
470 FOR Z=0 TO L STEP DZ
480 KZ=K+Z
490 T=QO+FNS(KZ)/K*Q10+(1-FNC(KZ))/6*90+(Z-FNS(KZ)/K)/6*110
500 T1=FNC(KZ)*Q10-K*FNS(KZ)/6*70+(1-FNC(KZ))/6*110
510 BB=-G*FNS(KZ)/K*Q10+K+FNS(KZ)*80+FNS(KZ)/K*110
520 MOMEGA=MOMEGA-MM*FNC(KZ)
560 IF Z<=A1 GOTO 710
540 KZ=K*(Z-A1)
550 T=T-MM*((Z-A1)-FNS(KZ)/K)/6
560 T1=T1-MM*(1-FNC(KZ)/K)/6
570 BB=BB-MM*FNS(KZ)/K
580 MOMEGA=MOMEGA-MM*FNC(KZ)
590 IF Z<=B GOTO 710
600 KZ=K*(Z-B)
610 T=T-M/6*((Z-B)^2/2+1/K^2*(1-FNC(KZ)))
620 T1=T1-M/6*(Z-B-FNS(KZ)/K)
630 BB=BB-M/K^2*(FNC(KZ)-1)
640 MOMEGA=MOMEGA-MM*FNS(KZ)/K)
650 IF Z<=C GOTO 710
660 KZ=K*(Z-C)
670 T=T+M/G*((2-C)^2/2+1/K^2*(1-FNC(LZ)))
680 T1=T1+M/6*(Z-C-FNS(KZ)/K)
690 DD=DD*M/K^2*(FNC(KZ)-1)
700 MOMEGA=MOMEGA+M/K/FNS(KZ)
710 REM КОНЕЦ ЦИКЛА
720 REM
730 BB=BB/A^2
740 MOMEGA=MOMEGA/A
750 MO=G*T1/A
760 PRINT 0 “Z=”; Z
770 PRINT 0 “T=”; T; “T1=”; T1; “BB=”; BB
780 PRINT 0 “MOMEGA=”; MOMEGA; “MO=”; MO
790 PRINT 0
800 NEXT Z
810 CLOSE
820 STOP
СХЕМА АЛГОРИТМА
