Построение эрюр угла закручивания , депланации , бимомента и изгибающего-крутяшего момента

После нахождения величин всех начальных параметров с ис­пользованием выражений (5) можно построить эпюры функций , , , по длине балки. В качестве примера рассмотрим балку, изображенную на рис. 4, 7. Вид эпюр приведен на рис. 9. Вместо эпюр и приведены эпюры и , ординаты которых используются при построении эпюр и . Контролем правильности построения эпюр служит выполнение граничных условий при , . В данном случае при должно получиться , , а при - , . Контролем также может служить и вид эпюры , которая должна иметь постоянные ординаты на участках, где . Полезно также учитывать, что пропорционален , а .

В конце методических указаний производится программа расчета, составленная на алгоритмическом языке “Бейсик” УКМЦ Электроника МС-0511. Приводится схема алгоритма и инструкция к программе, позволяющая вычислять ординаты эпюр , , , .

Рис.9

Построение эпюр нормальных , и касательных , напряжений для ряда сечений стержня

Для стержня с поперечным сечением, изображенным на рис.3 методических указаний [5], с закреплениями концов и нагрузкой, изображенной на рис. 4, 7 данных методических указаний, были получены следующие значения величин:

, -с. 13, 22 [5],

, , , - соответственно выражения (17), (15) и рис.23, 25, 20, 21 методических указаний [5], , , , - рис. 4, 9 данных методических указаний. Эпюры приведены соответственно на рис. 10, 12, 14, 16. Значения в различных сечениях стержня приведены в табл.1.

Таблица 1

Рис.10 Рис.11

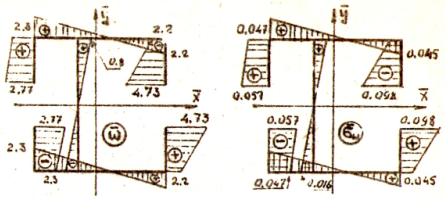
Рис.12 Рис.13

Преобразуем выражения (2), (3) для нормальных и касательных напряжений следующим образом:

(19)

.

На рис. 11, 13 приведены эпюры , , которые получаются из эпюр и делением каждой ординаты соответственно на и . На рис. 15, 17 приведены эпюры , . Ординат этих эпюр получаются делением ординат и соответственно на и .

Одной из задач, которая преследуется при построении эпюр и , является определение положительных направлений касательных напряжений с помощью знаков эпюр и и направлений обхода контура. Положительные направления касательных напряжений на рис. 15, 17 показаны стрелками. При этом надо учитывать, что при истинное направление касательных напряжений , совпадает с приведенным на рис. 15, 17, а если , то касательные напряжения соответственно противоположно.

Рис.14 Рис.15

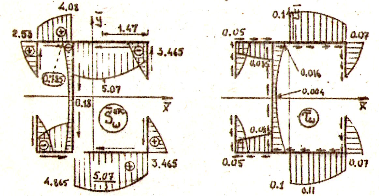
Рис.16 Рис.17

Рис.18

Поясним порядок выбора направления действия касательных напряжений. Рассмотрим сечения стержня при взгляде на них по направлению оси OZ. Методика выбора направления действия напряжений будет следующей. В рассматриваемом сечении че­рез точку, для которой определяется положительное направление касательного напряжения, перпендикулярно контуру проездам про­дольную плоскость. Ту часть сечения, на которую указывает на­правление обхода контура в данной точке, при построении эпюры отбрасываем. Тогда при положительном знаке эпюры в этой точке в продольной плоскости касательные напряжения совпадают с направлением оси 0Z. При отрицательном знаке на эпюре касательные напряжения совпадают с направлением оси OZ. Направления касательного касательного напряжения в поперечном сечении определяется по закону парности касательных. Напряжений.

Для определения направления касательного напряжения применяется эта же методика, но только положительным направлением на продольном сечении считается то, которое противопо­ложно оси Z. Соответственно для поперечных сечении стержня при взгляде на них против направления оси OZ касательные на­пряжения имеют противоположное направление. На рис. 15, 17 произведены направления касательных напряжений на поперечных сечениях при взгляде на них по направлению оси OZ.

Пронумеруем характерные точки контура поперечного сечения, в которых эпюры претерпевают изменения рис. 18.

Выберем на эпюре одну из точек с максимальной ординатой, например, точку 2. Используя значения и из табл.1, подсчитаем значения , , в точке 2. При этом в зависимости от координаты поперечного сечения величина напряжений будет меняться. Установим, по каким законам меняются вдоль оси компоненты напряжений.