12.3. Обчислення визначників n-го порядку за означенням.

Для того, щоб обчислювати визначник за означенням, треба вміти формувати (або генерувати) множину всіх перестановок чисел .

Спосіб генерування всіх перестановок чисел 1, 2, …..., n.

n=2	n=3
1,2 2,1	поч.	сер.	кін
	3, 1, 2	1, 3, 2	1, 2, 3
	3, 2, 1	2, 3, 1	2, 1, 3

При такому способі виписування перестановок можна одразу визначити парність перестановок, а отже одразу визначити знак, з яким відповідний добуток увійде у відповідну алгебраїчну суму (визначник):

+ 1, 2, 3	+ 2, 3, 1
- 2, 1, 3	+ 3, 1, 2
- 1, 3, 2	- 3, 2, 1

Перестановки чисел 1, 2, 3, 4

+ 1, 2, 3, 4	- 1, 2, 4, 3	+ 1, 4, 2, 3	- 4, 1, 2, 3
- 2, 1, 3, 4	+ 2, 1, 4, 3	- 2, 4, 1, 3	+ 4, 2, 1, 3
- 1, 3, 2, 4	+ 1, 3, 4, 2	- 1, 4, 3, 2	+ 4, 1, 3, 2
+ 2, 3, 1, 4	- 2, 3, 4, 1	+ 2, 4, 3, 1	- 4, 2, 3, 1
+ 3, 1, 2, 4	- 3, 1, 4, 2	+ 3, 4, 1, 2	- 4, 3, 1, 2
- 3, 2, 1, 4	+ 3, 2, 4, 1	- 3, 4, 2, 1	+ 4, 3, 2, 1

Вказаний спосіб очевидним чином розповсюджується на загальний випадок чисел . Основна ідея: зведення задачі побудови перестановок чисел до задачі побудови перестановок чисел .

Формула для обчислення визначника 4-го порядку

Дописати формулу до кінця самостійно (всього в ній буде 24 доданки-добутки).

Кількість числа перестановок чисел 1, 2, 3, 4, n.

Позначимо — кількість перестановок чисел . З попереднього розгляду маємо: . Із способу формування всіх перестановок чисел випливає формула:

В цій формулі можна замість підставити :

Використовуючи метод математичної індукції, можна легко довести:

(читається “н-факторіал”)

Значить, наприклад, при обчисленні визначника 5-го порядку за означенням виникне сума, у якій буде доданків, а при обчисленні визначника 6-го порядку відповідна сума буде мати доданків.

Як бачимо, при обчисленні визначників за означенням доводиться мати справу з досить громіздкими сумами з великою кількістю доданків. Але в деяких випадках можна при обчисленні визначника за означенням зменшити кількість доданків, відкинувши нульові доданки.

Приклад.

1,4 2,1 3,2 4,3 5,5

4 1 2 3 5

3 + 0 + 0 + 0 +0=3

=

12.4. Метод Гауса обчислення визначників.

Для обчислення визначників матриць з довільними числовими елементами використовується інший спосіб - метод Гауса.

Метод Гауса є найбільш економічним і ефективним методом обчислення визначників з числовими елементами. Цей метод базується на таких трьох властивостях визначників:

1) Визначник трикутної матриці (відносно головної діагоналі) дорівнює добуткові елементів головної діагоналі:

(довести самостійно за допомогою означення визначника).

2) Спільний множник елементів деякого рядка можна винести за знак визначника:

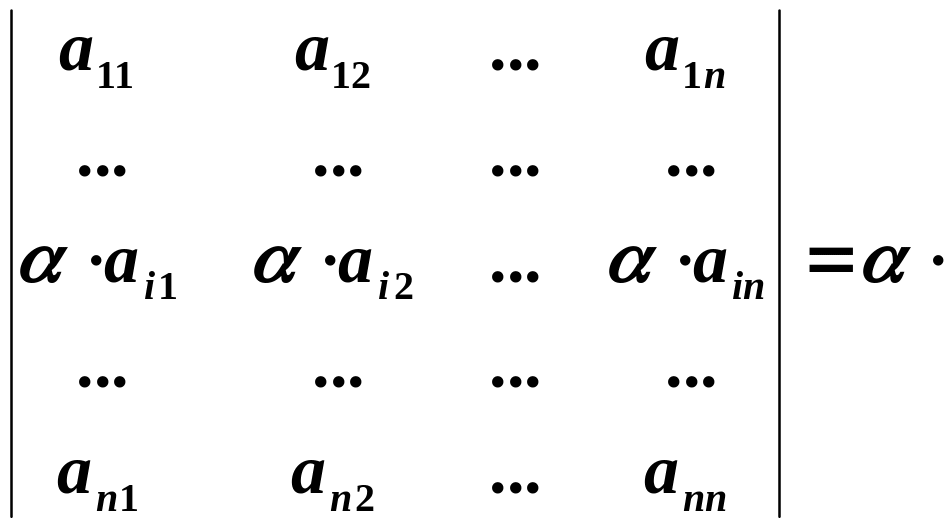
(те саме вірне для стовпчиків).

(довести самостійно за допомогою означення визначника).

3) При виконанні гаусівських перетворень виключення над матрицею визначник не змінюється; ця властивість випливає з більш загальної: якщо до деякого рядка додати інший рядок, помножений на деяке (довільне) число, то визначник не зміниться:

(довести самостійно за допомогою означення визначника).

Приклад: