
- •Розділ II.
- •§8. Системи лінійних рівнянь і n-вимірні вектори.
- •8.1. Поняття системи лінійних рівнянь, системи лінійних нерівностей та їх розв’язків.
- •8.2. Поняття n-вимірного вектора і n-вимірного лінійного векторного простору.
- •8.3. Загальні теореми про множину розв’язків систем лінійних рівнянь.
- •8.4. Теорема Крамера для квадратних слр.
- •§9. Лінійні векторні простори.
- •9.1. Загальне поняття лінійного векторного простору.
- •9.2. Підпростори лінійних векторних просторів.
- •9.3. Геометрія лінійних векторних просторів.
- •9.4. Опуклі множини в п-вимірному просторі.
- •§10. Метод Гауса розв’язання систем лінійних рівнянь.
- •10.1. Загальна ідея методу Гауса.
- •10.2. Поняття загального розв’язку слр.
- •10.3. Елементарні перетворення слр .
- •Позначення: ;
- •Позначення: .
- •10.4. Перетворення виключення.
- •10.5. Умова несумісності слр.
- •10.6. Вилучення залежних рівнянь.
- •10.7. Алгоритм методу Гауса.
- •10.8. Матрична форма методу Гауса.
- •§11. Елементи матричної алгебри.
- •11.1. Вступ до матричної алгебри.
- •11.2. Арифметичні операції над матрицями.
- •11.3. Економічне тлумачення операції матричного множення.
- •11.4. Властивості операцій над матрицями.
- •11.5. Мультиплікативна форма методу Гауса
- •11.6.Обернена матриця, її обчислення і застосування.
- •11.7. Застосування оберненої матриці до розв’язання систем лінійних рівнянь.
- •§12. Визначники n-го порядку, їх обчислення та застосування.
- •12.1. Аналіз спільних властивостей визначників 2-го та 3-го порядку.
- •12.2. Поняття визначника n-го порядку.
- •12.3. Обчислення визначників n-го порядку за означенням.
- •Спосіб генерування всіх перестановок чисел 1, 2, …..., n.
- •Перестановки чисел 1, 2, 3, 4
- •Формула для обчислення визначника 4-го порядку
- •12.4. Метод Гауса обчислення визначників.
- •12.5. Розкладення визначника за елементами рядка (або стовпчика).
- •12.6. Детермінантна формула для оберненої матриці.
- •12.7. Властивості визначників.
- •12.8. Теорема Крамера (загальний випадок).
- •12.9. Інтерполяційний многочлен.
- •§13. Лінійна залежність і незалежність n-вимірних векторів.
- •13.1. На підходах до поняття лінійної залежності і незалежності.
- •13.2. Загальне поняття лінійної залежності і незалежності.
- •13.3. Лінійна залежність в ℝ2 і ℝ3.
- •13.4. Властивості лінійно залежних і лінійно незалежних систем n-вимірних векторів.
- •13.5. Базиси n-вимірних векторних просторів.
- •13.6. Фундаментальна система розв’язків системи лінійних рівнянь.
- •Якщо скористатися результатом роботи методу Гаусса
- •13.7. Критерій сумісності систем лінійних рівнянь.
11.7. Застосування оберненої матриці до розв’язання систем лінійних рівнянь.
Припустимо, що ми маємо СЛР
,
де матриця
є квадратною. Припустимо, що
має обернену матрицю
.
Помножимо на
![]() обидві частини векторно-матричного
рівняння:
обидві частини векторно-матричного
рівняння:
![]() .
.
Користуючись властивостями матричного множення (якими ?), отримаємо:
![]() .
.
Але
![]() .
Отже отримуємо формулу
розв’язку СЛР з використанням оберненої
матриці:
.
Отже отримуємо формулу
розв’язку СЛР з використанням оберненої
матриці:
![]() .
.
Ця формула найбільш
корисна, коли при фіксованій матриці
вектор вільних членів
![]() може варіюватися. Наприклад, у наведеному
вище прикладі, пов’язаному з математичною
економікою, можна досліджувати різні
варіанти плану виробництва. Тоді можна
один раз обчислити обернену матрицю
і швидко знаходити відповідні планові
показники, не розв’язуючи кожного разу
СЛР, а обчислюючи лише добуток матриці
на вектор.
може варіюватися. Наприклад, у наведеному
вище прикладі, пов’язаному з математичною
економікою, можна досліджувати різні
варіанти плану виробництва. Тоді можна
один раз обчислити обернену матрицю
і швидко знаходити відповідні планові
показники, не розв’язуючи кожного разу
СЛР, а обчислюючи лише добуток матриці
на вектор.
Метод оберненої матриці застосовний не лише у випадку квадратних СЛР.
Приклад. Розглянемо СЛР:
![]()
Утворимо матрицю з коефіцієнтів при змінних і , тобто, фактично, з 2-го і 4-го стовпчиків основної матриці СЛР:
 – розширена
матриця СЛР,
– розширена
матриця СЛР,
![]() – основна матриця
СЛР,
– основна матриця
СЛР,
![]() – матриця, утворена
з 2-го і 4-го стовпчиків
– матриця, утворена
з 2-го і 4-го стовпчиків
основної матриці .
Знайдемо
![]()
![]()
![]() =
=![]() .
.
Перевірка:![]()
![]() =
=
![]() =
=![]() =
=![]() .
.
Обернена матриця обчислена вірно.
Помножимо
![]() зліва на розширену матрицю СЛР:
зліва на розширену матрицю СЛР:
![]() =
=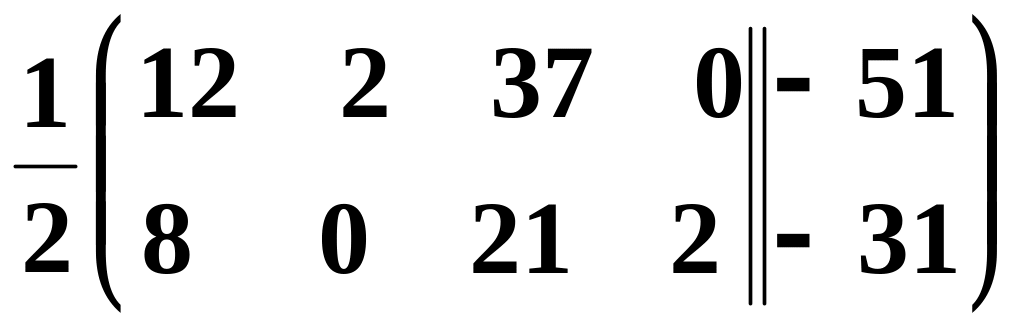 =
=
=
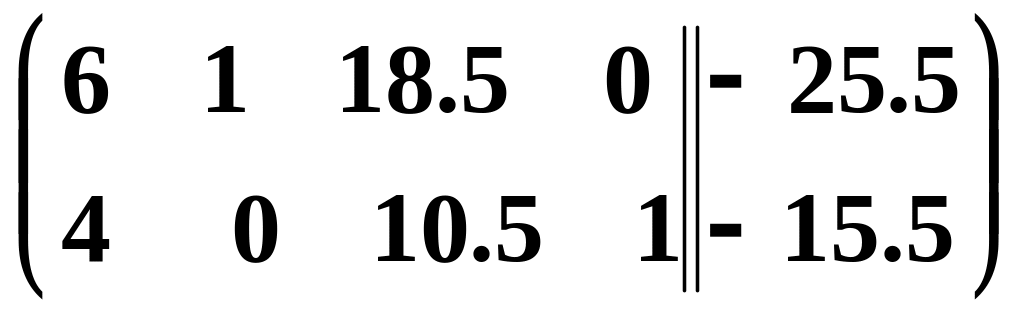 – розширена матриця СЛР, розв’язаної
відносно змінних
і
,
що дозволяє виписати загальний розв’язок
СЛР:
– розширена матриця СЛР, розв’язаної
відносно змінних
і
,
що дозволяє виписати загальний розв’язок
СЛР:
![]() .
.
Вправа. Використовуючи матричну форму запису СЛР, обгрунтувати застосований спосіб розв’язання СЛР.
§12. Визначники n-го порядку, їх обчислення та застосування.
Теорема Крамера для СЛР 2х2 і 3х3 як джерело виникнення поняття визначника. Аналіз понять визначника 2-го і 3-го порядків. Формування поняття визначника n-го порядку як узагальнення понять визначника 2-го і 3-го порядків: формування доданків-множників за допомогою поняття перестановки, визначення знаку доданку-множника за допомогою поняття інверсії. Означення визначника n-го порядку. Загальне формулювання теореми Крамера. Обчислення визначників за означенням за допомогою ітераційного способу генерування всіх перестановок n чисел. Обчислення визначників шляхом формування множини “суттєвих” (ненульових) доданків-добутків. Властивості визначників n-го порядку. Загальний метод обчислення визначників довільного порядку зведенням до трикутного виду за допомогою методу Гаусса. Розкладення визначника за елементами рядка або стовпчика. Детермінантна формула для обчислення оберненої матриці.
Поняття визначника 2-го і 3-го порядків з’явилось в нашому курсі при аналітичному розв’язанні геометричної задачі знаходження перетину прямих ліній і площин (див. § 2). Це поняття використовує теорема і правило Крамера, яке дає формули для обчислення координат точок перетину. Саме так поняття визначника виникло історично. Одразу ж після розгляду зазначеної задачі ми побачили, як поняття визначника дозволяє елегантно і красиво дати формули координатного подання векторного і змішаного добутку(див. §,§ 5,6). Історично поняття визначника виникло при розв’язанні та аналізі систем лінійних рівнянь (СЛР). Якщо метод Гаусса – це алгоритмічний процес, то правило Крамера складається з компактних формул, основними компонентами яких є визначники.
