1.5. Линейные операции над матрицами

Равенство матриц. Две матрицы и равны, если они имеют одинаковые размеры, и элементы матриц, стоящие на соответствующих местах равны между собой: , для всех i,j. То есть равенство матриц означает их тождественное совпадение.

Умножение матрицы на число. Умножить матрицу на число k, значит умножить на это число каждый элемент матрицы: , для всех i,j..

Сложение матриц. Для того чтобы сложить две матрицы одинаковых размеров надо сложить элементы этих матриц, стоящие на соответствующих местах: , для всех i,j.

Пример. Найти матрицу , если , .

C = 4A-2B =4 -2 =

1.6. Умножение матриц

Произведение АВ двух матриц А и В определено тогда и только тогда, когда количество столбцов матрицы А равно количеству строк матрицы В Причем, если - матрица порядка m на n, а -матрица порядка n на k, то произведение АВ=С представляет собой матрицу порядка m на k.. Причем, элементы матрицы С, лежащие на пересечении i-ой строки и j-ого столбца, определяются в соответствие с формулой

, где , .

.

Эта несложная формула и выражает правило произведения матрицы на матрицу , которое часто называют правилом произведения - «строка на столбец». Для того чтобы получить - ый элемент матрицы произведения , надо элементы i-той строки матрицы умножить на соответствующие элементы (совпадает номер столбца и номер строки ) j-ого столбца матрицы и полученные произведения сложить. Эту же процедуру проделать для нахождения каждого из элементов матрицы .

Замечание. Из определения видно, что в общем случае . Матрицы и для которых называются перестановочными.

Пример 1. Найти произведения и , если они существуют, для матриц А= и В= .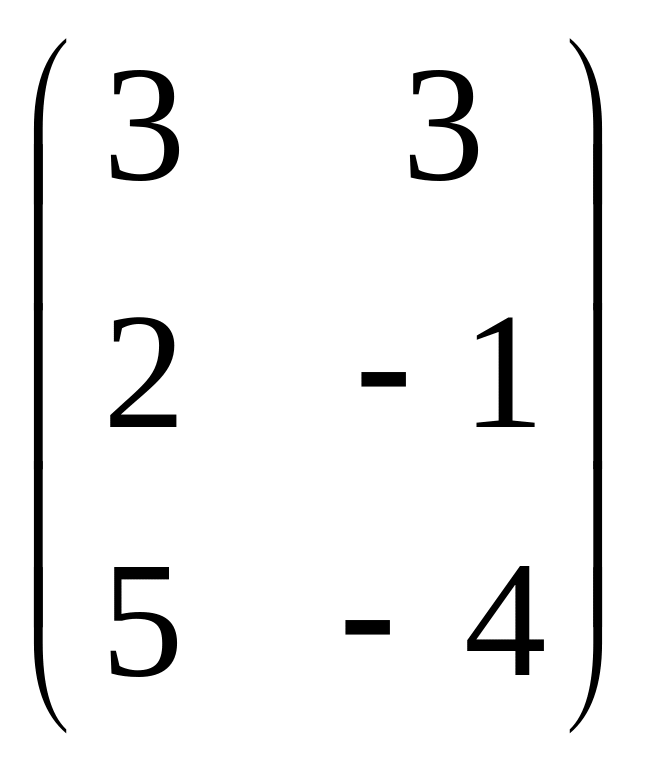

Решение.

.

Например, ,

т.е. вторая строка первой матрицы умножается на второй столбец второй матрицы по указанному выше правилу.

Аналогично находим:

.

Видно, что , т.е. , матрицы А и В не перестановочны.

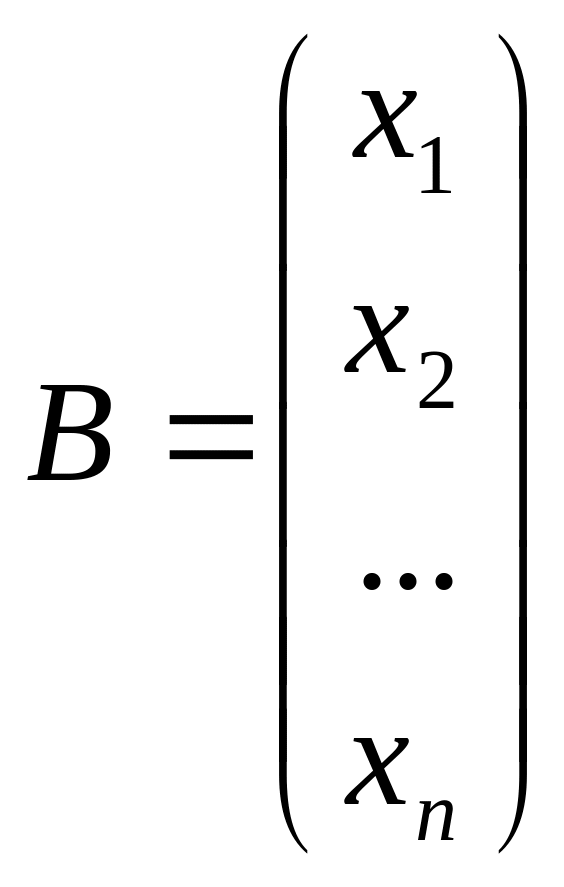Пример 2. Произведение матрицы- строки , на матрицу-столбец дает число:

.

1.7. Обратные матрицы

Операция «деление» в матричной алгебре отсутствует, но для невырожденных матриц т.е. квадратных матриц определитель которых не равен нулю, естественным образом можно ввести понятие обратной матрицы, которая обозначается - (это не , а цельное обозначение обратной матрицы).

Определение. Матрица называется обратной к квадратной матрице , если - единичная матрица.

Можно показать, это для любой невырожденной матрицы существует единственная обратная матрица, которая находится по формуле

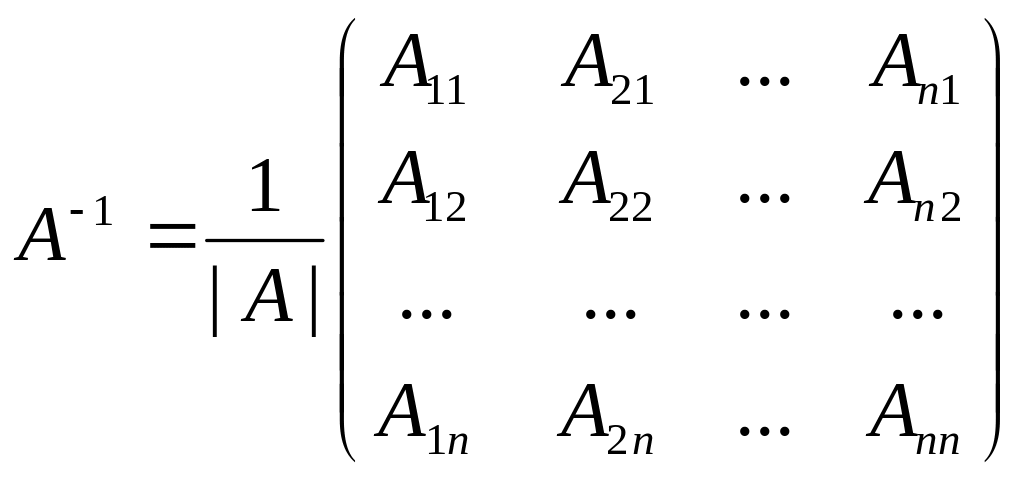, где А_ij - алгебраическое дополнение к элементу а_ij исходной матрицы А. По определению – это определитель, полученный из исходного, вычеркиванием i-ой строки и j-ого столбца, умноженный на (-1)^i+j.

Пример. Найти матрицу Х из уравнения , где , .

Решение. Прежде всего выясним, является ли матрица А невырожденной. Найдем определитель матрицы |A|= . Значит, матрица А – невырожденная и для нее существует обратная А^-1. Умножим обе части равенства Х^.А = В справа (!!!) на А^-1, получим . Учитывая, что - единичная матрица, а умножение на единичную матрицу не изменяет матрицу Х, получим решение уравнения в матричном виде: .

Для того чтобы найти матрицу А^-1 , ищем алгебраические дополнения к каждому из элементов матрицы А:

, тогда .

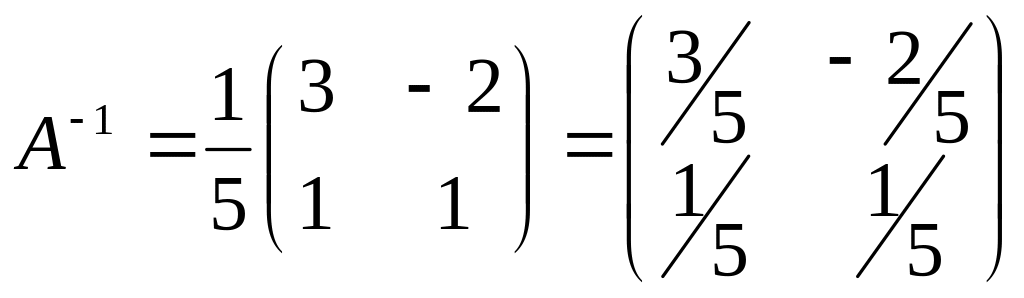Х= .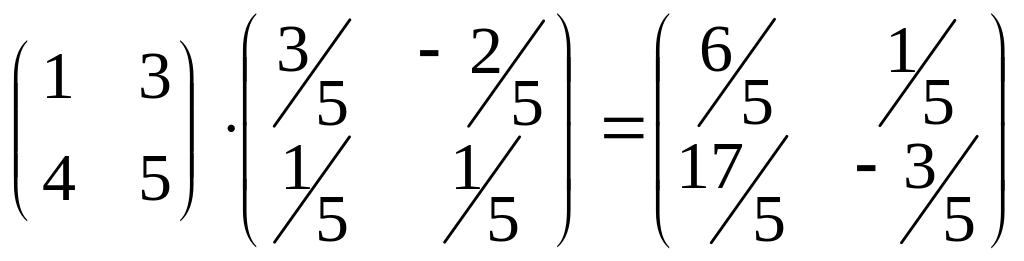

Проверьте результат вычисления прямой подстановкой в исходное уравнение!