
- •Высшая математика
- •Часть 1
- •Предисловие
- •1.Элементы линейной алгебры.
- •1.1.Матрицы и определители 2-го порядка
- •1.2 Матрицы
- •1.3. Определители третьего и более высоких порядков
- •1.4. Свойства определителей
- •1.5. Линейные операции над матрицами
- •1.6. Умножение матриц
- •1.7. Обратные матрицы
- •1.8. Ранг матрицы
- •2. Системы линейных алгебраических уравнений - слау
- •2.1 Основные определения
- •2.2. Матричный метод решения невырожденных систем
- •2.3. Правило Крамера для решения невырожденных систем
- •2.4. Решение произвольных систем
- •2.5. Однородные системы линейных уравнений
- •3. Векторная алгебра и аналитическая геометрия.
- •3.1. Векторы
- •3.2 Линейная зависимость и независимость
- •3.3. Прямая на плоскости. Общее уравнение прямой
- •3.4 Уравнение прямой с угловым коэффициентом и некоторые другие уравнения прямой на плоскости
- •3.5. Взаимное расположение прямых на плоскости
- •3.6. Расстояние от точки до прямой на плоскости.
- •3.7. Уравнения плоскости в пространстве
- •3.8. Прямая в пространстве
- •3.9. Системы линейных неравенств
- •4. Пределы
- •4.1. Множества, операции над множествами
- •4.2. Предел функции
- •4.3. Основные теоремы о пределах
- •4.4. Непрерывность функции и вычисление простейших пределов
- •4.5 Раскрытие неопределенностей
- •4.6. Замечательные пределы
- •5. Производная и дифференциал.
- •5.1. Определение производной функции
- •5.2. Основные правила вычисления производных.
- •5.3 Таблица производных основных элементарных функций
- •5.4. Примеры вычисления производных.
- •5.5. Дифференциал функции
- •5.6. Связь производной и дифференциала.
- •5.7. Правило Лопиталя для раскрытия неопределенностей
- •6. Приложения производной.
- •6.1. Монотонность, экстремумы
- •6.2. Выпуклость
- •6.3. Асимптоты графика функции
- •6.4 Полное исследование функции и построение её графика.
- •6.5. Наименьшее и наибольшее значения функции
- •6.6 Экономическая интерпретация первой производной (предельный анализ)
- •6.7 Эластичность функций
- •7. Функции нескольких переменных
- •7.1. Основные определения.
- •7.2. Предел и непрерывность
- •7.3. Частные производные функции нескольких переменных
- •7.4. Дифференциал функции нескольких переменных
- •7.5. Частные производные второго порядка
- •7.6. Производная по направлению и градиент
- •7.7. Экстремум функции двух переменных
- •Вопросы к зачету
- •Тема 1. Матрицы и определители
- •Тема 2. Системы линейных алгебраических уравнений (слау)
- •Тема 3. Векторы, n-мерное векторное пространство
- •Тема 4. Аналитическая геометрия на плоскости
- •Тема 5. Предел и непрерывность функции
- •Тема 6. Производная и дифференциал
- •Тема 7. Приложения производной
- •Тема 8. Функции нескольких переменных
- •Задачи и примеры для подготовки к зачету
- •Контрольная работа № 1
- •Требования по оформлению контрольной работы
- •Рекомендуемая литература основная
- •Дополнительная
- •Содержание
- •1.Элементы линейной алгебры. 4
- •Высшая математика
- •Часть 1
Тема 7. Приложения производной
Исследование функций на монотонность.
Исследование функций на экстремум, необходимые и достаточные условия.
Исследование функций на выпуклость и вогнутость, точки перегиба.
Асимптоты графика функции.
Полное исследование функции и построение графика.
Нахождение наибольшего и наименьшего значения функции на замкнутом отрезке.
Предельный анализ в экономике.
Эластичность функций.
Тема 8. Функции нескольких переменных
Определение функции нескольких переменных. Область определения и область значений.
Линии и поверхности уровня.
Частные производные функции нескольких переменных.
Полный дифференциал функции нескольких переменных.
Производная по направлению и градиент.
Исследование на экстремум функции двух переменных.
Задачи и примеры для подготовки к зачету
1. Вычислить определители второго
порядка:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() д)
д)
![]() .
.
2. Решить уравнение:
![]() .
.
3. Решить системы двух уравнений с двумя
неизвестными по правилу Крамера:
а)
![]() б)
б)
![]() в)
в)
![]()
4. При каких значениях параметра
система имеет единственное решение:
![]()
5. Вычислить определители третьего
порядка разложением по первой строке
- а), б) и первому столбцу - в), г):
а)
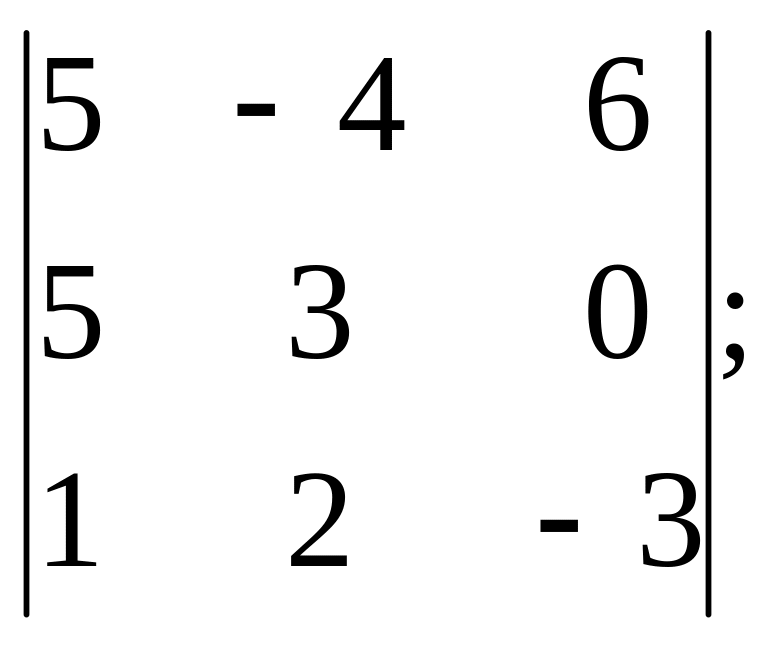 б)
б)
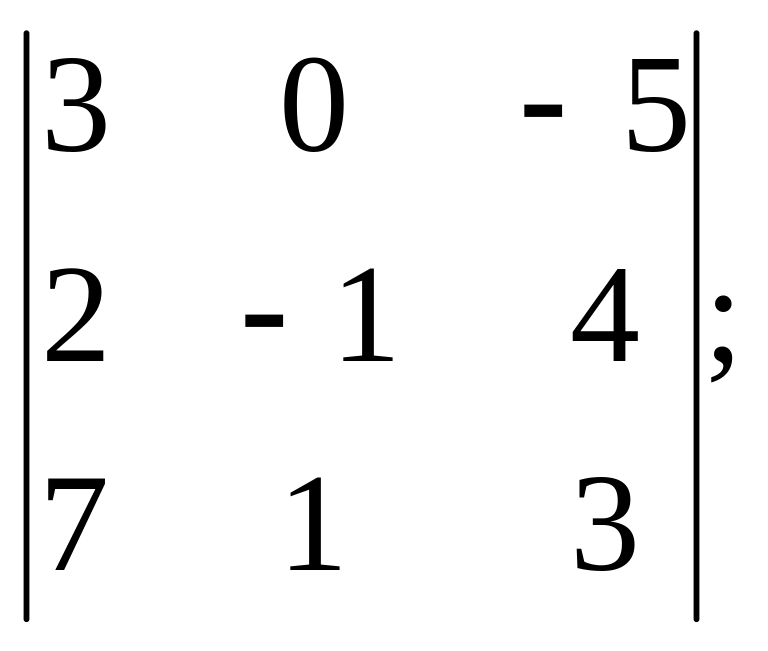 в)
в)
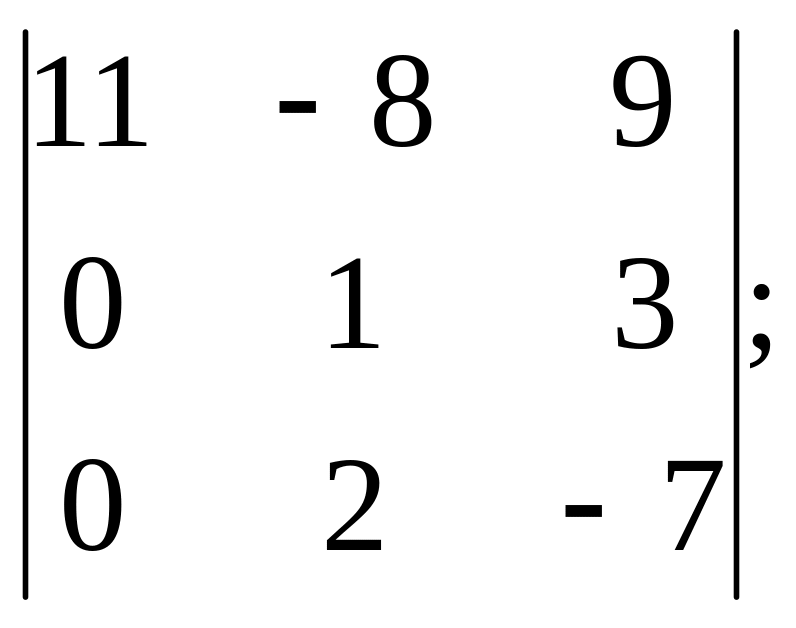 г)
г)
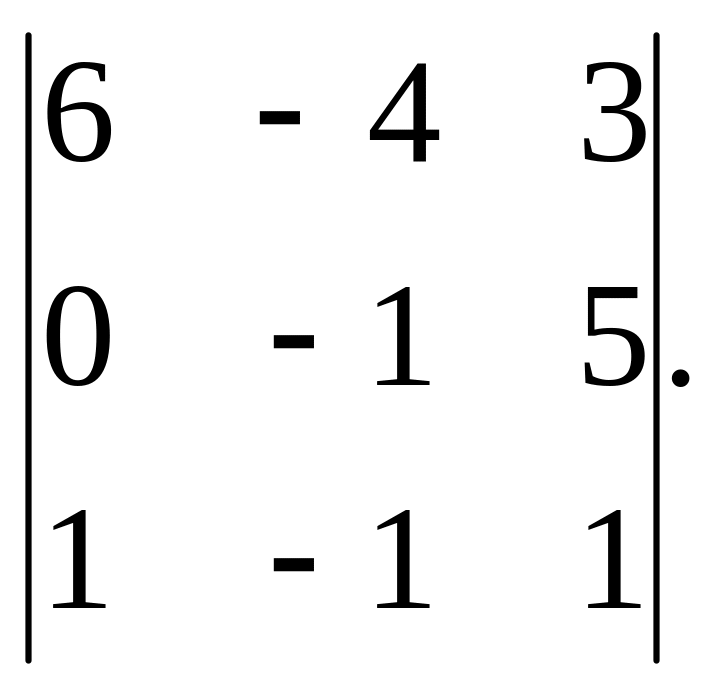
6. Вычислить определители третьего
порядка с помощью « правила треугольников»:
а)
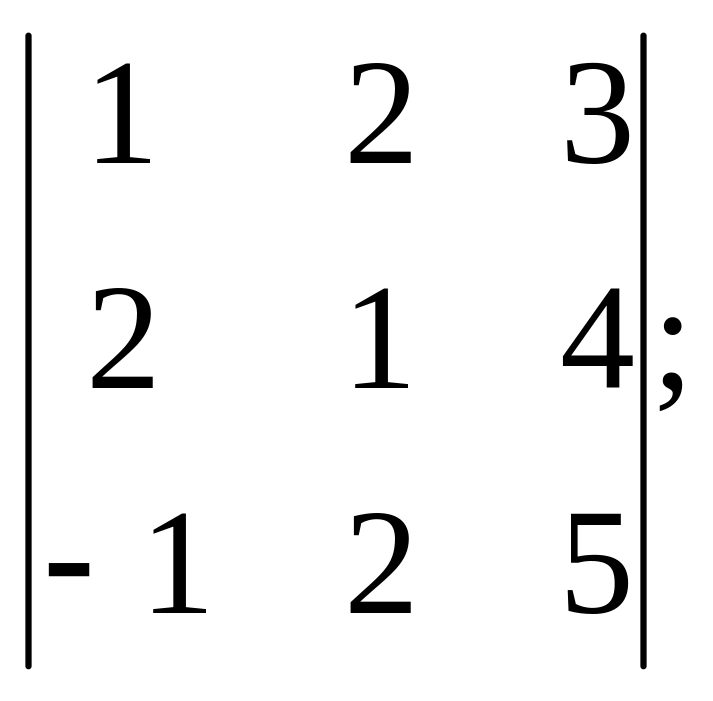 б)
б)
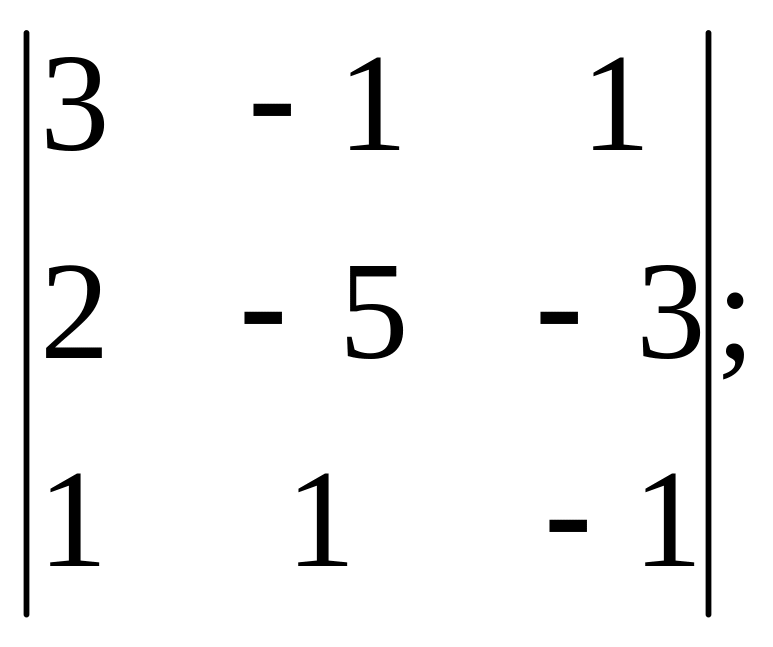 в)
в)
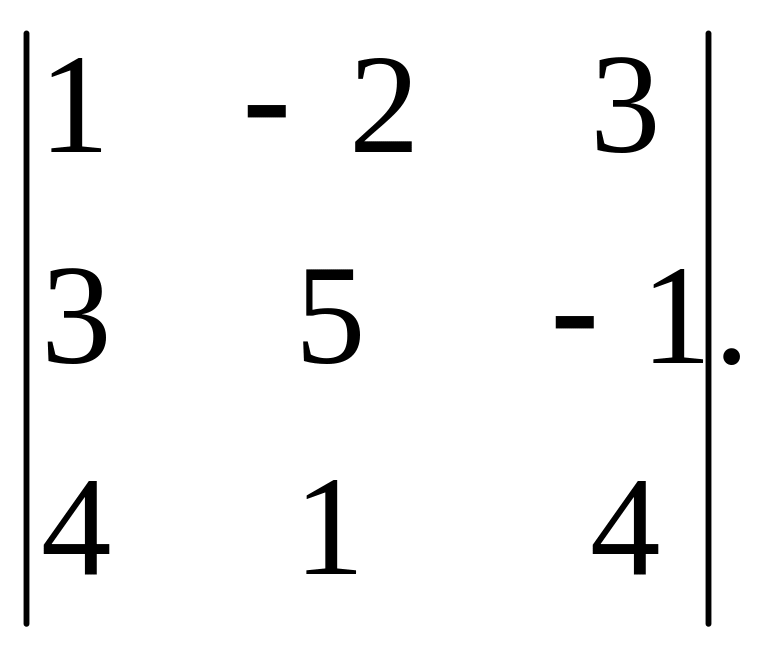
7. Вычислить определители третьего
порядка методом разложения по какой-нибудь
строке или столбцу: а) б)
б)
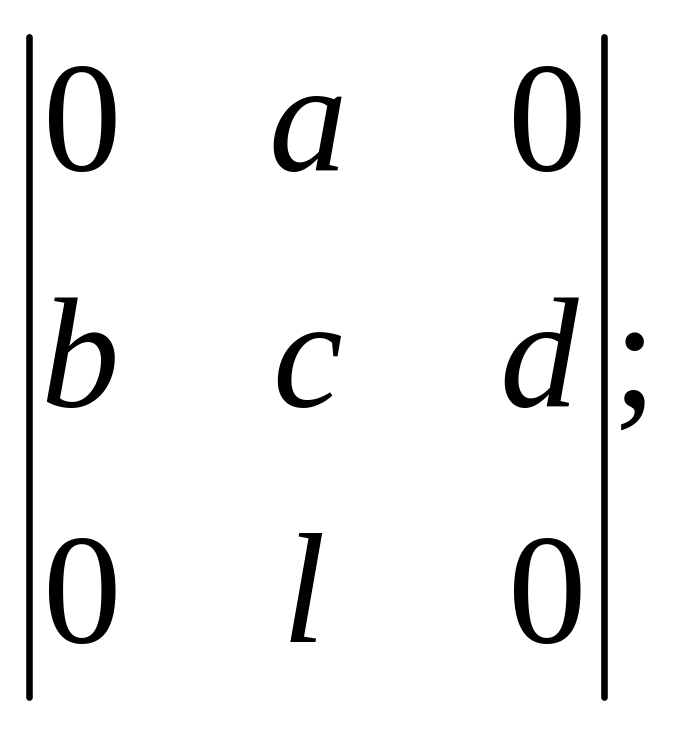 в)
в)
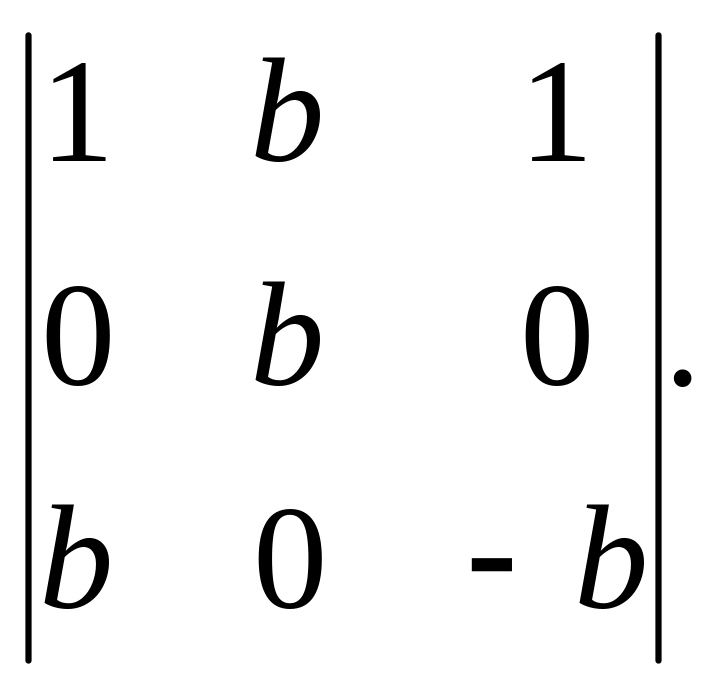
8. Используя метод разложения определителя
по элементам любой строки или любого
столбца, вычислить определители: а)
 б)
б)

9. Решить по правилу Крамера следующие
системы уравнений:
а)
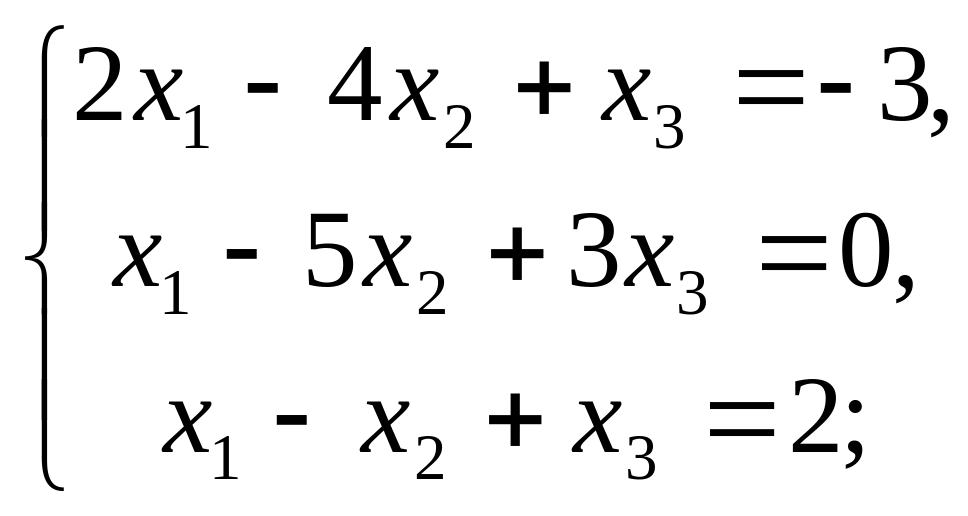 б)
б)
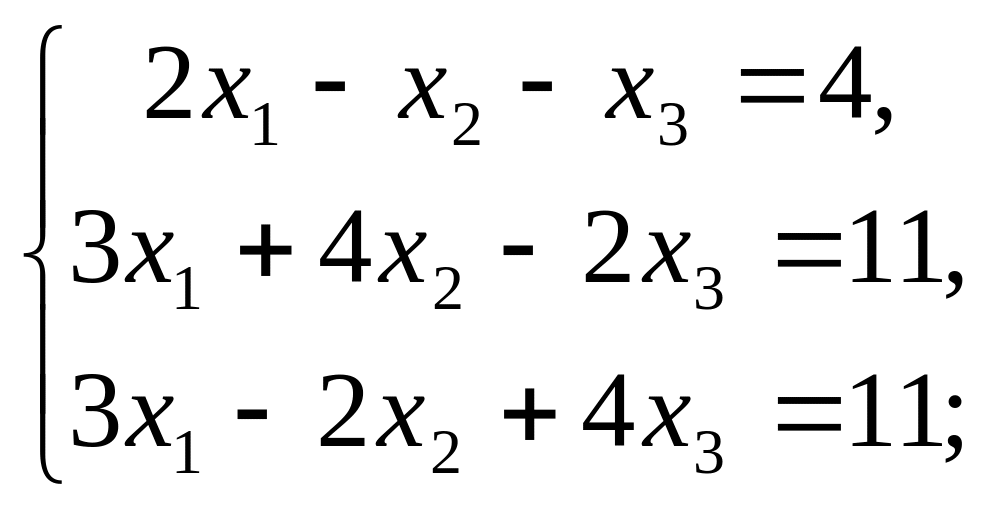 в)
в)
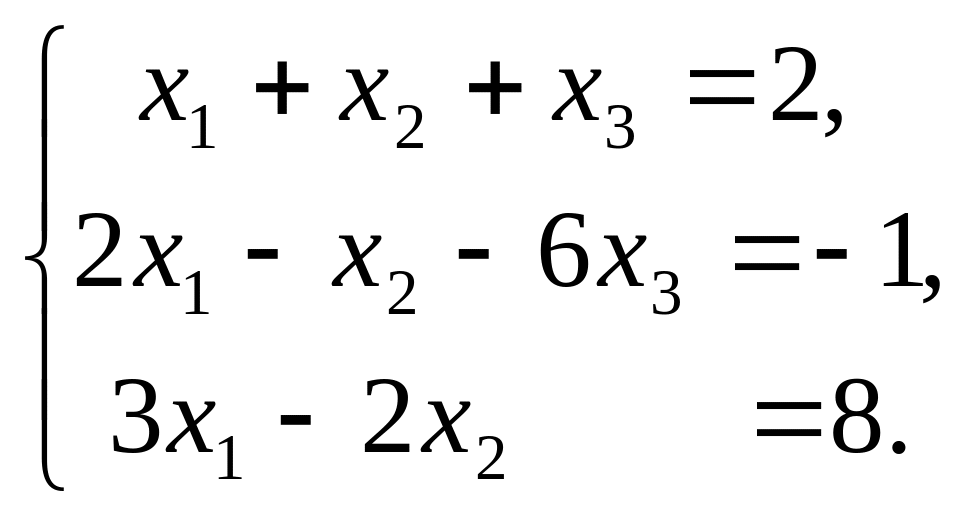
10. Элементами квадратной матрицы
третьего порядка являются числа
![]() .
Требуется: а) составить матрицу
;
б) транспонировать эту матрицу.
.
Требуется: а) составить матрицу
;
б) транспонировать эту матрицу.
11. Составить диагональную матрицу
третьего порядка, элементами главной
диагонали которой являются числа
![]() (при
(при
![]() ).
).
12. Найти матрицу
![]() ,
которая является линейной комбинацией
матриц
,
которая является линейной комбинацией
матриц
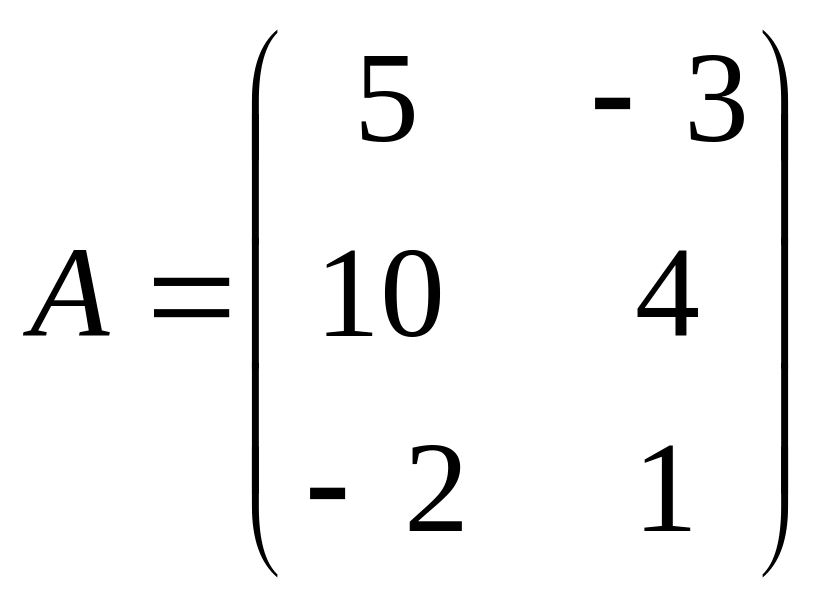 и
и
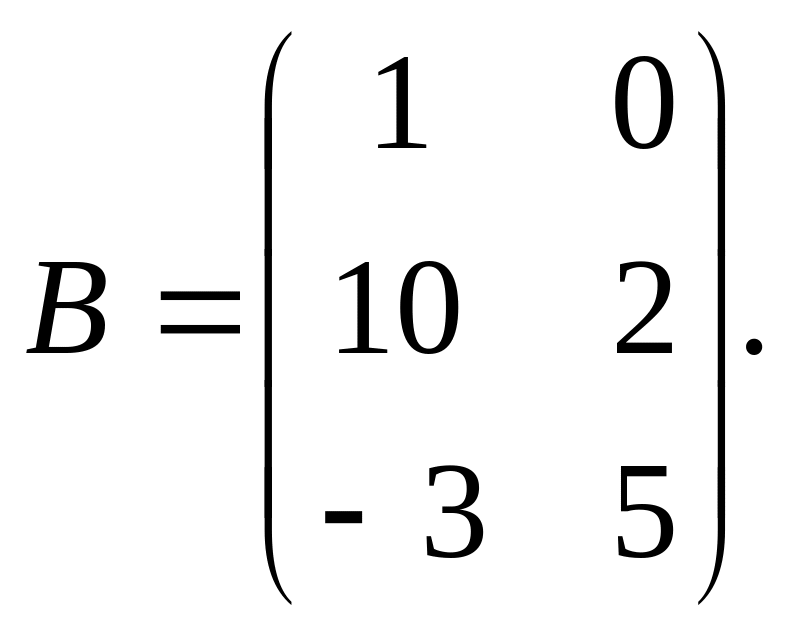
13. Найти линейную комбинацию
![]() матриц
матриц
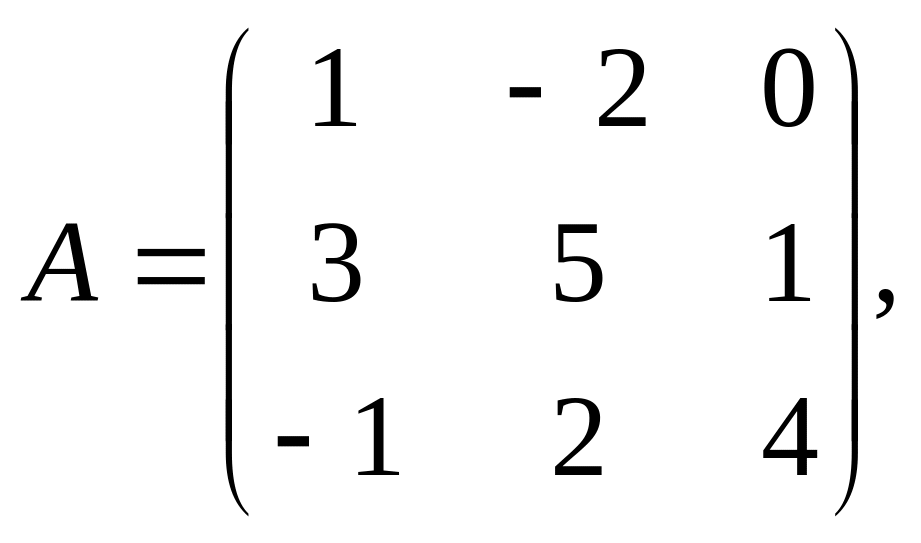
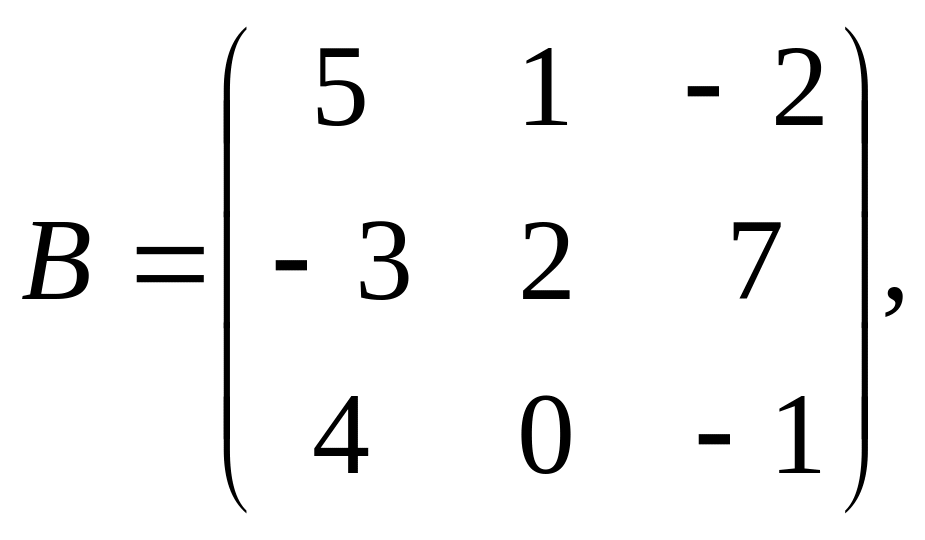
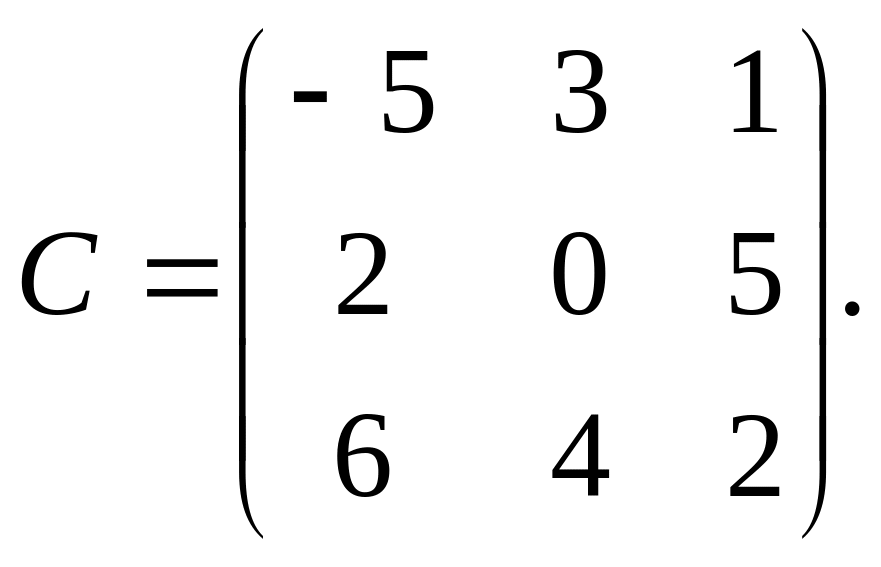
14. Проверить, являются ли данные матрицы
и
перестановочными: а)
![]() б)
б)
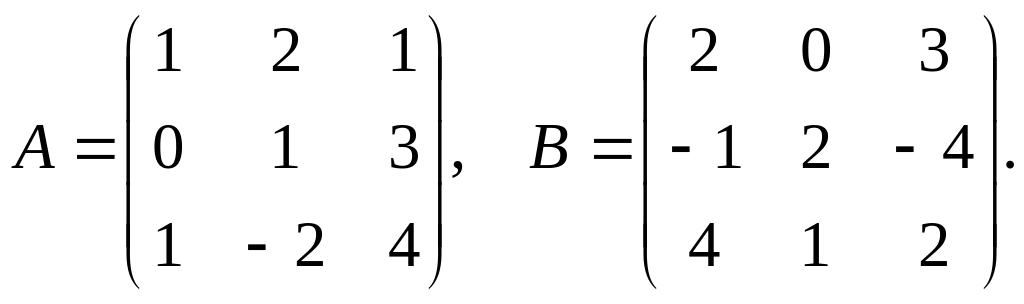
15. Вычислить произведение двух матриц:
а)
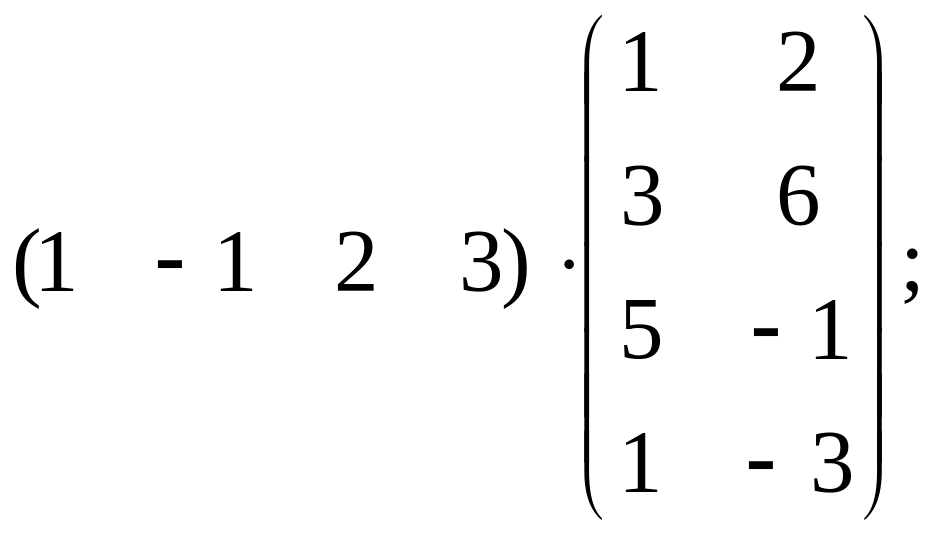 б)
б)
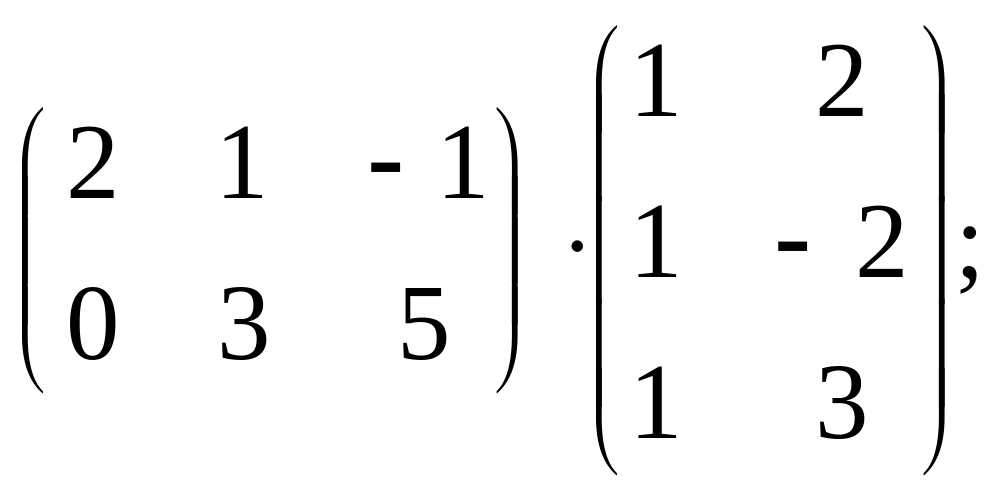 в)
в)
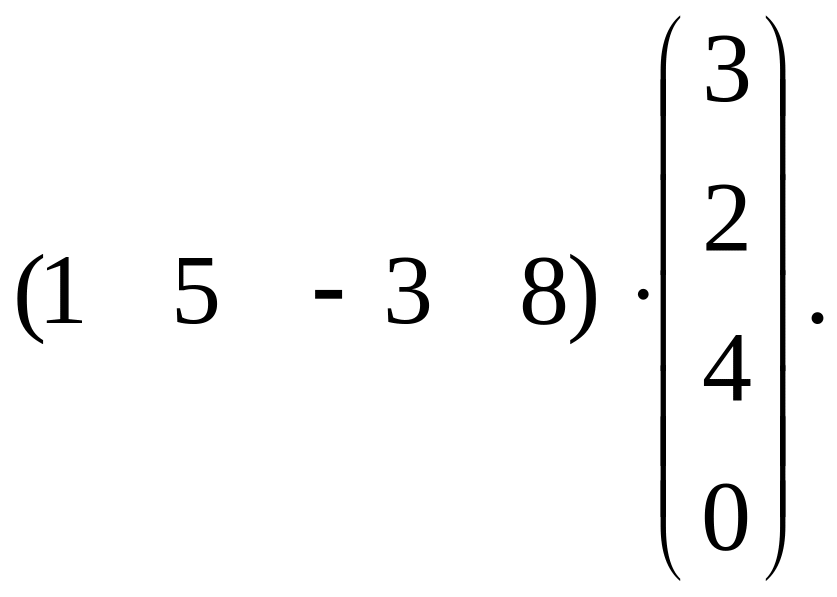
16. Найти матрицу
обратную
для матрицы
если: а)
![]() ;
б)
;
б)
![]() в)
в)
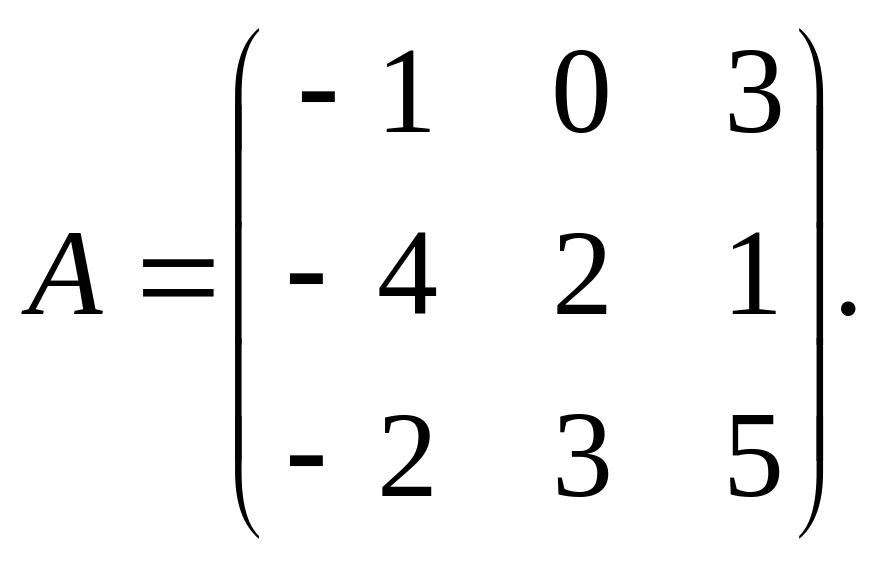
17. Решить матричные уравнения:
а)
![]() б)
б)
![]() в)
в)
![]()
18. Решить матричные уравнения:
а)
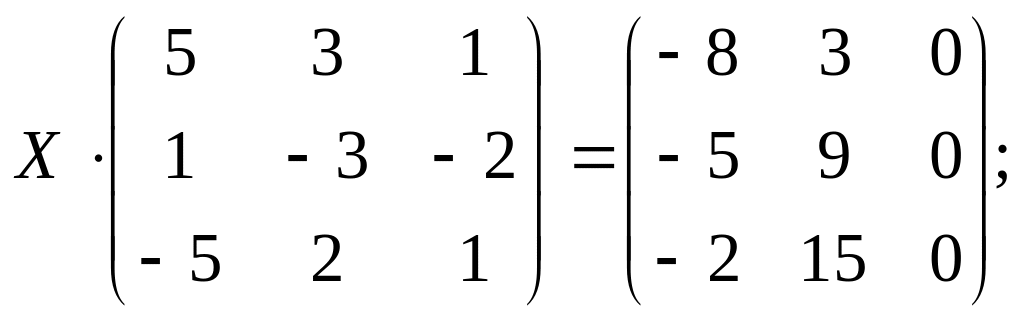 б)
б)
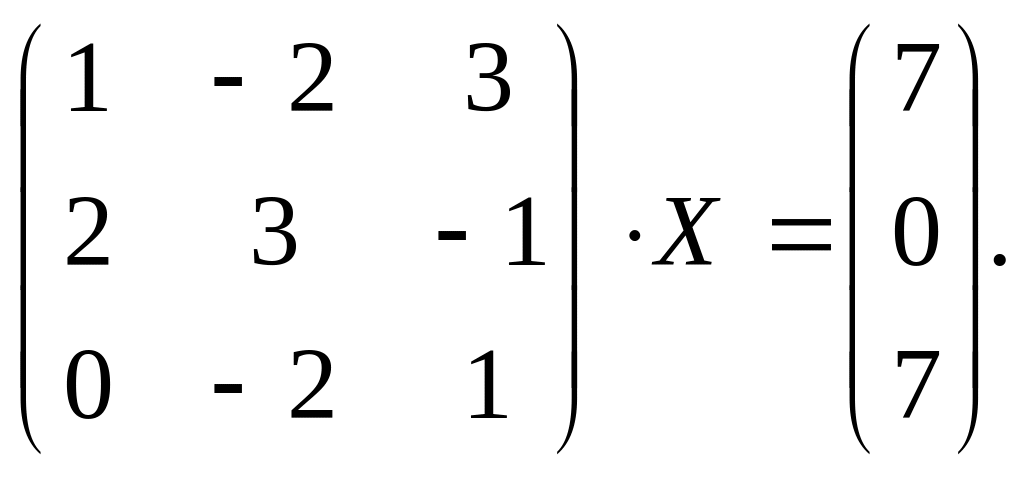
19. Решить следующие системы уравнений
матричным методом: а)
![]() б)
б)
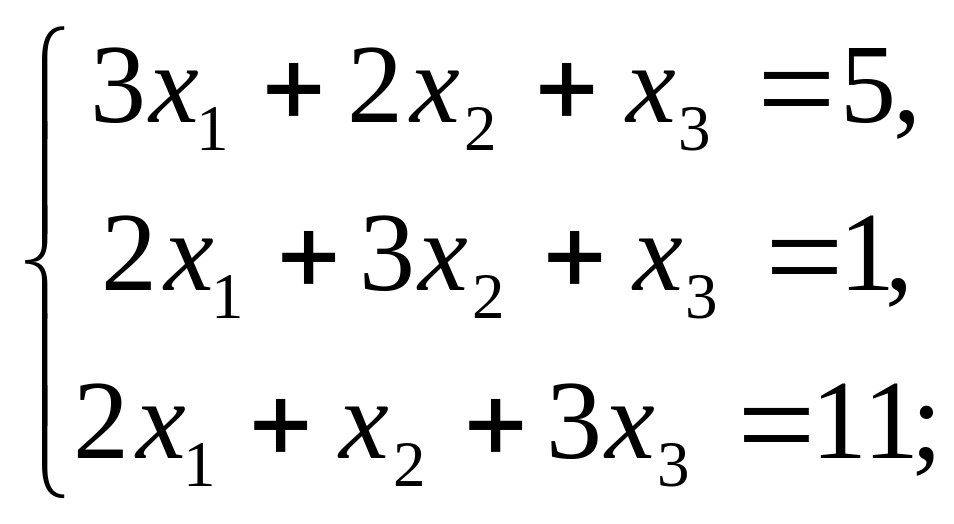 в)
в)
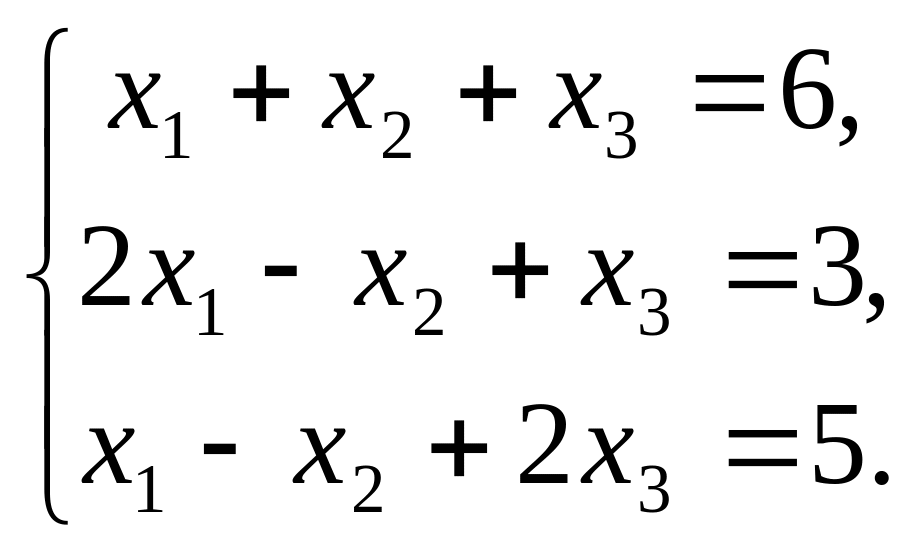
20. Решить следующие системы методом
Гаусса:
а)
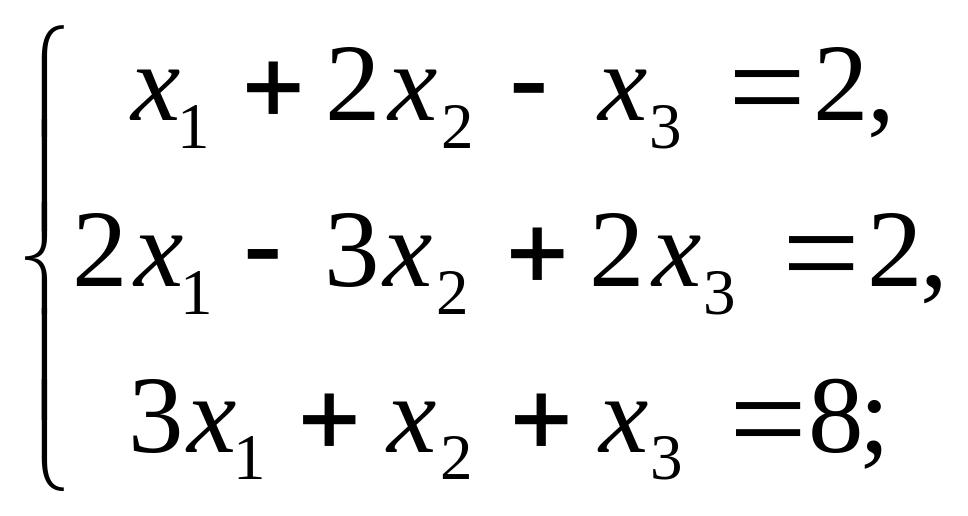 б)
б)
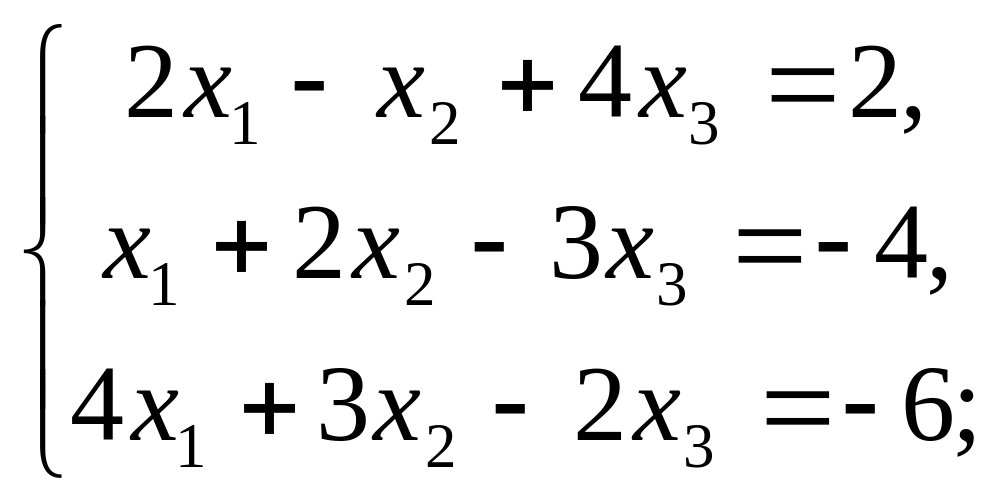 в)
в)
![]()
21. На плоскости
![]() построить области, координаты точек
которых удовлетворяют следующим
системам линейных неравенств:
а)
построить области, координаты точек
которых удовлетворяют следующим
системам линейных неравенств:
а)
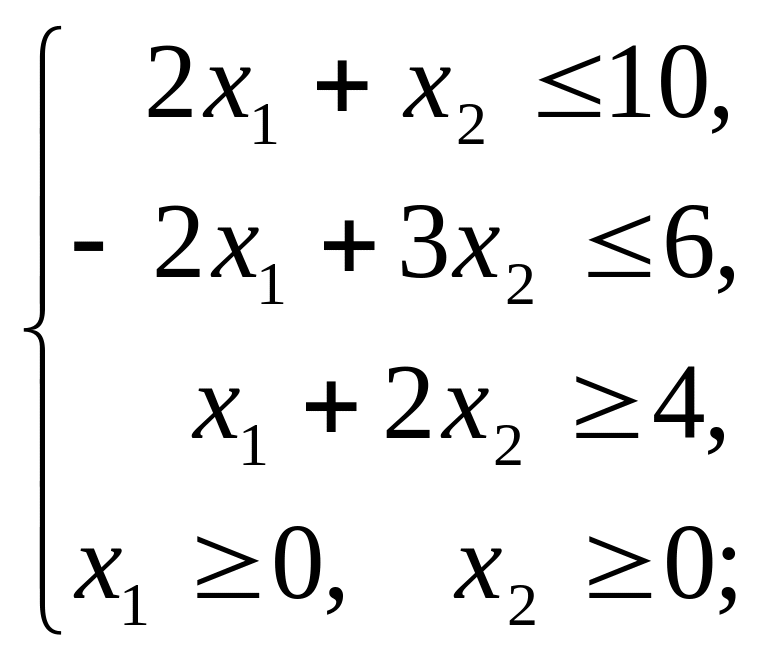 б)
б)
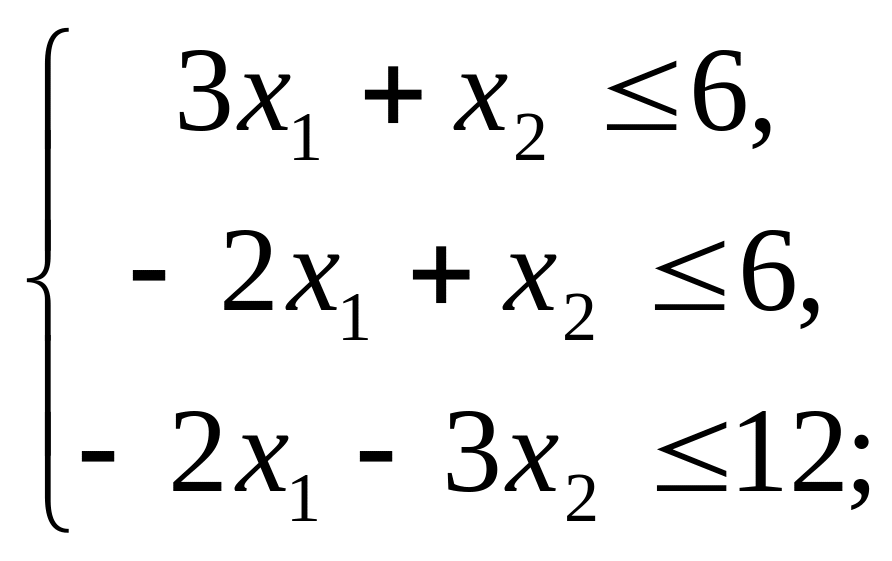 в)
в)
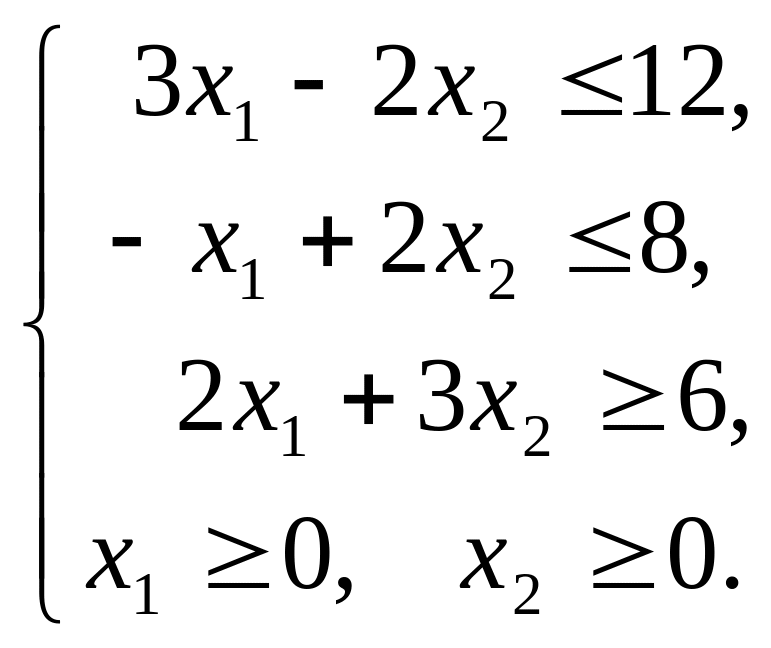 .
.
22. Показать, что векторы
![]() и
и
![]() образуют базис двухмерного пространства
и найти координаты вектора
образуют базис двухмерного пространства
и найти координаты вектора
![]() в этом базисе.
в этом базисе.
23. При каком значении параметра
векторы
![]() и
и
![]() -
перпендикулярны, найти длину вектора
-
перпендикулярны, найти длину вектора
![]() .
.
24. Найти угол между векторами
![]() и
и
![]()
25. Вычислить
![]() ,
где
,
где
![]()
![]()
![]() .
.
26. Дана прямая
![]() .
Определить угловой коэффициент
прямой: а) параллельной данной
прямой; б) перпендикулярной к данной
прямой
.
Определить угловой коэффициент
прямой: а) параллельной данной
прямой; б) перпендикулярной к данной
прямой
27.. Найти точку пересечения двух прямых
![]() и
и
![]() .
.
28. Дана прямая
![]() .
Составить уравнение прямой, проходящей
через точку
.
Составить уравнение прямой, проходящей
через точку
![]() :
а) параллельно данной прямой; б)
перпендикулярно к данной прямой.
:
а) параллельно данной прямой; б)
перпендикулярно к данной прямой.
29. Даны вершины треугольника
![]() ,
определить: а) величину угла
;
б) длину стороны
,
определить: а) величину угла
;
б) длину стороны
![]() ;
в) длину высоты, опущенной из вершины
;
г) уравнение прямой, проходящей через
вершину
,
параллельно стороне
;
д) площадь треугольника.
;
в) длину высоты, опущенной из вершины
;
г) уравнение прямой, проходящей через
вершину
,
параллельно стороне
;
д) площадь треугольника.
30. Найти проекцию точки
![]() на прямую, проходящую через точки
на прямую, проходящую через точки
![]() и
и
![]() .
.
31. Определить угол
,
образованный двумя прямыми:
![]() и
и
![]() .
.
32. Найти расстояние между двумя
параллельными прямыми:
![]() и
и
![]() .
.
33. Доказать, что прямая
![]() пересекает отрезок, ограниченный
точками
пересекает отрезок, ограниченный
точками
![]() и
и
![]() .
.
34. Составить уравнение плоскости,
которая проходит через точку
![]() и имеет нормальный вектор
и имеет нормальный вектор
![]() .
Найти расстояние от точки
.
Найти расстояние от точки
![]() до этой плоскости.
до этой плоскости.
35. Найти объединение и пересечение
двух множеств
![]() и
и
![]() .
.
36. Найти пределы: а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() д)
д)
![]() е)
е)
![]()
37. Раскрыть неопределенности с помощью
первого замечательного предела:
а)
![]() б)
б)
![]() в)
в)
![]()
38. Раскрыть неопределенности с помощью
второго замечательного предела:
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() .
.
39. Найти производные следующих функций:
а)
![]() ;
б)
;
б)
![]() в)
в)
![]() г)
г)
![]() д)
д)
![]() е)
е)
![]() .
.
40. Составить уравнения касательных к
графикам функций: а)
![]() - в точках пересечения с осями координат;
б)
- в точках пересечения с осями координат;
б)
![]() в точке пересечения с осью
в точке пересечения с осью
![]() .
.
41. Раскрыть неопределенности с помощью
правила Лопиталя: а)
![]() б)
б)
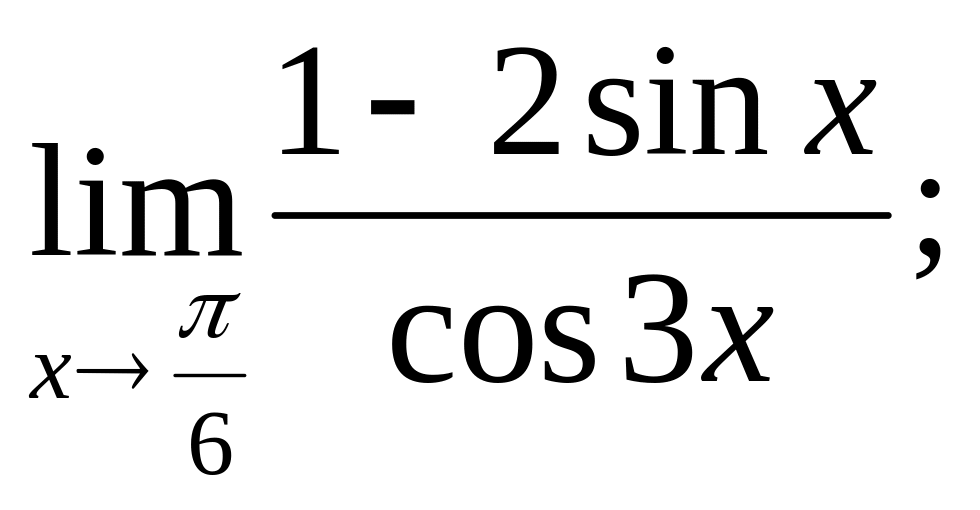 в)
в)
![]() г)
г)
![]() д)
д)
![]()
42. Исследовать на экстремум функции:
а)
![]() б)
б)
![]() .
.
43. Найти наибольшее и наименьшее значения
функции на заданном отрезке: а)
![]() б)
б)
![]() в)
в)
![]()
44. Провести полное исследование функций
и построить их графики: а)![]() б)
б)
![]() в)
в)
![]()
45. Найти эластичность спроса по цене
и дать экономическую интерпретацию,
если функция спроса имеет вид: а)
![]() при
при
![]() б)
б)
![]() при
при
![]()
46. Построить линии уровня следующих
функций:
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() .
.
47. Найти частные производные следующих
функций: а)
![]() б)
б)
![]() в)
в)
![]() ;
г)
;
г)
![]() .
.
48. Найти градиенты функций в указанных
точках:
а)
![]() б)
б)
![]() в)
в)
![]()
49. Найти частные производные второго
порядка от функций:
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
50. Найти экстремумы функций: а)
![]() б)
б)
![]()
