7.6. Производная по направлению и градиент

Частные производные функции нескольких переменных, по своему смыслу, характеризуют скорость изменения функции по направлениям осей координат. Вполне естественно выяснить с какой скоростью изменяется функция в данной точке в фиксированном направлении, задаваемом вектором . Ответ на этот вопрос дает понятие производной в точке по направлению вектора . Опуская точное определение такой производной, которая естественно является пределом отношения приращения функции к приращению аргумента, вычисленному в заданном направлении, приведем формулы для её вычисления.

Для дифференцируемой функции трех переменных , производная в направлении вектора :

, где - направляющие косинусы вектора , которые вычисляются по формулам , , и являются координатами единичного вектора того же направления: .

Для дифференцируемой функции двух переменных формулы аналогичны, только будет отсутствовать третья координата.

Определение. Градиентом функции называется вектор , координаты которого равны соответственно частным производным и в точке , то есть .

Для функции трех переменных имеем .

Используя определение градиента, формулы для вычисления производной по направлению можно записать в виде скалярного произведения двух векторов:

или

Из этих формул, с учетом определения скалярного произведения, , следуют основные свойства градиента:

• градиент это вектор, направленный в сторону максимального роста функции 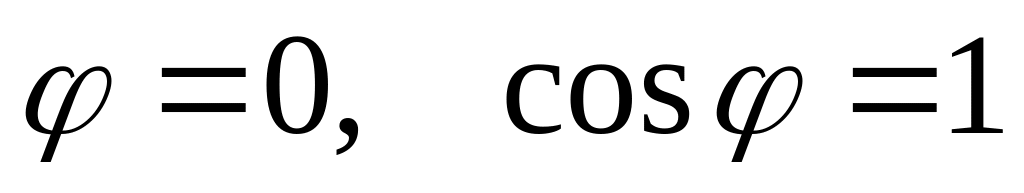, то есть производная по направлению в данной точке принимает максимальное значение в направлении её градиента в этой точке;

• модуль градиента равен максимальной производной по направлению.

• градиент перпендикулярен линии (поверхности) уровня функции;

Пример 1. Найти градиент функции и его модуль в точке , и вычислить производную по направлению вектора .

Решение.1)Вычисляем . Подставляя координаты точки , получим . Модуль, полученного вектора .

2) Вычисляем единичный вектор заданного направления . Производная по направлению равна = .

Пример 2. Найти вектор нормальный к линиям уровня функции .

Решение. Поскольку градиент функции перпендикулярен линиям уровня этой функции в произвольной точке, получим , значит, вектор - нормальный вектор к линиям уровня , которые образовывают множество параллельных прямых, перпендикулярных вектору .

7.7. Экстремум функции двух переменных

Определение. Точка является точкой максимума (минимума) функции , если существует окрестность этой точки такая, что для всех точек из этой окрестности ( ).

Максимум или минимум, как и ранее, называют экстремумом. Далее, в силу простоты и наглядности, исследование на экстремум проведем для функций двух переменных , тем более, что идеи и последовательность действий такие же, как и для функции одной переменной.

Прежде всего, находим стационарные точки, то есть точки в которых обращаются в нуль обе частные производные – необходимое условие экстремума, то есть решаем систему уравнений:

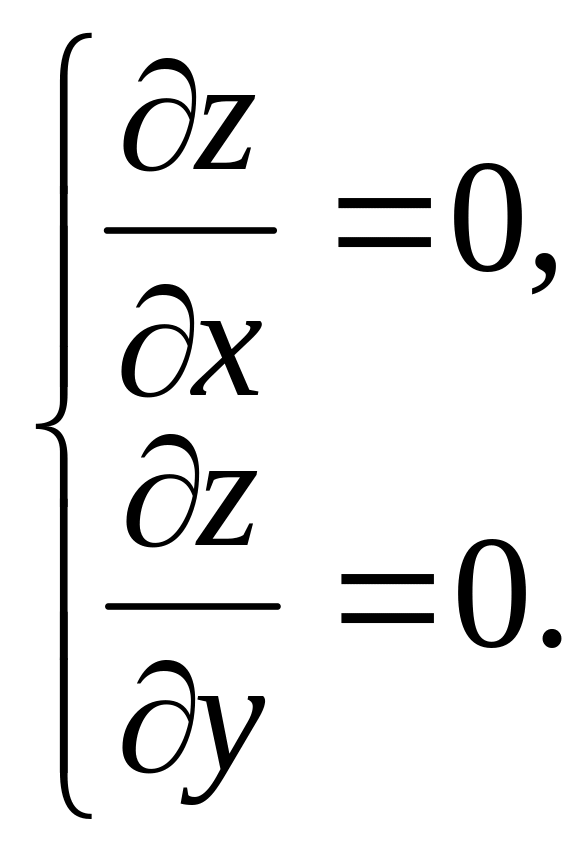
Пусть, например, точка является решением этой системы, то есть – стационарная точка. Для того, чтобы выяснить будет ли в этой точке экстремум, используем следующие достаточные условия существования экстремума в стационарной точке.

1) Находим частные производные второго порядка исследуемой функции и вычисляем их значения в точке , обозначая:

; ; .

2) Составим определитель

.

3) Если , то в точке будет экстремум:

• максимум, если

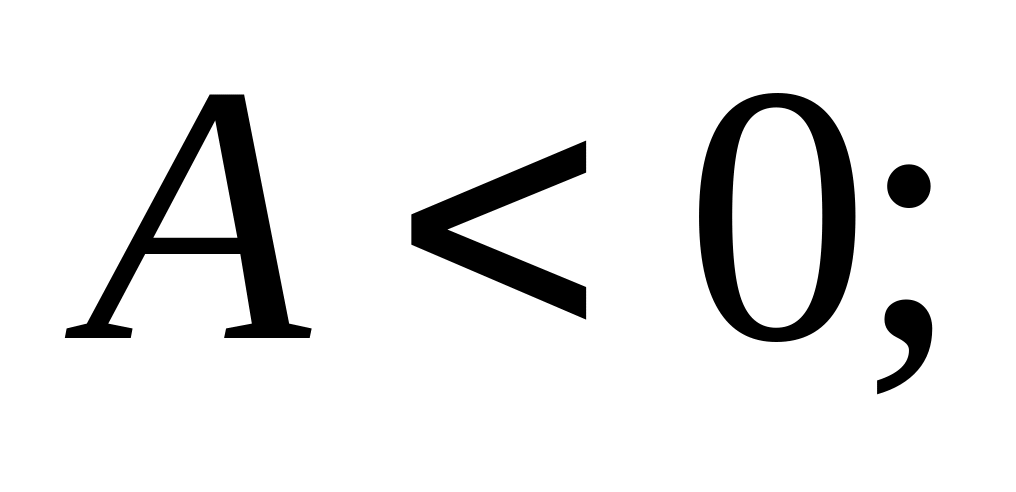
• минимум, если

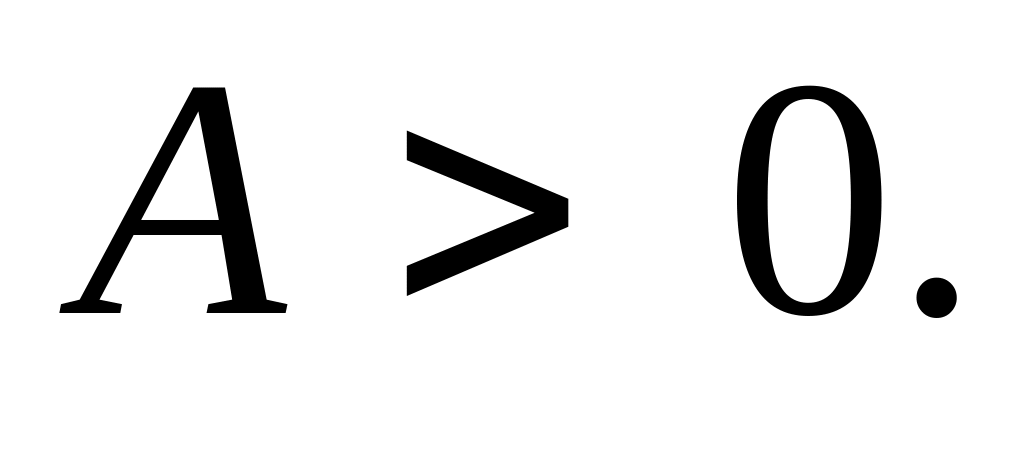
4) Если , то в точке нет экстремума.

5) Если , то требуется дальнейшее исследование.

Пример. Исследовать на экстремум функцию

Решение. 1) Ищем стационарные точки:

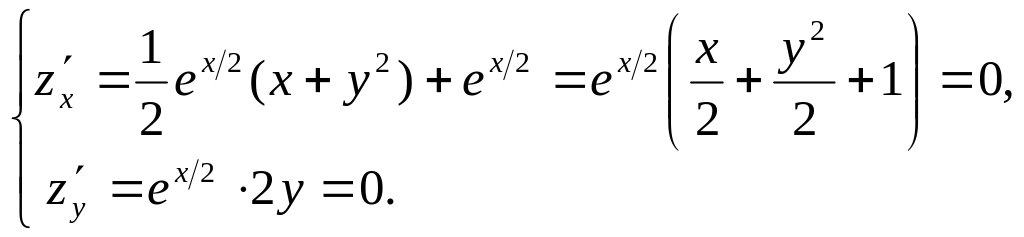
Из второго уравнения системы получим , подставляя это значение в первое уравнение, после очевидных вычислений имеем . Таким образом далее предстоит исследовать единственную стационарную точку .

2) Находим производные второго порядка данной функции:

; ; .

3) Вычисляем значения вторых производных в стационарной точке:

; ; .

4) Составляем определитель

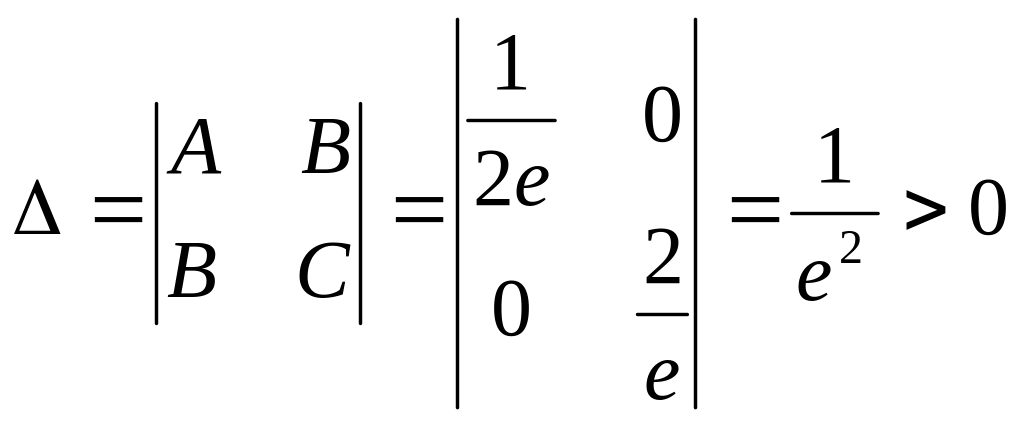, т.к. , то в точке есть экстремум, а так как , это минимум.

5) Находим .

Замечание. Исследование на наибольшее и наименьшее значение функции нескольких переменных непрерывной в замкнутой ограниченной области подобно исследованию функции одной переменной на замкнутом промежутке . Сначала ищутся критические точки внутри области и вычисляются значения функции в этих критических точках. Затем находят наибольшее и наименьшее значения функции на границе области. И в заключение, из всех полученных значений выбирают наибольшее и наименьшее, которые и являются решением задачи.