6.7 Эластичность функций

Одна из важнейших задач любого бизнеса – установление связи между изменениями цены на реализованную продукцию и доходом. Если фирма повышает цену на единицу продукции, это уменьшает объем продаж. Интуитивно понятно, что здесь важны не абсолютные изменения цены и количества продукции, а относительные, или, как говорят, процентные (есть разница - повысить цену на 1 руб., если исходная цена была 1000 руб. и если она была 1 руб.!). Для характеристики этих взаимоизменений в экономике вводится такое понятие как эластичность.

Если кривая спроса – это функция , где Р- цена единицы продукции, а Q – ее количество, то эластичность спроса от цены определяется как отношение:

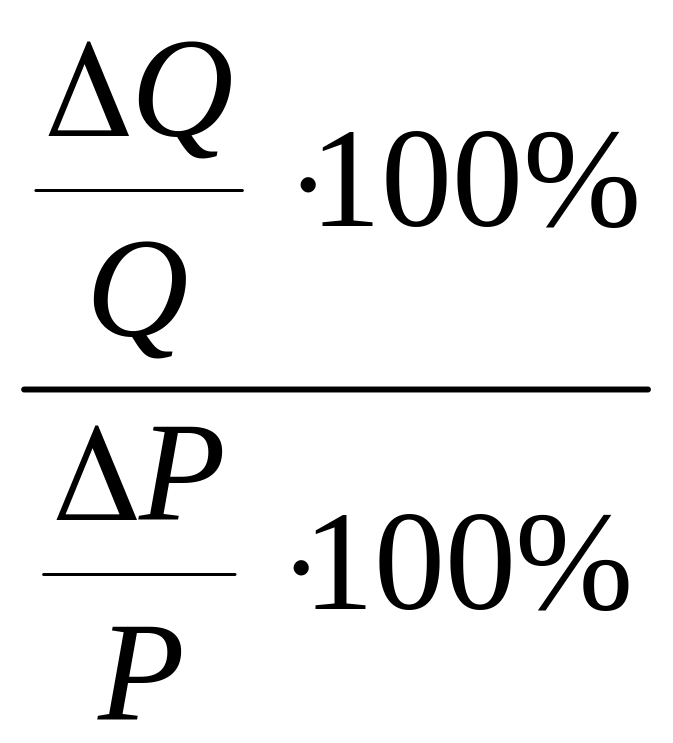= . Сокращая общий множитель 100%, окончательно получаем 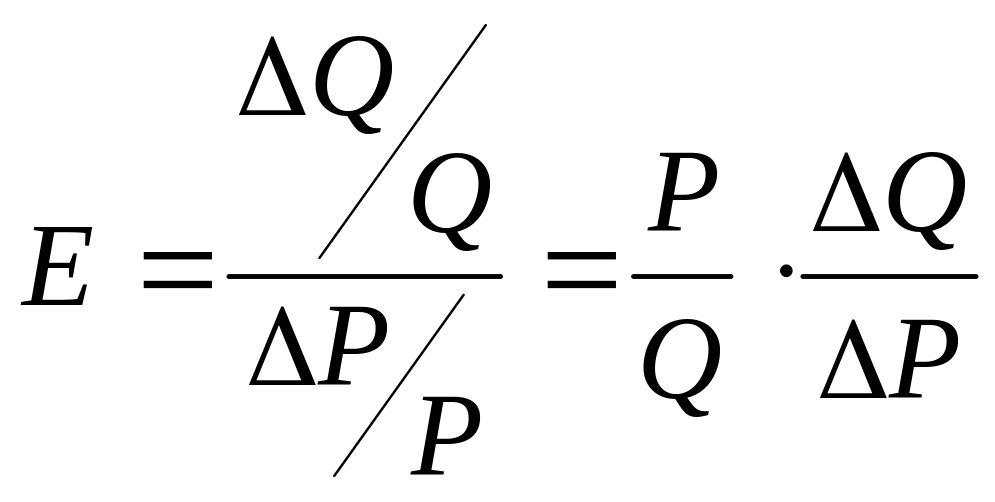. Вычисленная таким образом эластичность, называется дуговой эластичностью, т.е. средней на соответствующем участке кривой спроса

Переходя, как обычно, к пределу при , мы получаем выражение для точечной эластичности.

.

Эластичность спроса по цене, в данном случае, отражает, насколько процентов изменится спрос, если цена на товар изменится на 1%,и часто обозначается .

Поскольку, кривая спроса – функция убывающая, то , и в исследованиях, эластичность спроса от цены обычно берется по модулю, т.е. рассматривается ее положительное значение.

В зависимости от численных значений модуля эластичности спроса по цене различают товары эластичного и неэластичного спроса. В первом случае – эластичный спрос - повышению цены на 1% соответствует понижение спроса более чем на 1%, а понижение цены на 1% приводит к росту покупок более чем на 1%, модуль эластичности . Во-втором случае – неэластичный спрос – повышение цены на 1% влечет за собой понижение спроса менее чем на 1%, а уменьшение цены на 1% приводит к росту покупок менее чем на 1% , модуль эластичности .

Аналогично вводятся эластичности других экономических функций.

Пример. Найти эластичность спроса по цене при Р=2, если функция спроса имеет вид .

Решение. Ищем производную от функции , .

Тогда эластичность спроса по цене равна . При Р=2 получаем . Это означает, что если цена возрастет на 1%, то спрос на товар уменьшится на 0,15%, то есть спрос неэластичный.

7. Функции нескольких переменных

7.1. Основные определения.

Во многих практических задачах изучаемая величина зависит от многих факторов, принимающих некоторые числовые значения, которые, в общем случае, можно обозначить . Задачи подобного рода наталкивают на мысль об изучении функций, зависящих от нескольких переменных.

Определение. Если задан закон, по которому каждому упорядоченному набору чисел из некоторого множества Х ставится в соответствие единственное действительное число , то говорят, что на множестве Х задана функция переменных, при этом пишут: .

. Множество Х называется областью определения функции , а множество значений .

Если числа считать координатами некоторой точки , то функция нескольких переменных будет функцией этой точки и записывается . Такая обобщенная запись позволяет изучать свойства функций независимо от количества переменных. Более того, основные свойства функции двух переменных, как наиболее простой аналитически и геометрически, естественным образом распространить на функции большего количества переменных. Поэтому далее мы будем рассматривать, в основном, функции двух и трех переменных.

Наиболее наглядна интерпретация функции для случая двух переменных. В этом случае - точка плоскости, и в соответствии с общепринятыми обозначениями, функция записывается в виде (в случае трех переменных - ). Областью определения функции , является некоторое множество точек плоскости; для функции трех переменных – множество точек пространства. Например, областью определения функции будет множество точек координаты которых удовлетворяют неравенству . Достаточно легко определить, что это первая и третья координатные четверти, включая оси координат.

Важной геометрической характеристикой функций двух и трех переменных являются линии и поверхности уровня. Линией уровня функции двух переменных называется множество точек плоскости в которых эта функция принимает одно и тоже значение, уравнение линий уровня , где . Аналогично, уравнение поверхностей уровня .