6.2. Выпуклость

Функция , называется выпуклой (выпуклой вниз) на интервале (а,b), если ее график проходит выше любой своей касательной на этом интервале, и вогнутой (выпуклой вверх) - ниже. Для ориентировки и запоминания отметим, что в первом случае функция ведет себя как функция , а во-втором случае как

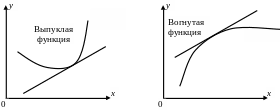
Выпуклая функция с увеличением х растет все быстрее, т.е. скорость роста возрастает (ускорение - положительно). Вогнутая функция, с увеличением растет медленнее ( - отрицательно).

Таким образом, проясняется роль второй производной в определении участков выпуклости и вогнутости функций: - влечет за собой выпуклость функции на соответствующем участке, - вогнутость. Обратите внимание, что вторая производная от функции равна , а для функции .

Точки, в которых выпуклость функции меняется на вогнутость или наоборот, называются точками перегиба. Очевидно, что в этих точках вторая производная обращается в нуль или не существует, в частности равна бесконечности - критические точки второй производной. Поскольку эти условия лишь необходимые для существования точек перегиба, то в критических точках может быть перегиб, но может его и не быть!

К достаточным условиям приводят рассуждения полностью аналогичные рассуждениям по исследованию функции на экстремум, только там мы работали с первой производной, а здесь со второй. Ниже приводим схему исследования функции на выпуклость и вогнутость.

1. Находим область определения функции.

2. Ищем вторую производную и критические точки второй производной.

3. Критические точки разбивают числовую ось на участки знакопостоянства второй производной, т.е. на участки постоянной выпуклости и вогнутости.

4. Анализируем критические точки на предмет смены знака второй производной при переходе через каждую из них и делаем вывод, является ли они абсциссами точек перегиба.

5. Вычисляем ординаты точек перегиба.

Пример: Найти точки перегиба функции .

Решение. Находим вторую производную и приравниваем её к нулю: . Квадратное уравнение имеет два корня, которые являются критическими точками второй производной ( подозрительными на точки перегиба) : . Определяем знаки второй производной в каждом из получившихся интервалов, и делаем вывод о выпуклости и вогнутости функции в каждом интервале. При и вторая производная и функция на каждом из этих бесконечных интервалов - вогнутая. На интервале вторая производная отрицательна и функция - выпуклая. Точки и являются абсциссами точек перегиба, так как при переходе через них вторая производная меняет знак. Ординаты этих точек равны .

6.3. Асимптоты графика функции

Определение. Асимптотой графика функции называется прямая , к которой стремится график функции, когда точка вдоль по графику стремится в бесконечность.

Асимптоты бывают вертикальные и наклонные .

Достаточно очевидны и понятны следующие два утверждения.

1). Если или , то прямая будет вертикальной асимптотой графика функции .

2). Если существуют конечные пределы и , то прямая будет наклонной асимптотой графика функции .

Следует иметь в виду, что пределы могут быть разные при и , а это означает, что и асимптоты могут быть разные на «плюс бесконечности» и на «минус бесконечности».