5.7. Правило Лопиталя для раскрытия неопределенностей

Пусть нам требуется раскрыть неопределенность , причем функции и дифференцируемые в некоторой окрестности точки а. Поскольку, в точке а выполняется равенство , преобразуем данный предел следующим образом 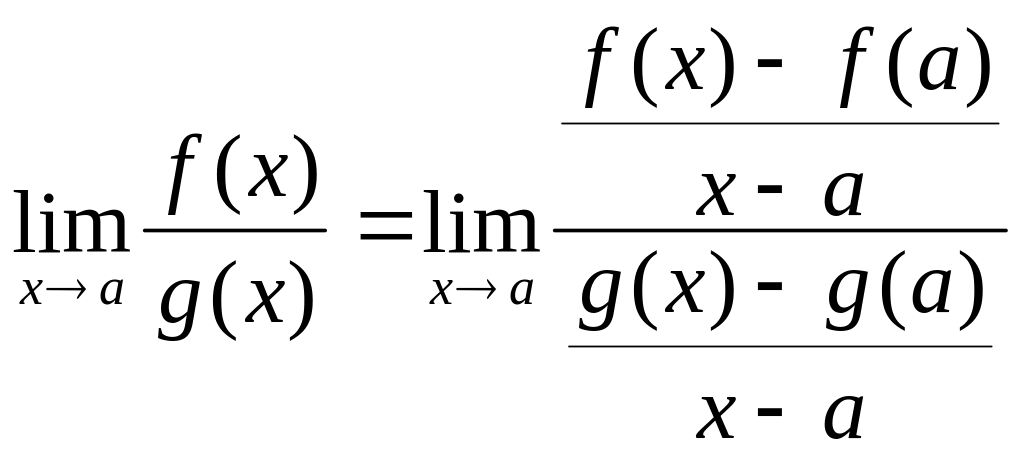= 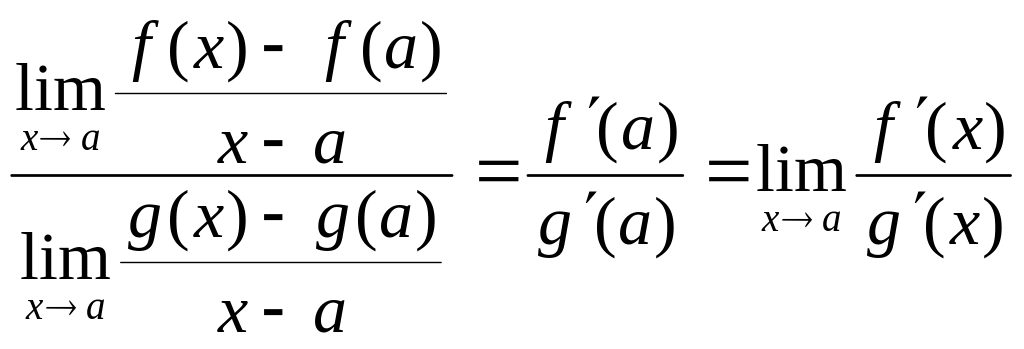, если предел отношения производных существует и . Это, конечно, не доказательство, но идея вычисления пределов с помощью производных достаточно очевидна и влечет за собой справедливость правила Лопиталя:

, для дифференцируемых функций, при раскрытии неопределенности «ноль на ноль», предел отношения функций равен пределу отношения их производных, при условии, что последний предел существует.

Пример. Вычислить предел .

Решение. Легко видеть, что числитель и знаменатель дроби равен нулю при значении аргумента , поэтому, предполагая, что предел отношения производных существует, применяем правило Лопиталя.

.

Замечание 1. Правило Лопиталя работает в такой же форме и для раскрытия неопределенностей , то есть, если существует предел отношения производных, то

.

Замечание 2. На практике встречаются неопределенности и других видов, но они легко сводятся к уже рассмотренным. Например, .

При раскрытии неопределенностей выручает предварительное логарифмирование, так вместо выражения рассматривается , что во всех перечисленных случаях дает неопределенность вида . Тогда, если , то исходный предел .

6. Приложения производной.

6.1. Монотонность, экстремумы

Функция монотонно возрастает (убывает) на промежутке , если для любых , из следует . То есть, если большему значению аргумента соответствует большее значение функции, то функция возрастает, если меньшее – убывает.

Достаточно очевидно следующее правило: если для любых , то функция возрастает на этом интервале, если же , то - убывает. Другими словами, скорость изменения положительна – функция растет, отрицательна – убывает.

Точки, в которых производная обращается в нуль, либо не существует, в частности равна бесконечности (необходимые условия экстремума) , называются точками подозрительными на экстремум или критическими точками. В этих точках функция может принимать максимальное или минимальное (экстремальное) значение, но может и не принимать. Классический пример функция равная нулю в т. х=0. Её производная , также равна нулю в нуле, а экстремума, тем не менее, нет, поскольку в любой окрестности нуля будут как положительные значения функции, так и отрицательные, т.е. не может быть ни максимальным, ни минимальным значением рассматриваемой функции. Экстремум наверняка будет существовать в критической точке , если при переходе через эту точку меняется направление её монотонности, т.е. в некоторой окрестности точки производная будет иметь разные знаки слева и справа от этой точки. Это утверждение носит название первого достаточного правила исследования функции на экстремум. Таким образом, при исследовании функции на монотонность и экстремум предлагается следующая последовательность действий.

1. Находим область определения функции.

2. Ищем первую производную и критические точки- точки, в которых производная обращается в нуль либо, не существует, в частности равна бесконечности.

3. Определяем знаки первой производной в каждом интервале, на которые разбивают критические точки область определения функции.

4. По знаку производной в каждом из интервалов делаем вывод о характере монотонности функции на этом интервале.

5. Применяя первое достаточное правило, делаем выводы о наличии экстремума и определяем характер этого экстремума в каждой критической точке.

6. Для точек, в которых существует экстремум, находим соответствующие экстремальные значения функции.

Замечание. В этом разделе мы ведем речь о, так называемых, локальных экстремумах, хотя прилагательное «локальный» зачастую опускается, считается естественным. Функция принимает в точке локальный максимум (минимум), ,если существует окрестность точки , такая, что для всех значений х из этой окрестности .

Пример. Исследовать на экстремум функцию .

Решение. Область определения функции вся числовая ось. Находим первую производную и приравниваем ее к нулю: . Полученное уравнение , имеет три корня: , которые являются критическими точками данной функции. Наносим их на числовую ось и определяем знаки производной в каждом из получившихся интервалов и делаем выводы о характере монотонности функции в этих интервалах (см. рисунок)

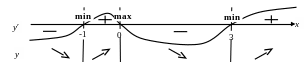
В результате получаем три экстремальные точки .