4.5 Раскрытие неопределенностей
Для непрерывных функций, вычисление
предела труда не составляет, предел
равен значению функций в предельной
точке. Но как поступить, если, например,
функция - дробь, числитель и знаменатель
которой в предельной точке равны нулю.
В этом случае говорят, что имеется
неопределенность
,
и задача вычисления предела заключается
в выяснении, что же все- таки кроется за
этой неопределенностью. Дело в том, что
предел в этом случае может равняться
0, конечному числу, бесконечности или
вовсе не существовать. Процедура
вычисления таких пределов носит название
- раскрытие неопределенности.
Приведем несколько примеров.
Пример 1. Вычислить предел
.
Решение. Подстановка предельного
значения х=2 в числитель и знаменатель
показывает, что они обращаются в ноль.
Для раскрытия неопределенности умножаем
числитель и знаменатель дроби на
выражение “ сопряженное числителю”,
то есть на сумму
,
получим
.
Пример 2.
Вычислить предел
Решение. Так как
,
для раскрытия неопределенности числитель
и знаменатель делим почленно на старшую
степень х, то есть на
,
получим
.
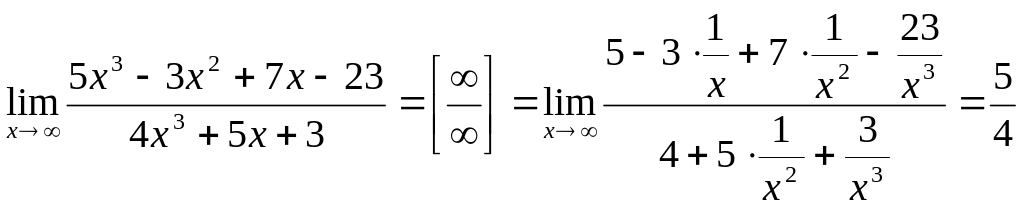Здесь воспользовались теоремами о пределах и тем, что функция обратная бесконечно большой является функцией бесконечно малой.
Пример 3. Вычислить предел
.
Решение. Поскольку числитель и знаменатель дроби обращается в ноль в т.х=3, то соответствующие многочлены можно разбить на множители и, таким образом , раскрыть неопределенность.
Замечание. Кроме рассмотренных
неопределенностей, могут встречаться
неопределенности вида
,
,
и др. К раскрытию каждой из них нужен
свой подход, например , раскрытие
неопределенности вида
требует применения , так называемого
второго замечательного предела.
4.6. Замечательные пределы
В ряде случаев раскрытию неопределенностей помогают два известных предела, которые в математике получили название «замечательные».
1). Первый замечательный предел
Пример. Вычислить предел
.
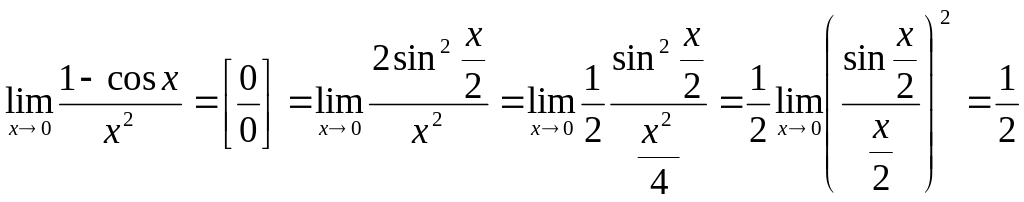
2). Второй замечательный предел
,
определяет число
Замечание 1. Логарифм с основанием
называется натуральным и обозначается
.
Замечание 2. Легко видеть, что второй
замечательный предел используется при
раскрытии неопределенностей вида
.
Замечание 3 Заменой переменной второй замечательный предел можно привести к одному из следующих видов:
,
,
.
Пример. Вычислить предел
Легко
вычислить
,
откуда видно , что исходный предел
представляет собой неопределенность
вида [
]
и раскрывается эта неопределенность с
помощью второго замечательного предела:
.
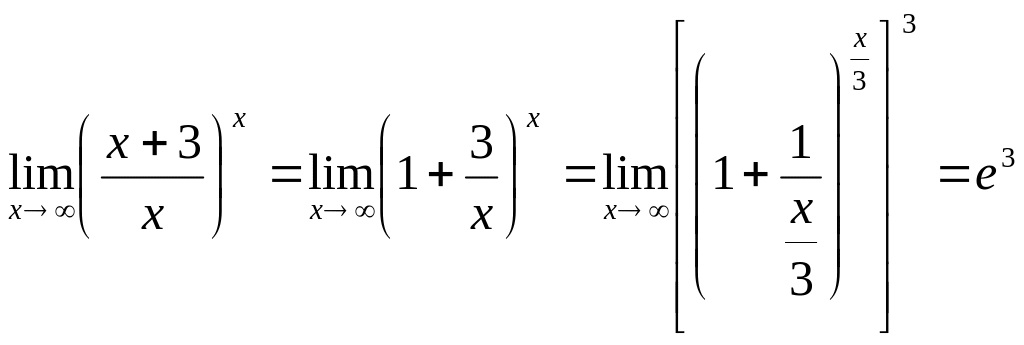5. Производная и дифференциал.
5.1. Определение производной функции
Рассмотрим функцию
,
определенную в некоторой окрестности
т.
.
Дадим аргументу
в точке
приращение
,
тогда функция
получит соответствующее приращение
.
Отношение
выражает относительное (среднее)
изменение функции
на
промежутке
,
а предел этого отношения, при
,
выражает скорость изменения функции
в т.
,
обозначается
или
,
и называется производной функции
в т.
.
Итак, по определению, производная
функции
по аргументу х есть
.
Например, если функция
выражает объем произведенной продукции
ко времени t , то
- определяет количество продукции
произведенной за время
.
Отношение
- выразит среднюю производительность
труда (скорость производства продукции
за время
),
а производная
- производительность труда в момент
времени
.
Геометрически, производная функции
в точке
равна тангенсу угла наклона
касательной прямой к графику этой
функции в точке с абсциссой
,
т.е.
-
угловой коэффициент касательной.
Уравнение этой касательной имеет вид:
.
Пример 1. Объем выпускаемой продукции
в течение дня задается функцией времени
,
.
Найти производительность труда в момент
времени t=4..
Решение. Производительность труда
определяется как производная от объема.
Тогда, с учетом того, что
,
получим
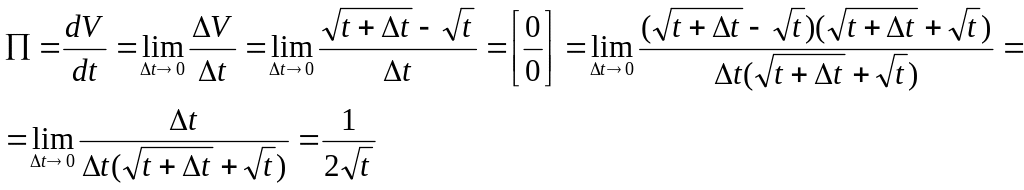
При
,
.
Пример 2. Написать уравнение
касательной к графику функции
в точке с абсциссой
.
Решение. Для того чтобы написать
уравнение касательной, вычисляем
и производную функции
.
Тогда
,
и уравнение касательной имеет вид
,
или, после преобразования,
.
Замечание. Способом, приведенным в этих примерах, (по определению), можно найти производную любой функции. Однако проделывать каждый раз эти рутинные вычисления предела, весьма утомительно. Далее мы познакомимся с правилами, которые позволяют избежать этих громоздких процедур. Эти правила дают возможность вычислять производные суммы, разности, произведения и других комбинаций функций, используя таблицу производных основных элементарных функций.