
- •Ю.В.Захаров Математическое моделирование
- •Введение
- •1. Основные сведения из теории вероятностей и
- •1.1. Случайные величины. Выборка
- •1.2. Законы распределения случайных величин
- •Экспоненциальный закон распределения
- •Hормальный закон распределения (hзр)
- •1.3. Числовые характеристики случайных величин Характеристики положения
- •Характеристики рассеяния
- •1.4. Статистическая проверка гипотез
- •Гипотеза о равенстве дисперсий
- •Гипотеза об однородности дисперсий
- •Гипотеза о равенстве средних
- •Гипотеза о законе распределения случайной величины
- •1.5. Ошибки измерения физических величин и методы
- •Случайные, систематические и грубые ошибки
- •Методы исключения резко выделяющихся результатов эксперимента
- •Табличные значения критерия Романовского
- •2. Выбор наиболее существенных факторов объекта
- •2.1. Метод экспертных оценок
- •Матрица рангов параметров
- •Сумма рангов и коэффициент весомости
- •Сводные результаты экспертизы
- •2.2. Метод начальных моментов
- •2.3. Дисперсионный анализ
- •Общая постановка и решение задачи да
- •Однофакторный да
- •3. Математическое моделирование в технологии
- •3.1. Методы математического моделирования
- •3.2. Пассивный эксперимент для мм
- •3.2.1. Регрессионный анализ.
- •Примеры.
- •3.2.2. Метод экспоненциального сглаживания
- •3.2.3. Корреляционный анализ.
- •3.2.4 Оценка адекватности мм.
- •3.3. Активный эксперимент для мм
- •3.3.1. Вид и алгоритм построения математической модели
- •3.3.2. Полный факторный эксперимент типа 2k.
- •Проверка воспроизводимости эксперимента
- •Вычисление коэффициентов модели.
- •Примеры вычислений коэффициентов пфэ 22
- •Проверка значимости коэффициентов модели.
- •Проверка адекватности модели.
- •Анализ и синтез тп по полученной модели.
- •Получение математической модели с учетом взаимодействий факторов.
- •3.3.3. Дробный факторный эксперимент.
- •В записи плана дфэ 2k-p p означает количество взаимодействий факторов приравненным независимым переменным. Дфэ 23-1 – половина пфэ 23, т.Е. Полуреплика от пфэ 23.
- •3.3.4. Математические модели второго порядка.
- •Контрольные вопросы
- •Заключение
- •Содержание введение
- •Заключение
- •Литература
3.3.4. Математические модели второго порядка.
Требуется получить ММ второго порядка вида
![]() .
(29)
.
(29)
Из теории интерполяции следует, что для нахождения коэффициентов модели число уровней каждой из независимых переменных в эксперименте должно быть на единицу больше полинома. Исходя из данного положения для получения модели (29) требуется число уровней факторов xi 3.
Применение планов ПФЭ 3k не рационально, поскольку это планирование характеризуется резким увеличением числа опытов в эксперименте.
Сократить число опытов можно, используя так называемые композиционные планы (КП), ядром которых является план ПФЭ 2k .
Преимущество этих планов состоит в том, что если гипотеза о линейности ММ не подтвердилась, то нет необходимости выполнять все эксперименты заново для получения модели более высокого порядка. В этом случае к проведенному эксперименту ПФЭ достаточно добавить некоторое число дополнительных опытов для получения плана эксперимента 2 порядка.
Получение композиционных планов второго порядка в случае неадекватности линейной модели производится в следующей последовательности:
1) проводится план ПФЭ 2k ;
2)
проводятся 2k
опытов в так называемых "звездных"
точках ( с координатами
![]() ),
где
),
где
![]() расстояние от центра плана до "звездной"
точки;
расстояние от центра плана до "звездной"
точки;
3) проводится n0 опытов в центре плана с координатами ( 0, 0, ... , 0 ). Тогда общее число опытов в КП при k факторах равно:
![]() .
.
Пример КП при k=2 в геометрической форме представлен на рис. 7.
X2
7
3
4
6
5
9
X1
1
2
8


![]()
![]()
![]()
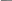

Рис. 7. Композиционный план при k = 2
а) точки 1,2,3,4 соответствуют опытам ПФЭ 22 ;
б) точки 5,6,7,8 с координатами ( ,0), ( ,0), (0, ), (0, ) соответствуют "звездным" точкам ;
в) точка 9 соответствует n0 числу опытов в центре плана .
Величина
"звездного" плеча
![]() и количество опытов в центре плана n0
определяются типом КП.
и количество опытов в центре плана n0
определяются типом КП.
Наибольшее распространение среди КП получили ортогональный центральный композиционный план (ОЦКП) и рототабельный центральный композиционный план (РЦКП).
ОЦКП
В ОЦКП число опытов в центре плана берется равным 1, а значение выбирается из условия ортогональности плана и оно равно:
k |
2 |
3 |
4 |
5 |
|
1 |
1,215 |
1,414 |
1,547 |
ОЦКП при К=3 содержит 15 опытов:
![]() ,
,
в то время как ПФЭ типа 33 содержит 27 опытов, т.е. имеется выигрыш по N.
![]() .
.
В качестве примера в табл.18 приведена матрица планирования ОЦКП при К=3.
Таблица 18
Матрица планирования ОЦКП при К=3.
N опыта |
Х1 |
Х2 |
Х3 |
|
|
|
Х1 Х2 |
Х1Х3 |
Х2Х3 |
Y |
1 |
-1 |
-1 |
-1 |
+0,27 |
+0,27 |
+0,27 |
+1 |
+1 |
+1 |
y1 |
2 |
+1 |
-1 |
-1 |
+0,27 |
+0,27 |
+0,27 |
-1 |
-1 |
+1 |
y2 |
3 |
-1 |
+1 |
-1 |
+0,27 |
+0,27 |
+0,27 |
-1 |
+1 |
-1 |
y3 |
4 |
+1 |
+1 |
-1 |
+0,27 |
+0,27 |
+0,27 |
+1 |
-1 |
-1 |
y4 |
5 |
-1 |
-1 |
+1 |
+0,27 |
+0,27 |
+0,27 |
+1 |
-1 |
-1 |
y5 |
6 |
+1 |
-1 |
+1 |
+0,27 |
+0,27 |
+0,27 |
-1 |
+1 |
-1 |
y6 |
7 |
-1 |
+1 |
+1 |
+0,27 |
+0,27 |
+0,27 |
-1 |
-1 |
+1 |
y7 |
8 |
+1 |
+1 |
+1 |
+0,27 |
+0,27 |
+0,27 |
+1 |
+1 |
+1 |
y8 |
9 |
-1,21 |
0 |
0 |
+0,74 |
-0,73 |
-0,73 |
0 |
0 |
0 |
y9 |
10 |
+1,21 |
0 |
0 |
+0,74 |
-0,73 |
-0,73 |
0 |
0 |
0 |
y10 |
11 |
0 |
-1,21 |
0 |
-0,73 |
+0,74 |
-0,73 |
0 |
0 |
0 |
y11 |
12 |
0 |
+1,21 |
0 |
-0,73 |
+0,74 |
-0,73 |
0 |
0 |
0 |
y12 |
13 |
0 |
0 |
-1,21 |
-0,73 |
-0,73 |
+0,74 |
0 |
0 |
0 |
y13 |
14 |
0 |
0 |
+1,21 |
-0,73 |
-0,73 |
+0,74 |
0 |
0 |
0 |
y14 |
15 |
0 |
0 |
0 |
-0,73 |
-0,73 |
-0,73 |
0 |
0 |
0 |
y15 |
где
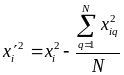 .
.
При
ОЦКП точность определения y
по модели
(29) в различных направлениях факторного
пространства на одинаковом расстоянии
от центра плана неодинакова,
т.е. при R
= const,
S2
{ y
}![]() const.
const.
Если основным требованием к плану является обеспечение одинаковой точности определения y во всех направлениях на одинаковом расстоянии R от центра плана, то применяется РЦКП.
РЦКП
Рототабельность- свойство обеспечения одинаковой дисперсии определения величины y во всех направлениях на одинаковом расстоянии от центра плана.
Условие рототабельности - при R = const, S2 { y } = const.
Для обеспечения условия рототабельности, величину выбирают из выражения:
![]() ,
,
а значения n0 определяются в зависимости от числа факторов. Для ПФЭ 2k имеем:
k |
2 |
3 |
4 |
5 |
6 |
7 |
n0 |
5 |
6 |
7 |
10 |
15 |
21 |
Общее
число опытов NРЦКП
:
![]() .
.
