Проверка адекватности модели.

Осуществляется по F-критерию Фишера.

1. Определяется остаточная дисперсия S²_ост. , характеризующая рассеяние экспериментальных данных относительно результатов, полученных по найденной ММ

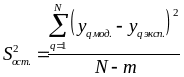, (25)

где y_{q мод.} - величина показателя качества для q-го опыта. Рассчитывается при подстановке в полученную модель вычисленных значений и значений для данного опыта;

y _{q эксп.}- экспериментально полученное значение у в q-ом опыте;

m - общее число значимых коэффициентов модели, включая и коэффициент b₀ .

2. Рассчитывается расчетное значение F_рас.

,

где S²_восп - дисперсия воспроизводимости эксперимента.

3. Находится:

при М дублированных строках матрицы;

при одной дублированной строке матрицы.

4. Сравниваются F_рас. и F_таб.:

если F_рас. < F_таб , то с вероятностью p=1- ММ считается адекватной;

при F_рас. F_таб - неадекватной.

При неадекватной модели необходимо:

1) дополнить описание ММ составляющими, характеризующими взаимодействие факторов;

2) переходить к квадратному уравнению;

3) переходить к более сложному уравнению.

Анализ и синтез тп по полученной модели.

Заключается в использовании физического смысла коэффициента b_i и его знака.

1. Абсолютная величина коэффициента b_i характеризует степень влияния i-го фактора на показатель качества y. Чем больше абсолютная величина b_i, тем большее влияние оказывает i-ый фактор на y.

2. Знак коэффициента характеризует направление изменения y при изменении i-го фактора. Если знак "+" , то изменение значений x_i и y происходит в одном направлении, если знак "-" , то изменение значений x_i и y происходит в противоположном направлении.

Получение математической модели с учетом взаимодействий факторов.

При проведении ПФЭ 2^k возможно получение ММ с учетом взаимодействий двух факторов, причем эта возможность реализуется без увеличения числа опытов.

Эта модель имеет вид:

. (26)

Для вычисления коэффициентов b_ij необходимо иметь матрицу планирования, в которой учтены парные взаимодействия. Эта матрица представлена в табл.14

Таблица 14

Матрица планирования ПФЭ 2³ с парными взаимодействиями

N опыта	x1	x2	x3	x1x2	x1x3	x2x3	yэксп.
1	-1	-1	-1	+1	+1	+1	y1
2	+1	-1	-1	-1	-1	+1	y2
3	-1	+1	-1	-1	+1	-1	y3
4	+1	+1	-1	+1	-1	-1	y4
5	-1	-1	+1	+1	-1	-1	y5
6	+1	-1	+1	-1	+1	-1	y6
7	-1	+1	+1	-1	-1	+1	y7
8	+1	+1	+1	+1	+1	+1	y8

Коэффициенты b_ij вычисляются по формуле

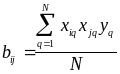. (27)

Отличие формулы (27) от (24) заключается в том, что здесь вместо значений x_iq берутся взаимодействия x_iq x_jq­ .Например из таблицы 14 имеем:

.

Матрица планирования, приведенная в таблице 14, обладает свойствами ортогональности, симметричности, нормировки и рототабельности.

Статистический анализ модели (26) ничем не отличается от статистического анализа модели (22), кроме того, что здесь надо учитывать коэффициенты b_ij и значения x_iq x_jq .

При проведении ПФЭ 2^k возможно получение моделей с учетом 3-х,

4-х и т.д. взаимодействий. Учет по аналогии с вышесказанным.

Пример. Построить математическую модель вида:

y=b₀+ b₁ x₁+ b₂ x₂+ b₃ x₃+ b₄ x₄+ b₁₂x₁x₂+ b₁₃x₁x₃+ b₁₄x₁x₄+ b₂₃x₂x₃+ b₂₄x₂x₄+ b₃₄x₃x₄.

В табл.15 приведена матрица планирования ПФЭ 2⁴ с парными взаимодействиями 4 факторов и экспериментальные значения показателя качества (y_эксп). Опыты 17-20 выполнены в центре плана эксперимента для вычисления s²_вос.

Таблица 15

№ опыта	x1	x2	x3	x4	x1x2	x1x3	x1x4	x2x3	x2x4	x3x4	yэксп
1	-1	-1	-1	-1	+1	+1	+1	+1	+1	+1	0,87
2	+1	-1	-1	-1	-1	-1	-1	+1	+1	+1	0,84
3	-1	+1	-1	-1	-1	+1	+1	-1	-1	+1	0,98
4	+1	+1	-1	-1	+1	-1	-1	-1	-1	+1	0,9
5	-1	-1	+1	-1	+1	-1	+1	-1	+1	-1	1
6	+1	-1	+1	-1	-1	+1	-1	-1	+1	-1	0,97
7	-1	+1	+1	-1	-1	-1	+1	+1	-1	-1	1,09
8	+1	+1	+1	-1	+1	+1	-1	+1	-1	-1	1,07
9	-1	-1	-1	+1	+1	+1	-1	+1	-1	-1	0,87
10	+1	-1	-1	+1	-1	-1	+1	+1	-1	-1	0,83
11	-1	+1	-1	+1	-1	+1	-1	-1	+1	-1	0,93
12	+1	+1	-1	+1	+1	-1	+1	-1	+1	-1	0,78
13	-1	-1	+1	+1	+1	-1	-1	-1	-1	+1	0,87
14	+1	-1	+1	+1	-1	+1	+1	-1	-1	+1	0,75
15	-1	+1	+1	+1	-1	-1	-1	+1	+1	+1	1,07
16	+1	+1	+1	+1	+1	+1	+1	+1	+1	+1	1
17	0	0	0	0	0	0	0	0	0	0	0,95
18	0	0	0	0	0	0	0	0	0	0	0,92
19	0	0	0	0	0	0	0	0	0	0	0,9
20	0	0	0	0	0	0	0	0	0	0	0,91

Вычисление коэффициентов модели

Коэффициенты модели вычисляются по формулам (23), (24) и (27). Расчеты производились с точностью до 3 знаков после запятой:

b₀=(0,87+0,84+0,98+0,9+1+0,97+1,09+1,07+0,87+0,83+0,93+0,78+0,87+ 0,87+0,75+1,07+1)/16=0,927;

b₁=(-0,87+0,84-0,98+0,9-1+0,97-1,09+1,07-0,87+0,83-0,93+0,78-0,87+0,75 -1,07+1)/16=-0,034;

b₂=(-0,87-0,84+0,98+0,9-1-0,97+1,09+1,07-0,87-0,83+0,93+0,78-0,87-0,75 +1,07+1)/16=0,051;

b₃=(-0,87-0,84-0,98-0,9+1+0,97+1,09+1,07-0,87-0,83-0,93-0,78+0,87+0,75 +1,07+1)/16=0,051;

b₄=(-0,87-0,84-0,98-0,9-1-0,97-1,09-1,07+0,87+0,83+0,93+0,78+0,87+0,75 +1,07+1)/16 = -0,039;

b₁₂=(0,87-0,84-0,98+0,9+1-0,97-1,09+1,07+0,87-0,83-0,93+0,78+0,87-0,75-1,07+1)/16=-0,006;

b₁₃=(0,87-0,84+0,98-0,9-1+0,97-1,09+1,07+0,87-0,83+0,93-0,78-0,87+0,75-1,07+1)/16=0,004;

b₁₄=(0,87-0,84+0,98-0,9+1-0,97+1,09-1,07-0,87+0,83-0,93+0,78-0,87+0,75-1,07+1)/16=-0,014;

b₂₃=(0,87+0,84-0,98-0,9+1-0,97+1,09+1,07+0,87+0,83-0,93-0,78-0,87-0,75+1,07+1)/16=0,029;

b₂₄=(0,87+0,84-0,98-0,9+1+0,97-1,09-1,07-0,87-0,83-0,93+0,78-0,87-0,75+ 1,07+1)/16=0,006;

b₃₄=(0,87+0,84+0,98+0,9-1-0,97-1,09-1,07-0,87-0,83-0,93-0,78+0,87+0,75+ 1,07+1)/16=-0,017.

Проверка значимости коэффициентов модели

Проверка значимости коэффициентов модели осуществляется по t-критерию Стьюдента. Для этого предварительно вычислим дисперсию воспроизводимости S²_вос:

,

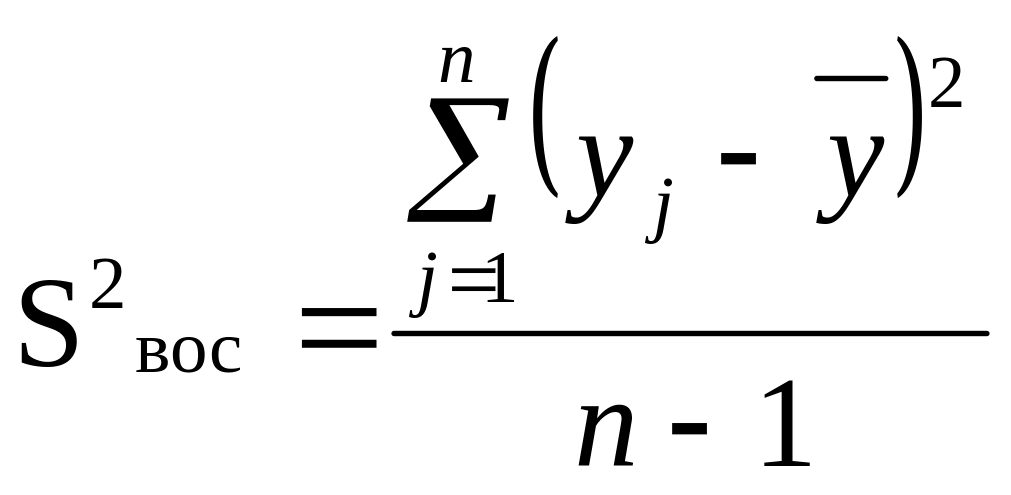где - значения показателя качества в центре плана эксперимента;

- среднее значение показателя качества из опытов;

- число опытов в центре плана эксперимента ( =4).

Имеем: =(0,95+0,92+0,9+0,91)/4=0,92;

=[(0,95-0,92)²+(0,92-0,92)² +(0,9-0,92) ² +(0,91-0,92) ²]/3=0,00047.

1. Вычислим t_расч каждого коэффициента модели по формуле:

, где = =0,0217; =16.

Для коэффициента b₀ имеем . Аналогичным образом найдем для коэффициентов b_1,b_2,….,b₃₄. Получим t₁=6,1; t₂=9,4; t₃=9,4; t₄=7,2; t₁₂=1,1; t₁₃=0,7; t₁₄=2,6; t₂₃=5,4; t₂₄=1,1; t₃₄=2,9.

2. Находим табличное значение t_табл =f(; ₁= ). При =0,1 и =4: t_табл=2,35.

3. Сравниваем t_расч и t_табл. С вероятностью 0,9 следует, что коэффициенты

b_0,b_1,b_2,b_3,b_4,b_14,b_23,b₃₄ – значимые, т.к. для них выполняется условие t_расч>t_табл .

Исключив незначимые коэффициенты, получим математическую модель в виде:

y = 0.927- 0.034 x₁+ 0.051x₂+ 0.051 x₃- 0.039 x₄- 0.014 x₁x₄+ 0.029 x₂x₃-0.016b₃₄x₃x₄ . (28)

Проверка адекватности полученной модели

Осуществляется по F-критерию Фишера.

1. Определим остаточную дисперсию по формуле (25), где =16; m=8. Предварительно вычислим значения у_мод по выражению (28), подставив вместо х₁, х₂,…, х₃ х₄ значения -1 или +1 из табл.15. Для у_1мод имеем:

Аналогичным образом получим: 0,864; 0,944 ; 0,884; 0,969; 0,949; 1,129; 1,084; 0,869; 0,779; 0,939; 0,824; 0,874; 0,799; 1,059; 0,959.

Тогда [(0.897-0.87)²+(0.864-0.84)²+(0.944-0.98)²+(0.8840.9)²+(0.968-1)²+(0.949-0.97)²+(1.129-1.09)²+(1.084-1.07)²+(0.869-0.87)²+(0.779-0.83)²+(0.939-0.93)²+(0.824-0.76)²+(0.874-0.87)²+(0.799-0.75)²+(1.059-1.07)²+(0.959-1)²]/8=0.00298.

2. Вычислим .

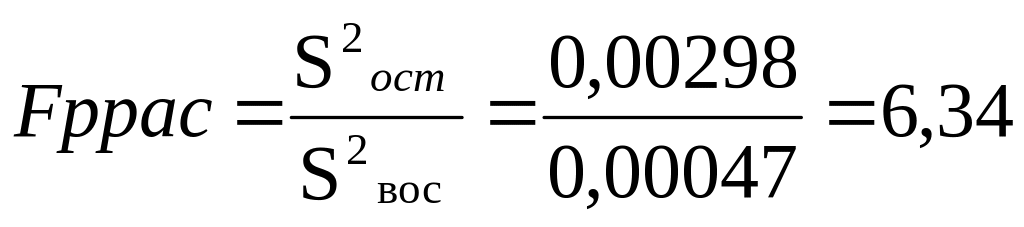3. Находим f(₁=N-m, ₂=n-1) при =0,05: .

4. Сравним 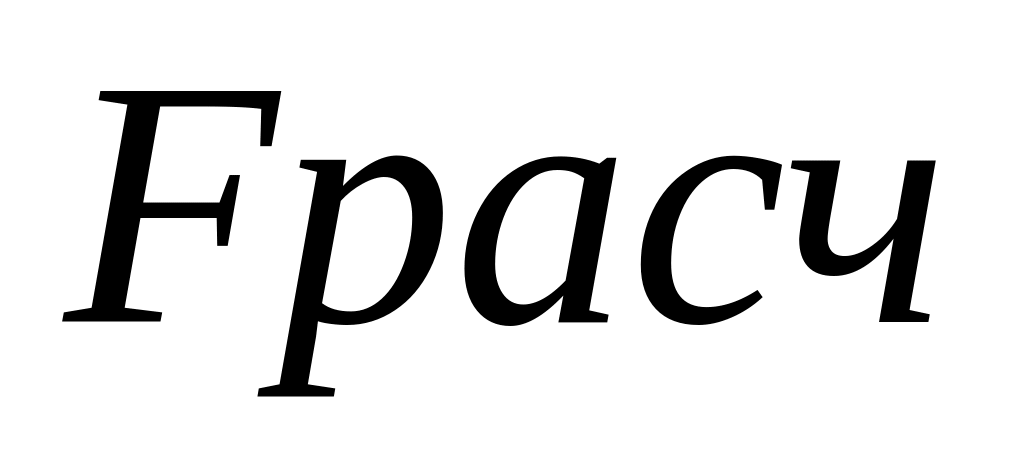и . Так как 6,34<8,84, то с вероятностью 0,95 математическая модель (28) считается адекватной экспериментальным данным.

Таким образом, искомая математическая модель имеет вид выражения (28).