3.2. Пассивный эксперимент для мм

3.2.1. Регрессионный анализ.

Пусть имеется только один фактор, определяющий y.

х - не случайная величина (СВ);

y - СВ, принимающая значения в некотором интервале.

y = f(х).

Эта зависимость ищется в виде y = β₀ + β₁ x .

Реально модель имеет вид (8) , которая показывает как в среднем изменяется величина y при изменении величины х в заданном диапазоне. Здесь b₀ и b₁ являются оценками теоретических коэффициентов β₀ и β₁.

Уравнение (8) - уравнение регрессии y по х. Графическое изображение (8)-кривая регрессии.

Коэффициенты уравнения b₀ и b₁ находятся по экспериментальным данным методом наименьших квадратов (МНК). МНК позволяет получить несмещенные, состоятельные и эффективные оценки.

Имеем экспериментальные данные:

Х	х1	х2	...........	хi	...........	хn
Y	у1	у2	...........	уi	...........	уn

Суть МНК: минимизируется сумма квадратов отклонений измеренных значений y_i от значений вычисленных по уравнению регрессии (рис. 2).

y,

у_n

у₃

у₂

у₁

x₁ x₂ x₃ x_n x

Рис. 2. Линейное уравнение регрессии

min

МНК: ;

. (9)

Выполнение условия (9) обеспечивается так:

по коэффициентам уравнения (8) b₀ и b₁ определяются частные производные функции U и приравниваются к нулю. В результате образуется система нормальных уравнений, число которых равно числу неизвестных коэффициентов.

Для (9) имеем:

1) ;

2)

Получили систему

Решив ее, найдем b₀ и b₁.

На основе регрессионного анализа можно получить уравнение регрессии вида

.

В этом случае система нормальных уравнений имеет вид:

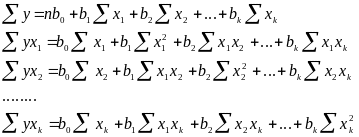
Решается на ЭВМ с использованием стандартной программы.

Мы рассмотрели построение линейных относительно х уравнений регрессии. Но на практике приходится иметь дело и с нелинейными зависимостями y=f(x_н,а,b). При определении коэффициентов таких функций иногда удается путем замены переменных привести ее к виду =b₀+b₁x, т.е. линейному виду. Такая процедура называется выравниванием эмпирической формулы. Далее b₀ и b₁ находятся МНК, а затем производится их пересчет к а и b.

Примеры.

1. Степенная функция y = a x_н^b .Применяется логарифмическое преобразование:

lg y = lg a + b lg x_н . Замена переменных:

lg y = ; lg x_н = x. Получим = b₀ + b₁x, где b₀ = lg a, b₁ = b.

2. Показательная функция y = . Логарифмическое преобразование:

lg y = lg a + b x_н lg e . Замена переменных:

lg y = ; x_н = x. Получим = b₀ + b₁x, где b₀ = lg a, b₁ = b lg е.

3. Функция вида . Преобразование:

Замена переменных:

Получим = b₀ + b₁x, где b₀ = b, b₁ = a.

Более подробно о регрессионном анализе см. в [9]