4. Лабораторная работа № 3 исследование синтеза сигналов по фурье

Цель работы. Изучить возможности синтеза сигналов с помощью ряда Фурье по ортогональной системе тригонометрических функций. Синтезировать периодические сигналы различной формы и исследовать влияние числа ортогональных составляющих на погрешность аппроксимации.

4.1. Разложение сигналов в обобщенный ряд фурье

4.1.1. Спектры простейших периодических функций

Если функция четная (симметричная относительно оси ординат), т.е. , то в этом случае

; (4.1)

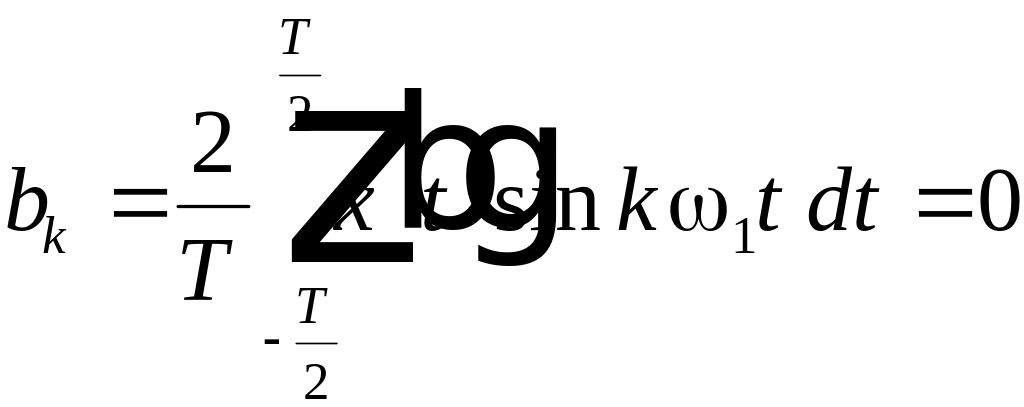. (4.2)

Разложение функции будет следующим

. (4.3)

Аналогично для нечетной функции можно найти, что

. (4.4)

На рис. 4.1 показана последовательность прямоугольных импульсов которую можно рассматривать как четную функцию.

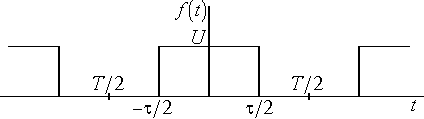
Рис. 4.1. Последовательность прямоугольных импульсов

По формуле (4.1) находим амплитуду -й гармоники:

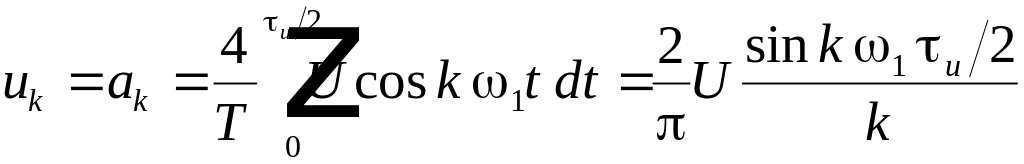. (4.5)

Постоянная составляющая будет равна

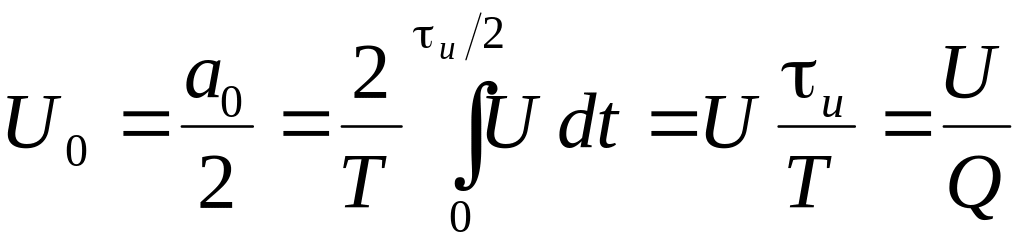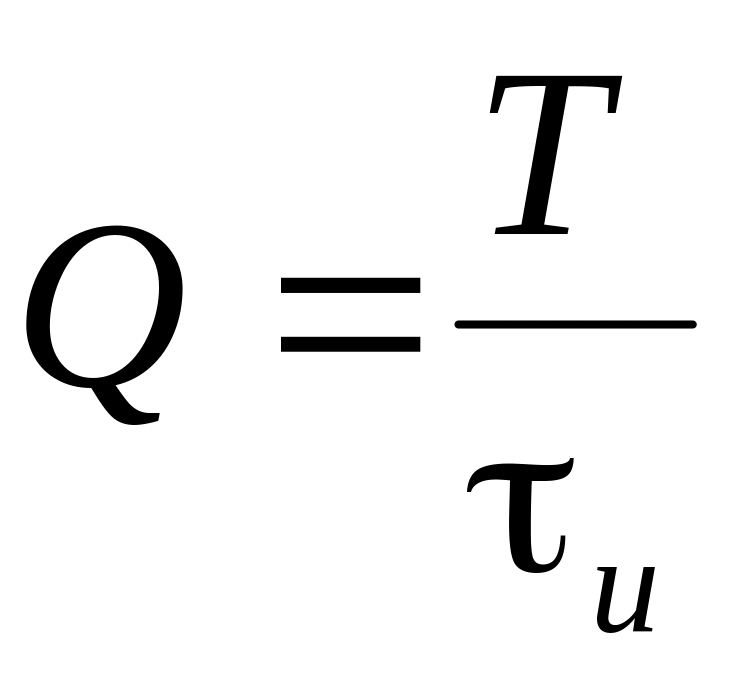; . (4.6)

где – скважность импульсов. Разложение функции запишется в виде:

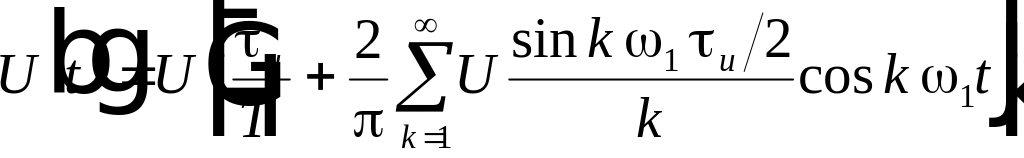. (4.7)

Графически амплитудный и фазовый спектры прямоугольных импульсов показаны на рис. 4.2.

Расстояния между отдельными спектральными составляющими обратно пропорциональны периоду следования импульсов - , а положение нулей кратно .

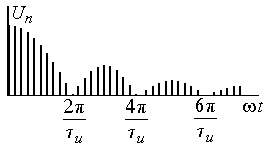
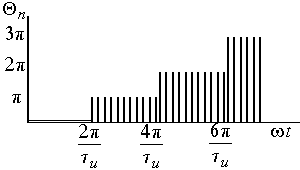
а) б)

Рис. 4.2. Амплитудный и фазовый спектры прямоугольных импульсов

Можно показать, что для импульсов, представленных на рис. 4.3, разложения в ряд Фуре будут иметь следующий вид:

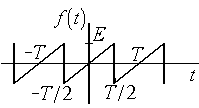
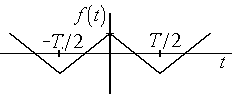
а) б)

Рис. 4.3. Пилообразное колебание и треугольные импульсы

для периодического пилообразного колебания (рис 4.3,а);

; (4.8)

для периодической последовательности треугольных импульсов (рис.4.3,б):

. (4.9)

4.1.2. Мощность и действующее значение периодического сигнала

Пусть несинусоидальный периодический ток течет через активное сопротивление . Средняя за период мощность будет равна

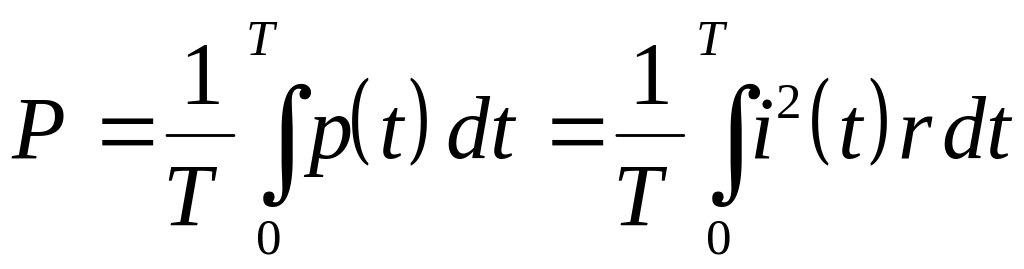. (4.10)

здесь мгновенная мощность. Представим функцию в виде ряда Фурье (4.6), тогда

.

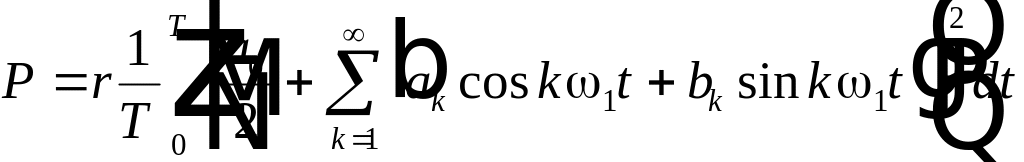Возводя в квадрат и интегрируя каждое из слагаемых можно убедиться, что только интегралы вида:

,

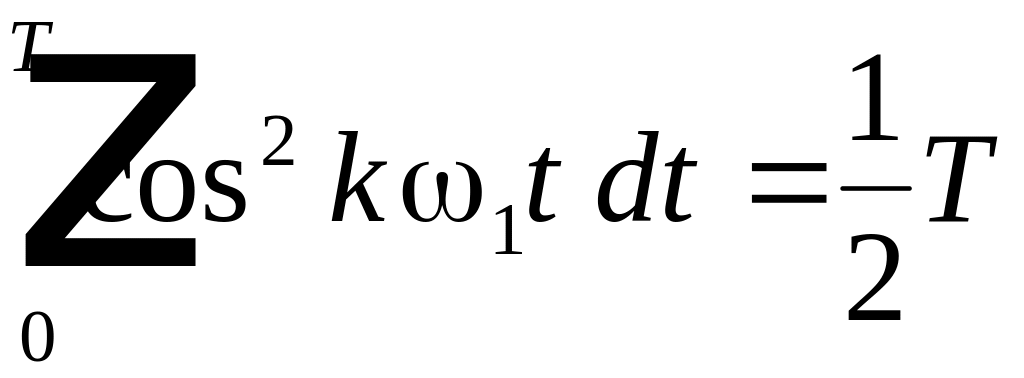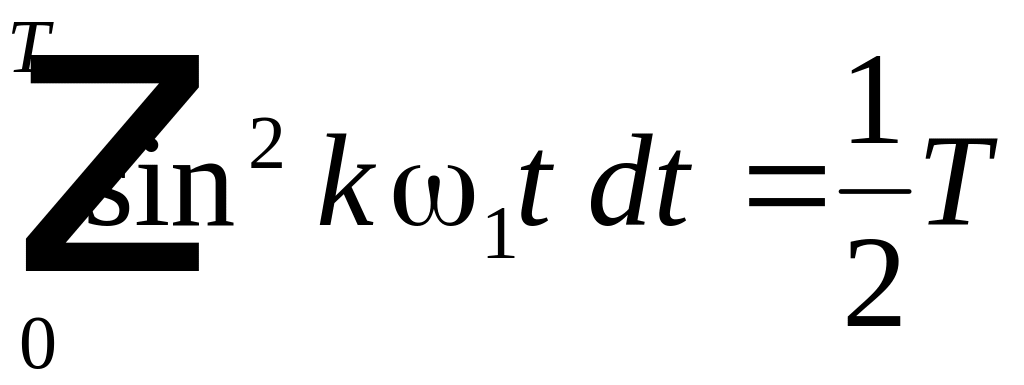
имеют значения, не равные 0. Все остальные интегралы равны нулю Поэтому после интегрирования получим

,

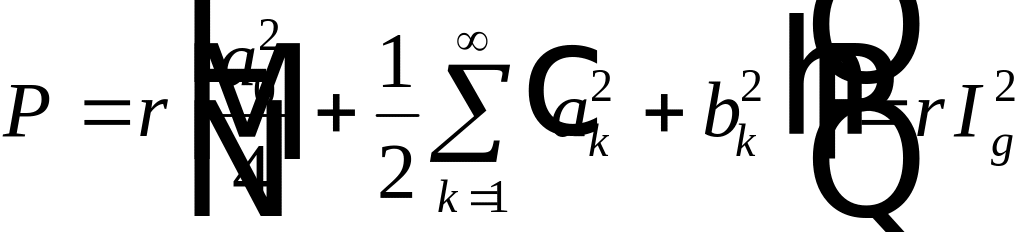где

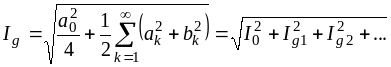. (4.11)

; ; . (4.12)

Величины , , , , ... называют действующими значениями тока. Аналогично вычисляются и действующие значения напряжения. Если сопротивление Ом, то мощность равна

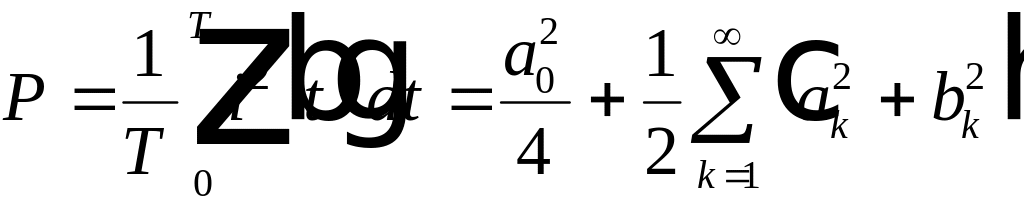. (4.13)

Последнее выражение справедливо для любой периодической функции, т.е.

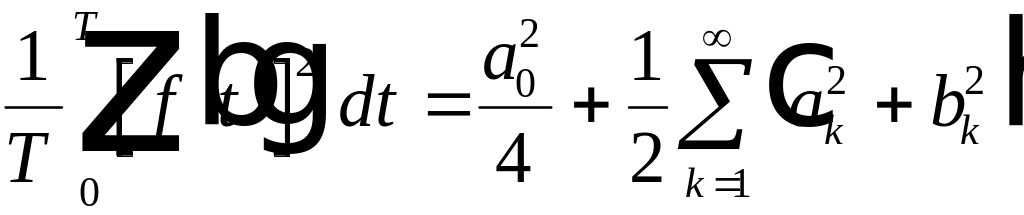. (4.14)

В таком виде последнее соотношение носит название равенства Парсеваля.

4.1.3. Среднеквадратическая погрешность аппроксимации

Представим приближенно функцию разложением в усеченный ряд по ортонормированным базисным функциям (см. п. 2.1)

(4.15)

и определим коэффициенты так, чтобы минимизировать среднеквадратическую погрешность:

.

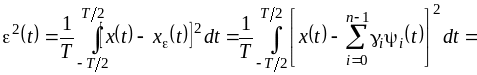
С учетом (2.4) можно записать

. (4.16)

Погрешность принимает минимальное значение, если , т.е. если коэффициенты разложения в усеченном представлении (4.15) являются коэффициентами обобщенного ряда Фурье. Исходя из (4.16) можно записать

или

. (4.17)

Неравенство (4.17) называют неравенством Бесселя. С ростом величина среднеквадратической погрешности уменьшается. Если при среднеквадратическая погрешность стремится к нулю, то систему базисных функций называют полной. Эта система функций является также замкнутой, т.к. для любой функции неравенство (4.17) переходит при в равенство.

Точность аппроксимации периодических сигналов зависит от числа членов ряда при конечном числе членов ряда. Относительную среднеквадратическую погрешность аппроксимации периодической функции конечным числом членов ряда Фурье можно определить по формуле :

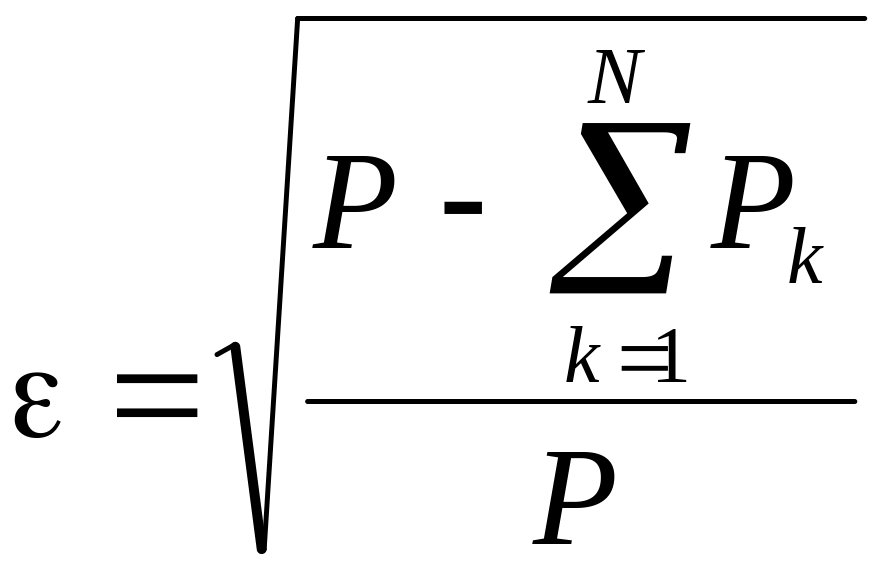. (4.18)

где — средняя мощность сигнала; — средняя мощность -й ортогональной составляющей сигнала.

Экспериментальное значение погрешности аппроксимации может быть найдено следующим образом. Пусть имеется экспериментально полученных точек сигнала. Известен также теоретический вид зависимости. Тогда погрешность аппроксимации может быть вычислена следующим образом

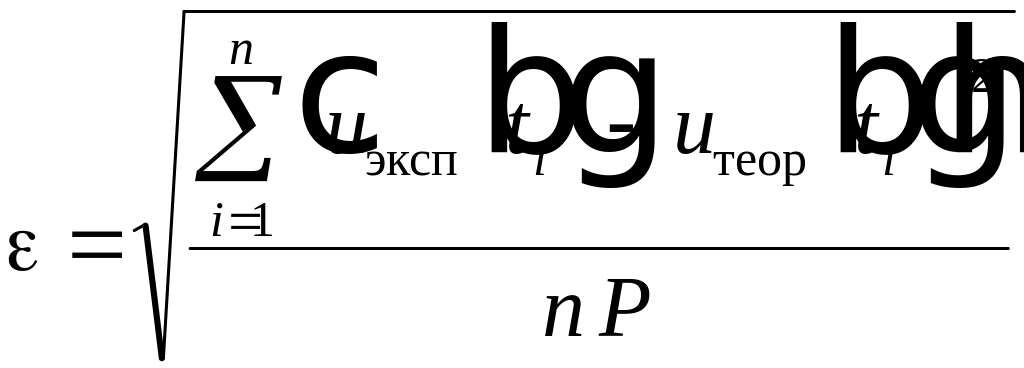, (4.19)

где - теоретическое значение отсчета сигнала в момент времени .