3. Относительный покой жидкости

Как уже указывалось, при рассмотре­нии относительного покоя жидкости под на­пряжением массовой силы в уравнени­ях (2) следует понимать равнодействую­щую напряжений силы тяжести и силы инерции переносного движения.

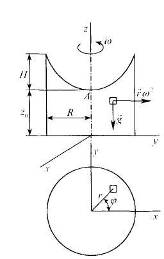
Рассмотрим задачу о вращении с посто­янной угловой скоростью ω сосуда с жидко­стью вокруг вертикальной оси Оz (рис. 6). На элемент жидкости массой ∆m действует сила тяжести и центробежная сила, напря­жения которых равны

,

где ř ~ вектор, направленный по кратчайшему расстоянию от оси вращения к рассматриваемому элементу. Проекции этих напряжений на выбранные оси координат O.xyz равны

Подставив эти значения в уравнения (4) и (5), имеем

Интегрируя эти соотношения, получим

(17)

(18)

Рис.6.

Уравнение (17) дает закон распределения давления в жидкости, а со­отношение (18) представляет собой уравнение семейства изобар, представ­ляющих собой параболоиды вращения. Для определения константы С в уравнении (17) и уравнении свободной поверхности (18) рассмотрим точку А пересечения свободной поверхности с осью 0z. Точка А имеет координаты (0, 0, z0), а давление в этой точке рав­но р0. Тогда из уравнений (17) и (18) имеем С = р0 +gz0, С1=gz0 и

Для определения высоты Н параболоида положим в уравнении (20) r = R , где R - радиус сосуда.

Тогда

.

Из уравнения (20) имеем

,

где z₁ - координата точек пересечения вертикальных прямых r₁=const со свободной поверхностью. Подставив это соотношение в уравнение (19), получим

(21)

Таким образом, если отсчитывать координату z от свободной поверхно­сти, то распределение давления по вертикали во вращающемся сосуде будет таким же, как и в покоящейся жидкости. Это объясняется тем, что проекция силы инерции на ось 0z равна нулю.

Полученный результат следует также непосредственно из форму­лы (3). Действительно, в рассматриваемом случае

,

откуда после интегрирования сразу получается формула (21).

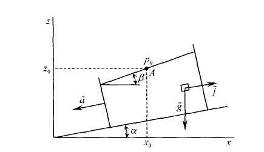
Рассмотрим теперь движение сосуда с жидкостью по наклонной плоско­сти с постоянным ускорением ā (рис. 7).

Рис. 7.

Проекции напряжения массовых сил на координатные оси равны где а - угол наклона плоскости к горизонту, . Подставив эти значения в уравнения (4) и (5), имеем

Из соотношения (23), представляющего собой уравнение семейства изобар, получим

(24)

то есть изобары представляют собой плоскости, наклоненные иод углом β к горизонту.

Интегрируя уравнение (22), получим закон распределения давления

Для определения константы интегрирования С положим, что в точ­ке H(x_o,0,z₀) р=р₀. Тогда

(25)

Рассмотрим некоторые частные случаи.

а) Спуск по вертикальной стене, то есть а =π/2. Из формулы (24) сле­дует, что β=0, z=const. Изобары представляют собой горизонтальные плос­кости. Из формулы (25) имеем

При свободном падении j = g и р = р₀, то есть давление во всех точках жидкости одинаково. Единственной действующей на жидкость силой будет поверхностное натяжение, под действием которого жидкость стягивается в шар.

б) Скольжение по плоскости без трения. В этом случае j=gsinα и из формулы (24) получим, что tgβ=tgα, то есть эквипотенциали параллель­ны плоскости скольжения. Из формулы (25) имеем