1. Основные понятия

Опр. : Случайной величиной (СВ) наз. переменная, значение которой зависит от случая. СВ бывает: 1) дискретная; 2) непрерывная.

Опр.: СВД – это величины, принимающие только отделенные друг от друга значения.

Опр. : СВН – это СВ, возможные значения которых непрерывно заполняют некоторый промежуток.

СВ ς всегда связана с некоторой функцией f(x) плотности распределения вероятностей СВ. Из теоремы о сложении вероятностей имеем

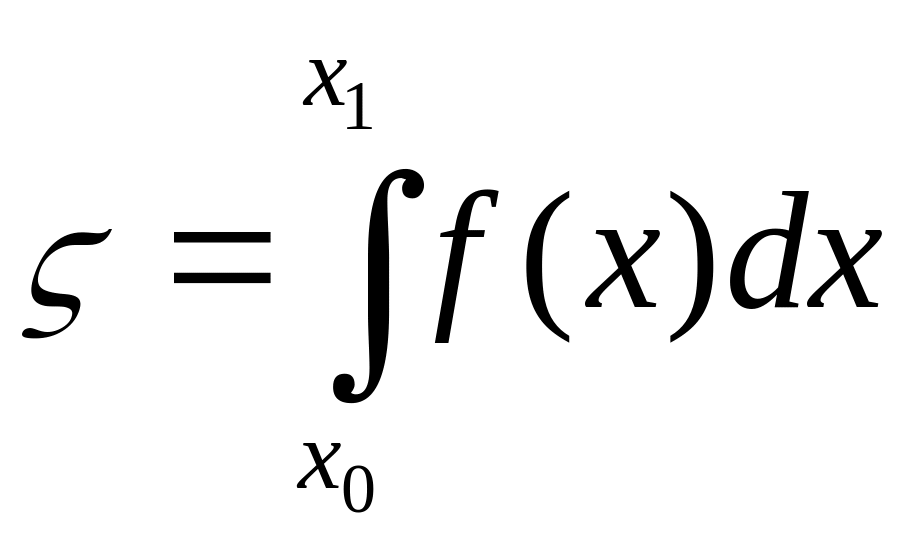- вероятность попадания ς в интервал [x₀, x₁]. Т.к. СВ всегда принимает какое-либо значение, то вероятность того, что наверняка попадем в интервал -[∞, +∞] есть . Это условие нормировки.

Опр.: Функция распределения СВ в точке x: F(x) наз. величина

.

Для СВД также можно определить функцию плотности и функцию распределения. Наиболее полная характеристика СВ дается ее функцией распределения, которая указывает на то, какие значения может принимать СВ и с какими вероятностями.

Для обработки СВ в теории вероятности вводятся количественные характеристики:

1. математическое ожидание (среднее значение) М(x).;

2. дисперсия ;

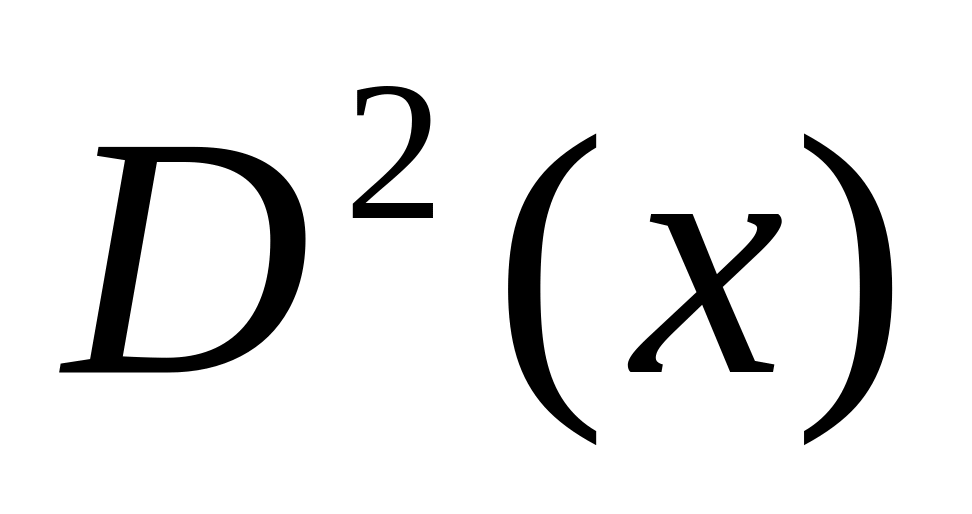3. моменты различных порядков.

Дадим определения этим понятиям.

Пусть x₁ , x₂, x₃, , , x_n – возможные значения СВД. P₁ , P₂, P₃, , , P_n – соответствующие им вероятности. Тогда наз. математическим ожиданием СВ ς, μ – результат суммирования. Если вероятности всех x_i равны, то , где n – число значений x, тогда имеем .

Опр.: Для СВН: Если СВ ς непрерывна и f(x) – ее плотность распределения, то математическим ожиданием (средним значением) для ς наз. интеграл

, (1)

где μ – результат вычисления интеграла.

Опр.: Дисперсия (разброс СВ относительно среднего значения) характеризуется:

, (2)

где - результат вычисления интеграла; - среднее значение квадрата СВ:

.

Опр.: Отклонением стандартным или среднеквадратичным наз. .

Для сравнения рассеяния различных случайных величин определяют относительное стандартное отклонения .

Примеры функции плотности распределения – прямоугольное равномерное распределение, нормальное распределение (распределение Гаусса).

2. Понятие о выборке

Формулировка задача. Предположим: требуется измерить величину l₀. Выполнив ряд измерений, имеем набор чисел: x₁, x₂, x₃, … . Какое значение из них следует принять за значение l₀?

Методика. Из-за влияния ошибок измерения имеем результат измерения СВ – ς, которая имеет некоторую функцию распределения. Если бы эта функция была известна, то можно условиться: принять за l₀ одну из характеристик СВ, например, ее среднее значение. Однако на практике возникают ситуации.

Функция распределения неизвестна. Поэтому предполагается следующее. Имеет место нормальное распределение, но параметры распределения μ, σ неизвестны. Если возможно производить множество измерений, тогда можно определить функцию плотности и среднее значение.

Т.к. число опытов n конечно для ς, то имеем наблюдения: x₁, x₂, x₃, … x_n. Эти x_i наз. случайной выборкой объема n из возможных значений ς.

Из математической статистики имеем: по результатам каждой выборки x₁, x₂, x₃, … x_n можно определить величину среднего значения μ и дисперсию σ распределения ς.

Тогда, пусть

- выборочное среднее значение СВ ς. (1)

Выборочная дисперсия СВ:

, (2)

среднее значение СВ- , (3)

дисперсия СВ . (4)

При больших значениях n СВ мало отличается от μ

На этом основывается обстоятельство, что выборочное среднее значение СВ по (1), принимается в качестве оценки значения μ.

Кроме того,

,

.

Т. е. стандартное отклонение ( ) при больших объемах выборки может быть как угодно малым.

Таким образом, при больших n СВ S² будет как угодно мало отличаться от среднего значения σ². С учетом сказанного S² [по (2)] берется в качестве оценки значения σ².

В данном случае для оценки стандартного отклонения величины , которое обозначим имеем:

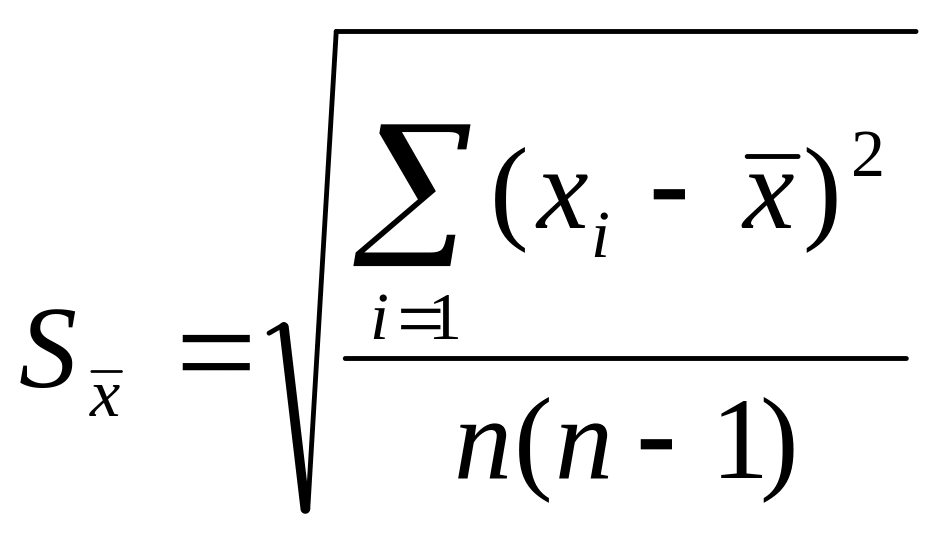. . (5)

Выводы. 1) по формуле (5) вычисляем оценку среднего значения μ (она наз. точечной оценкой).

2) выборочное значение – стандартное отклонение этой оценки – позволяет судить о том, как сильно величина может отличаться от среднего значения μ.

Итак, на данном этапе мы нашли величину μ функции распределения величины .Однако, сама функция распределения неизвестна.

Для ее построения используем формулы (1), (5), которые дают доверительный интервал

. (6)

Здесь k_α – положительное число, зависящее от параметра α, где α – коэффициент доверия - вероятность того, что μ заключено внутри интервала (6).

Доверительный интервал можно построить, если известны: 1) функция плотности f( ); 2) дисперсия СВ .

Действительно, вероятность

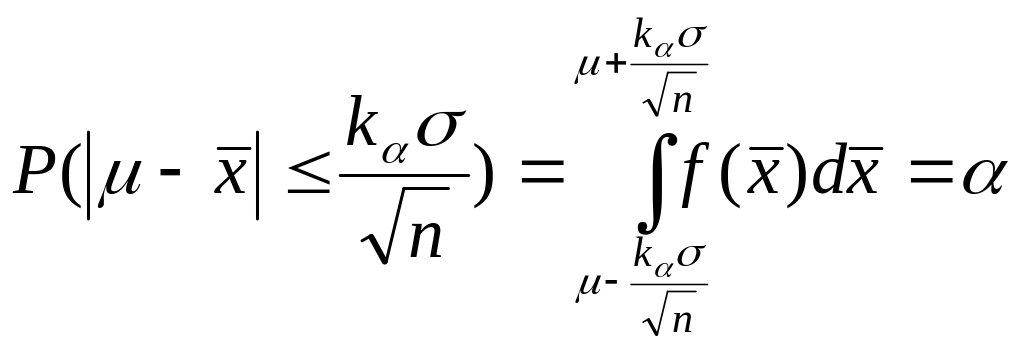. (7)

Из (7) для заданного α можно определить . Кроме того, можем записать

. (8)

И для коэффициента доверия α имеем интервал для μ

. (9)

Здесь не зависит от конкретного значения μ. Для его определения необходимо задать закон распределения .

1. В случае , если известно, что ς и распределены по нормальному закону и дисперсия не задана, то интервал, в котором может находиться с заданной достоверностью α, имеет вид

. (10)

Здесь вычисляются по результатам измерений, - коэффициент Стьюдента по заданной надежности α и числу измерений n находится по таблицам.

2. Если функция плотности для СВ неизвестна, а дисперсия задана, то используя неравентсво Чебышева, можно построить интервал для μ:

. (11)

Это означает, что вероятность того, что μ лежит внутри интервала (11), не меньше α, причем γ_α определяется

.

Заметим, что в гидродинамических процессах учитывают ошибки: 1) случайные; 2) систематические. Первую группу составляют ситуации их учета: 1) указывается функция плотности; 2) когда систематические ошибки =0, то указывается интервал, в котором с установленной вероятоностью находится случайная ошибка; 3) указывается оценка стандартного отклонения.

Функцию плотности f(x) удается указать лишь в немногих случаях, когда она известна, иногда можно определить доверительный интервал. В остальных случаях вычисляется выборочное стандартное отклонение.