1.3. Математическая обработка результатов опыта

Завершая эксперимент необходимо выполнить расчеты, провести анализ результатов, сделать выводы.

При прямых измерениях получают выборочное среднее

. (1)

Оценку стандартного отклонения случайных ошибок имеем в виде:

. (2)

Далее определяем различные системные ошибки

, (3)

где соответственно приведены ошибки: прибора (определяется по паспорту), округления ( ), субъективных измерений.

Если известна а – поправка (или систематическая ошибка), то из результата измерений вычитаем а:

μ= -а. (4)

Зам.: 1. Если , то существенны только случайные ошибки.

2. Если случайные ошибки распределены по нормальному закону, то можно построить доверительные интервалы для коэффициента доверия α.

Окончательный результат представляется в виде:

1) , вероятность P=α; 2) : σ_Σ=…; ; n=…. Причем форма 1) работает, когда пренебрегают систематическими ошибками, 2) когда учитываются случайные и систематические ошибки.

1.4. Косвенные измерения

В случае косвенных измерений искомая величина z вычисляется по уравнению

z=f(x, y, …, a, b, …), (1)

где z- измеряемая величина, x, y, … - результаты прямых измерений, a, b, …- физические постоянные приборов измерений.

Для простоты изложения будем иметь , где -значение функции от выборочного значения среднего аргумента . Кроме того, пусть μ_x- истинное значение x.

Тогда представим

, (2)

Причем

. (3)

Разложение (2) предполагает, что для всех

. (4)

Связь (4) определяет интервал , для которого справедлива (2), т.е.

. (5)

Чтобы (5) было справедливо, необходимо определить верхнюю границу для СВ ( ), т.е. .

Рассмотрим случай, когда для результата прямого измерения существенны системные, случайные и приборные ошибки ( ) :

. (6)

Если α<0.8÷0.9, то

, (7)

где - предельная ошибка прибора, для оценки стандартного отклонения случайных ошибок имеем:

,

а различные системные ошибки представляются

.

Если СлО велики, то будет верхней границей. Если СлО малы, то ими можно пренебречь. Тогда окончательно (5) будет

. (8)

Для проверки (8) имеем 2 случая.

1. (8) не выполнимо. Разложение (2) нельзя применять для оценки .

2. (8) работает. Тогда

, (9)

где .

Согласно - для левой части (9),

- для правой части (9),

имеем , т.е. среднее значение функции от выборочного среднего значения аргумента равно искомому значению функции. Поэтому величина при выполнении (2) принимается за оценку μ_z.

Для определения возможных ошибок в запишем (6) в виде

. (10)

Подставляя (10) в (9) и возводя в квадрат, имеем

. (11)

Пусть

, (12)

где первое слагаемое отвечает за системные ошибки, второе – за случайные.

Таким образом, из (11) с учетом (12), имеем:

. (13)

Зам.: Соотношение (13) применяется для оценки стандартных отклонений различных систематических ошибок.

Для получения оценки стандартного отклонения СлО рассмотрим выражения:

. (14)

За оценку стандартного отклонения СлО примем:

. (15)

Кроме того, для случая, если

, (16)

то (13), (15) преобразуются

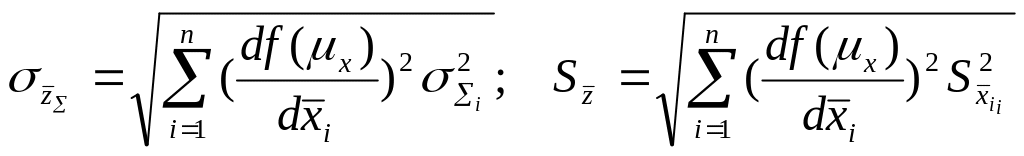. (17)

Таким образом, полученные формулы (13), (15), (17) позволяют учесть ошибки косвенных измерений, при этом необходима последовательность действий по методике:

1. результаты измерений записываются в таблицу

2. для результатов прямых измерений (где i- номер аргумента) функции f надо вычислить

а) выборочно значение

б) выборочное значение стандартных отклонений

3. для каждого аргумента определить

а) суммарные системные ошибки

б) интервалы

.

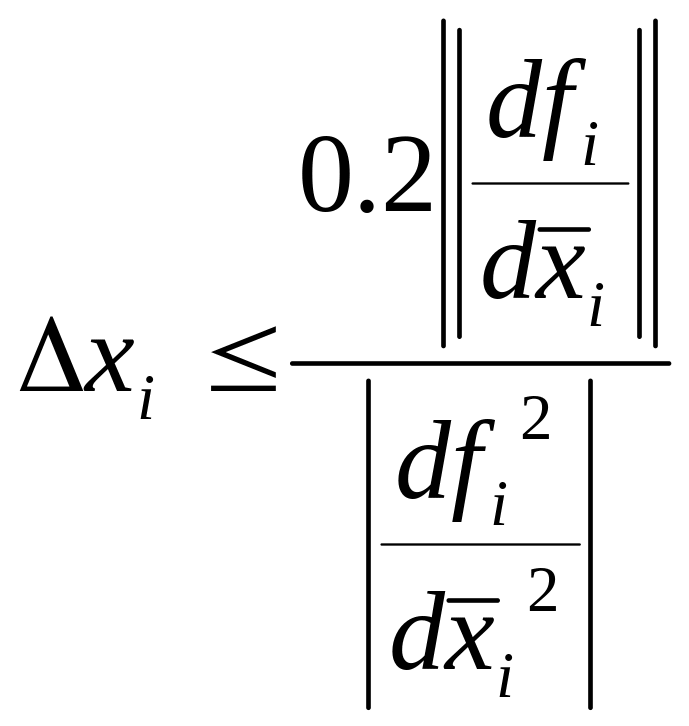4. Проверяем условие 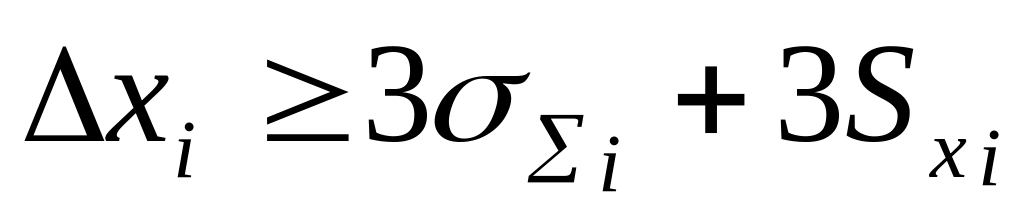. Если «да», то действие 5), “нет” – измерения продолжают до тех пор пока условие не будет выполняться.

5. Вычисляем значение функции

.

6. вычисляем стандартное отклонение системных и случайных ошибок

.

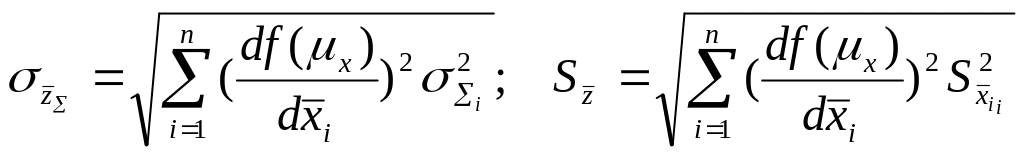7. задаем коэффициент доверия α. Окончательный результат записываем в виде:

а) , вероятность P=α, если СлО

малы;

б) когда учитываются случайные и систематические ошибки.

Зам.: при совместных измерениях используют метод наименьших квадратов.

Пример.