4.4. Функция распределения.

Функция распределения случайной величины – это функция действительной переменной , определяющая вероятность того, что случайная величина принимает значение меньше некоторого фиксированного числа , т.е. :

где – плотность распределения вероятностей.

Плотностью распределения непрерывной случайной величины Х называют предел, если он существует, отношения вероятности попадания случайной величины Х на отрезок , примыкающей к точке , к длине этого отрезка, когда последний стремится к 0, т.е.

.

При этом вероятность попадания значений случайной величины Х в интервал равна определенному интегралу от плотности распределения по отрезку :

Иногда вместо термина «функция распределения» используют термин «интегральная функция».

Для дискретной случайной величины функции распределения вычисляются по формуле:

График функции распределения дискретной случайной величины имеет ступенчатый вид. Убедимся в этом на примере.

Пример 4.6. Закон распределения дискретной случайной величины задан следующей таблицей:

Х	0	1	2	3
Р	0,2	0,4	0,3	0,1

Найти функцию распределения.

Решение:

При

При

При

При

При

Итак, функция распределения аналитически может быть записана так:

Изобразим график функции .

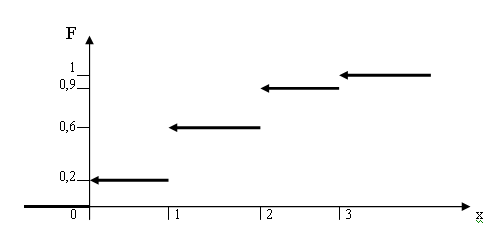
Рис. 4.2. График функции распределения

Свойства функции распределения

1. Значения функции распределения принадлежат отрезку [0,1].

2. F (х) – неубывающая функция, т. е. F (x₂) > F (x₁), если х₂ > х₁.

Следствие. Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b),равна приращению функции распределения на этом интервале:

P(a < X < b) = F(b) – F (a).

3. Если возможные значения случайной величины принадлежат интервалу (а, b), то:

1) F(x) = 0, при ;

2) F (х) = 1 при .

4.5. Математическое ожидание случайной величины

Как уже известно, закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины.

К числу важных числовых характеристик относится математическое ожидание.

Математическое ожидание приближенно равно среднему значению случайной величины.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Если случайная величина характеризуется конечным рядом распределения:

Х	х1	х2	х3	…	хп
Р	р1	р2	р3	…	рп

то математическое ожидание М(Х) определяется по формуле:

или

Математическое ожидание непрерывной случайной величины определяется равенством:

,

где – плотность вероятности случайной величины Х.

Пример 4.7. Найти математическое ожидание числа очков, выпадающих при бросании игральной кости.

Решение:

Случайная величина Х принимает значения 1, 2, 3, 4, 5, 6. Составим закон ее распределения:

Х	1	2	3	4	5	6
Р

Тогда математическое ожидание равно: