5.2. Распределение Пуассона.

Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, непоявления q = 1 – p.

Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях.

Поставим перед собой задачу: найти закон распределения величины X.

Если число испытаний велико, а вероятность появления события в каждом испытании мала, то вероятность того, что некоторое событие появиться k раз в испытаниях, приближенно вычисляется по формуле:

,

где – число появлений событий в независимых испытаниях,

– среднее число появлений событий в испытаниях.

Случайная величина, характеризующая число наступлений события в независимых испытаниях, распределена по закону Пуассона, если

Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона:

Замечание. Имеются специальные таблицы, пользуясь которыми можно найти , зная k и (Приложение 2).

Пример 5.2. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.

Решение.

По условию, п = 5000, р = 0,0002, k = 3.

Найдем :

По формуле Пуассона искомая вероятность приближенно равна:

5.3. Равномерное распределение

Распределение вероятностей случайной величины Х называется равномерным на отрезке , если плотность вероятности равна нулю всюду, кроме отрезка , на котором все значения случайной величины Х одинаково возможны.

Выражение плотности распределения вероятностей имеет следующий вид:

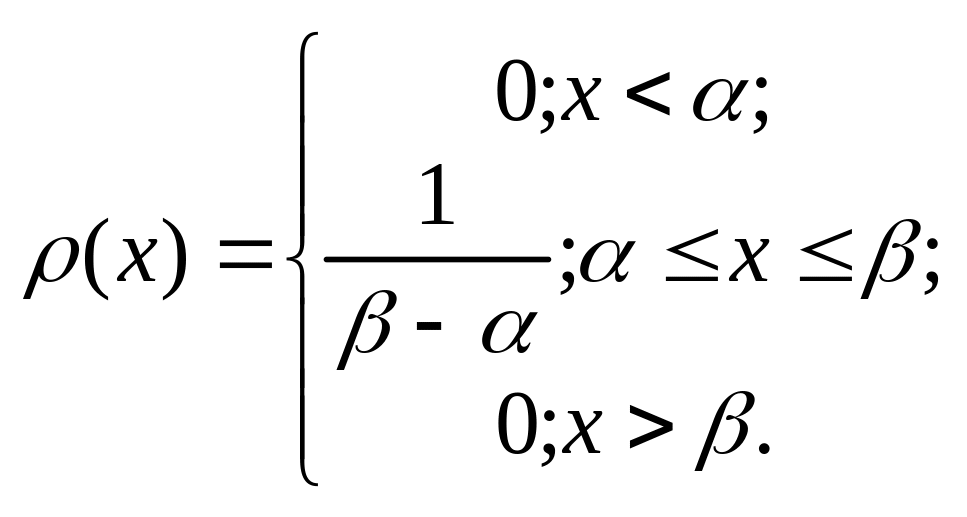
Функция равномерного распределения задается формулой:

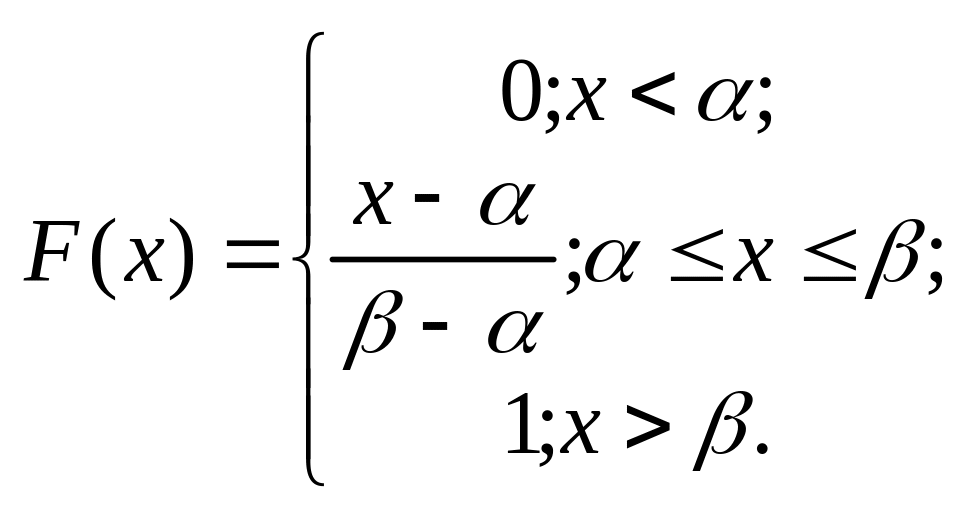
Напомним, что вероятность попадания значений случайной величины Х в интервал равна определенному интегралу от плотности распределения по отрезку :

Математическое ожидание, дисперсия и среднее квадратическое отклонение соответственно равны:

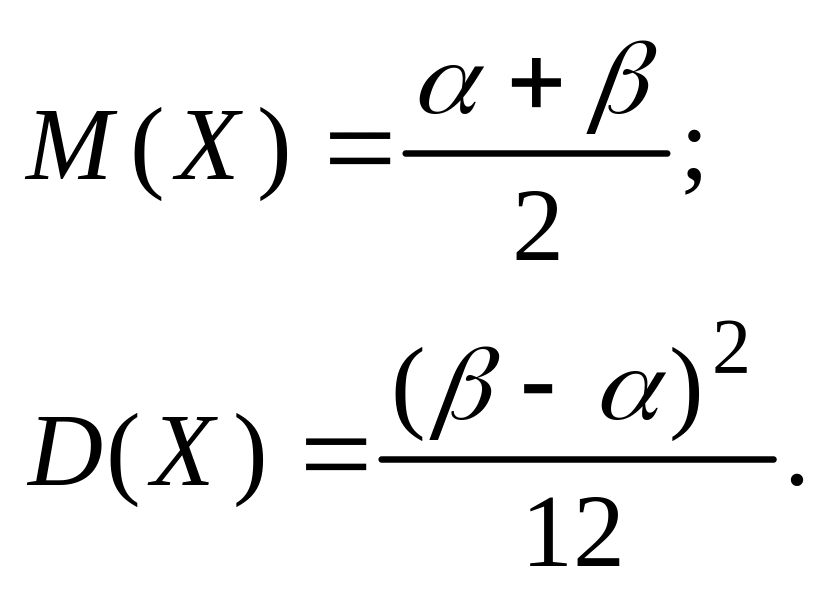
5.4. Нормальное распределение.

Распределение с непрерывной случайной величины называется нормальным, если плотность распределения ее описывается формулой:

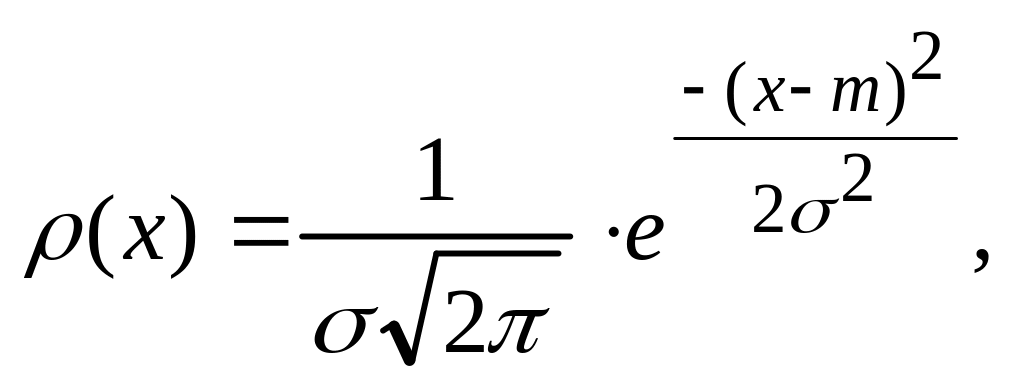
где – параметры нормального распределения.

Функция распределения случайной величины Х, распределенной по нормальному закону:

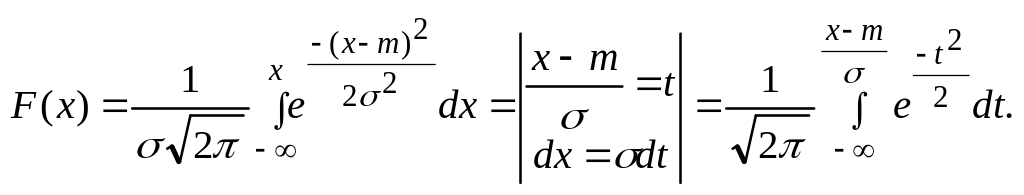
Полученный интеграл нельзя выразить через элементарные функции, но его можно вычислить через специальную функцию:

называемую нормальной функцией распределения (функцией Лапласа).

Эта функция неубывающая, непрерывная и

Вероятность попадания случайной величины , подчиненной нормальному закону распределения, на заданный интервал , определяется следующим образом:

где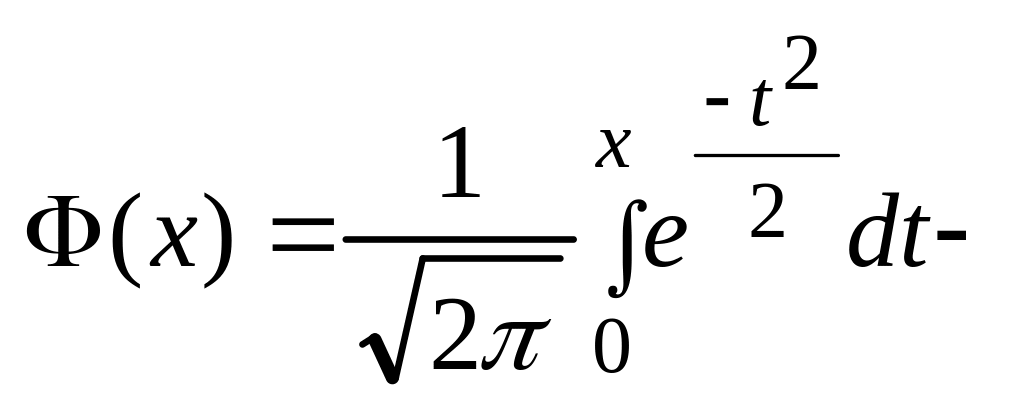 функция Лапласа.

Замечание. Имеются специальные таблицы, пользуясь которыми можно найти значения функции Лапласа (Приложение 1).

Вероятность заданного отклонения вычисляется по формуле:

Математическое ожидание и дисперсия соответственно равны:

Правило трех сигм: Интервалом практически возможных значений случайной величины , распределенной по нормальному закону, будет интервал .