6.3. Функция распределения двумерной случайной величины

Функцией распределения двумерной случайной величины (X, Y) называют функцию F (х, у), определяющую для каждой пары чисел х, у вероятность того, что X примет значение, меньшее х, и при этом У примет значение, меньшее у:

F(x,y) = P(X < x, Y < y).

Геометрически это равенство можно истолковать так:

F (х, у) есть вероятность того, что случайная точка (X, Y) попадет в бесконечный квадрант с вершиной (х, у), расположенный левее и ниже этой вершины.

Свойства функции распределения двумерной случайной величины

1. Значения функции распределения удовлетворяют двойному неравенству:

2. F (х, у) есть неубывающая функция по каждому аргументу.

3. Имеют место предельные соотношения:

1) 2)

3) 4)

4. При 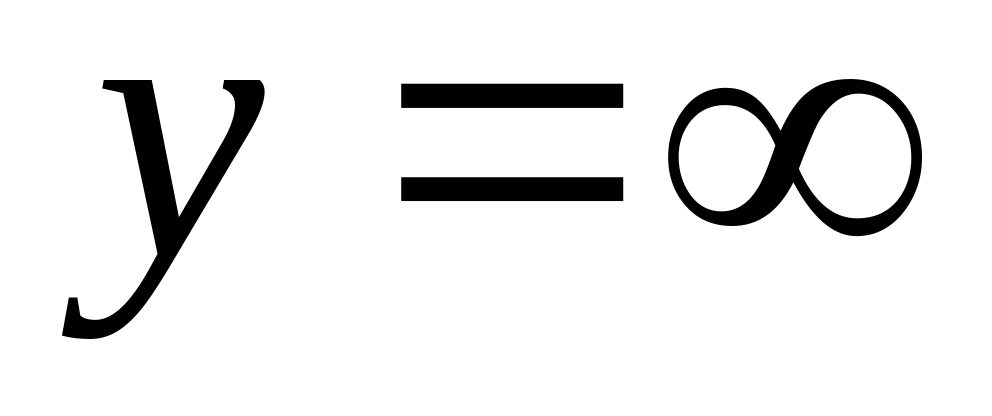функция распределения системы становится функцией распределения составляющей X:

.

При функция распределения системы становится функцией распределения составляющей У:

.

6.4. Плотность непрерывной двумерной случайной величины

Двумерная случайная величина задавалась с помощью функции распределения. Непрерывную двумерную величину можно также задать, пользуясь плотностью распределения.

Будем предполагать, что функция распределения F (х, у) всюду непрерывна и имеет всюду (за исключением, быть может, конечного числа кривых) непрерывную частную производную второго порядка.

Плотностью совместного распределения вероятностей f(х, у) двумерной непрерывной случайной величины (X, Y) называют вторую смешанную частную производную от функции распределения:

Геометрически эту функцию можно истолковать как поверхность, которую называют поверхностью распределения.

Зная плотность распределения, можно найти функцию распределения по формуле:

Вероятность попадания случайной точки (Х,Y) в область D определяется равенством

6.5. Числовые характеристики непрерывной системы двух случайных величин

Зная плотности распределения составляющих Х и У непрерывной двумерной случайной величины (X, У), можно найти их математические ожидания и дисперсии:

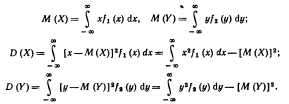
Начальным моментом v_k,s порядка k + s системы (X, Y) называют математическое ожидание произведения X^kY^s:

v_k,s = М[X^kY^s].

Центральным моментом µ_k,s порядка k + s системы (X, Y) называют математическое ожидание произведения отклонений соответственно k-й и s-й степеней:

µ_k,s = М{[X – M(X)]^{k .} [Y –M(Y)]^s}.

Корреляционным моментом µ_ху системы (X, Y) называют центральный момент µ_1,1 порядка 1 + 1:

µ_х,у = М{[X – M(X)] ^. [Y –M(Y)]}.

Коэффициентом корреляции величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:

Коэффициент корреляции служит для оценки тесноты линейной связи между X и Y: чем ближе абсолютная величина коэффициента корреляции к единице, тем связь сильнее; чем ближе абсолютная величина коэффициента корреляции к нулю, тем связь слабее.

Коррелированными называют две случайные величины, если их корреляционный момент отличен от нуля.

Некоррелированными называют две случайные величины, если их корреляционный момент равен нулю.