14.2. Геометрические свойства производных полиномов бернштейна

14.2.1. Вычисление первой производной

Возьмем производную полинома Бернштейна  -го порядка:

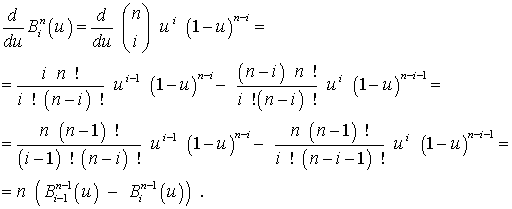
Таким образом, окончательно получаем формулу для вычисления первой производной полиномов Бернштейна:

.

( 13 )

Тогда для кривой Безье формула первой производной имеет вид

.

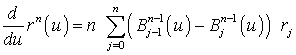Так как  для, то

и

.

Окончательно получаем формулу для вычисления первой производной кривой Безье:

.

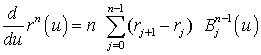Форму записи последней формулы можно упростить, если использовать оператор разности  :

.

( 14 )

Тогда формула первой производной принимает вид

.

( 15 )

С геометрической точки зрения, производной кривой Безье является другая кривая Безье  , векторы управляющих точек которой определяются вычислением разностей векторов управляющих точек исходной кривой. Кривая первой производнойиногда называется первым годографом кривой Безье. Векторы характеристической ломаной годографа определяются следующим образом (см.рис. 14.2):

.

Начальный вектор  выбирается произвольно, в ряде случаев удобно выбрать.

 

 

 

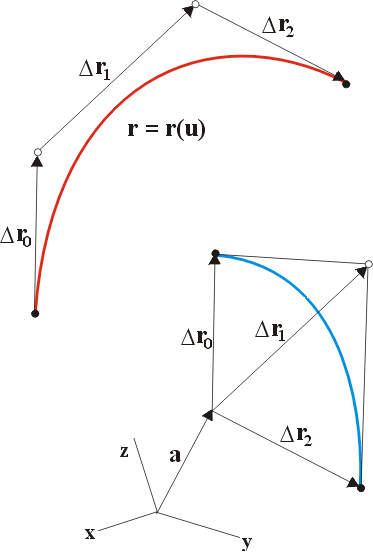
Рис. 14.2. Кубическая кривая Безье и ее первый годограф

14.2.2. Вычисление производных высшего порядка

Так же, как и для случая первой производной, введем итерационный оператор разностей  , определяемый с помощью выражения

( 16 )

Пример

.

Стоящие в правой части выражения ( 16 ) члены представляют собой биномиальные коэффициенты, которые представляются в общем виде с помощью выражения

.

( 17 )

Тогда формула для вычисления  -ой производной кривой Безье запишется как

.

( 18 )

Доказательство формулы ( 18 ) очевидно и вытекает из многократного дифференцирования ( 15 ).

Запишем два важных частных случая формулы ( 18 ) для  и:

( 19 )

и

.

( 20 )

С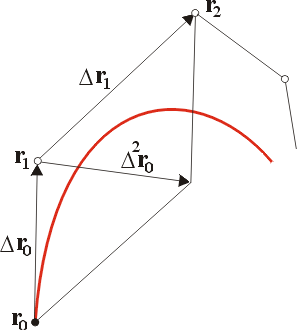ледовательно,-ая производная кривой Безье в крайних точках дуги зависит только отближайших управляющих точек, включая саму крайнюю точку. Дляочевидно, что векторыиопределяют касательную в точке с параметром. В общем случае касательная в точкеопределяется вектороми первым вектором, отличным от. Таким образом, касательная в точкеможет быть определена даже в том случае, если касательный вектор равен нулю. Для другого конца дугирассуждения аналогичны. Нарис. 14.3 показаны примеры определения векторов первой и второй производных в начальной точке дуги кривой .

Рис. 14.3. - Определение векторов первой и второй производных

14.3. Методы полиномиальной аппроксимации двумерных обводов

Вышерассмотренные методы достаточно просто обобщаются на случай аппроксимации двумерных обводов. Для конструирования криволинейных поверхностей с помощью стандартных параметрических полиномов, полиномов Бернштейна и NURBS в современных системах геометрического моделирования применяют три основных метода:

• тензорного произведения (tensor product surfaces);

• каркасный (lofting surfaces);

• булевой суммы (transfinite method).

Рассмотрим возможности этих методов, взяв в качестве базового геометрического описания рациональные параметрические кривые Безье (частный случай NURBS).
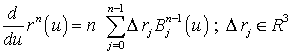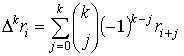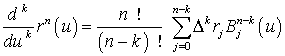