13.1.2. Барицентрические координаты на плоскости

Рассмотрим метод барицентрических координат на плоскости. Пусть в пространстве задан треугольники произвольная точка. Координаты точкизапишем как барицентрическую комбинацию координат точек:

, ,

( 2 )

где - барицентрические координаты точкиотносительно треугольника, который называется базисным, или координатным. Его вершины имеют следующие барицентрические координаты:,,. Точки, лежащие на отрезке, имеют координаты

, гдеи,.

Применяя геометрический подход к понятию барицентрических координат, выразим их через площади некоторых треугольников. Сначала рассмотрим случай, когда точка лежит внутри треугольника. Здесь справедлива следующая теорема.

Теорема.Пусть точка(рис. 3) лежит внутри базисного треугольникаи пусть- площади треугольников,,,. Тогда барицентрические координаты точкиравны

.

( 3 )

Для вычисления площадей этих треугольников воспользуемся векторным представлением их вершин. Выберем точку за начало радиус-векторов и обозначим радиус-векторы точекчерез. Тогда

,

                    или

,

где знак обозначает внешнее произведение векторов.

Внешнее произведение двух векторов ивыражается формулой

,

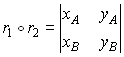следовательно,

,

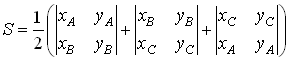                    или

.

( 4 )

    Вычисление барицентрических координат точки можно свести к вычислению площадей треугольников и в том случае, если точка лежит вне координатного треугольника или на его границе. Для этого необходимо ввести понятие ориентированного треугольника, когда кроме задания его вершин также задается направление их обхода. Если обход производится "против часовой стрелки", то треугольник ориентирован положительно, если "по часовой стрелке" - отрицательно. В соответствии с этим определяется ориентированная площадь треугольника, которая будет при этом положительной или отрицательной, а также нулевой, если базисные точки коллинеарные. Именно поэтому в правой части уравнения ( 4 ) необходимо поставить знак .

Для корректности уравнений ( 3 ) необходимо, чтобы площадь , т.е. точкидолжны быть неколлинеарными.

Барицентрические координаты на плоскости, как и на прямой, обладают свойством аффинной инвариантности. Таким образом, любые три неколлинеарные точки определяют на плоскости барицентрическую систему координат.

 

Рис. 13.3. Определение барицентрических координат через площади треугольников

Мы используем барицентрические координаты для определения линейной интерполяции трех неколлинеарных точек. Предположим, что в пространстве заданы три точки. Любая точка, координаты которой вычислены с помощью уравнения

,,

(5)

лежит в плоскости, определяемой этими точками. Это отображение пространствана пространствобудет линейной интерполяцией трех точек. Так как, томожно считать барицентрическими координатами точкиотносительно заданных точек. Также можно считатьбарицентрическими координатами точки, принадлежащей, относительно некоторого треугольника. Следовательно, уравнение ( 5 ) можно интерпретировать как отображение треугольникана треугольник.
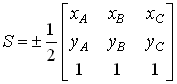