13.3. Аппроксимация поверхностей обобщенными полиномами бернштейна

13.3.1. Свойства треугольной порции поверхности безье

Треугольные порции поверхности являются естественным обобщением метода барицентрических координат на плоскости. Произвольная точка,инцидентная такой порции поверхности,может быть определена с помощью повторяющейся линейной интерполяции. Применяемые при этом алгоритмы линейной интерполяции являются обобщением алгоритмов для одномерного случая. Следовательно, сохранятся и важные свойства геометрических фигур, конструируемых с помощью линейной интерполяции.

Отметим эти свойства конструируемых треугольных порций поверхности:

1. Поверхности в общем случае принадлежат только три точки характеристического многогранника с барицентрическими координатами (0, 0, 1), (0, 1, 0) и (1, 0, 0).

2. Аффинная инвариантность. Это свойство вытекает из того, что в алгоритме используется линейная интерполяция, являющаяся аффинным преобразованием пространства.

3. Инвариантность при аффинных преобразованиях параметра.

4. Треугольная порция поверхности лежит в выпуклой оболочке своего характеристического многогранника.

Это свойство подтверждается тем, что любая точка ,определяется с помощью линейной комбинации предыдущих точек.

5. Образом произвольной прямой в плоскости параметров является кривая-го порядка на треугольной порции поверхности [3]. Это весьма важное отличие треугольных порций от топологически прямоугольных порций поверхностей тензорного произведения.

13.3.2. Свойства обобщенных полиномов бернштейна

Треугольную порцию поверхности можно определить, используя обобщенные полиномы Бернштейна:

,

(11)

 где      - барицентрические координаты,

,,.

Сумма полиномов, определенных на заданном интервале, равна единице

Свойства обобщенных полиномов Бернштейна сходны со свойствами одномерных полиномов:

1. Сумма полиномов, определенных на заданном интервале, равна единице . Это свойство обеспечивает инвариантность полиномов при аффинных преобразованиях. Следовательно, аффинно инвариантны и треугольные порции поверхностей Безье, определяемые этим набором полиномов. Заметим, что выше мы доказали это свойство, используя геометрическую интерпретацию.

2. Все полиномы положительны на заданном интервале

.

3. Возможно рекурсивное вычисление полиномов степени , если известны полиномы степени:

,.

Пример Запишем формулы обобщенных полиномов Бернштейна для случая и представим результаты в виде схемы (Рис. 10). На рис. 11 и рис. 12 показан вид некоторых базисных полиномов треугольной кубической порции поверхности.

Рис. 13.10. Формулы обобщенных кубических полиномов Бернштейна

Рис. 13.11. Семейство кубических обобщенных полиномов Бернштейна

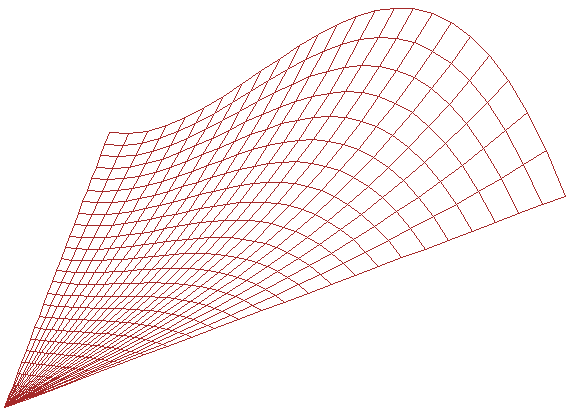
Рис. 13.12. Примеры обобщенных кубических полиномов Бернштейна

Мы рассмотрели алгоритм определения точки, инцидентной треугольной порции поверхности, с заданными барицентрическими координатами на основе повторяющейся линейной интерполяции. Решим эту задачу, используя обобщенные полиномы Бернштейна и их свойства.

Запишем уравнение (10) в виде

                     

                                       

                                       

                                        .

    Таким образом, каждый шаг алгоритма связан с линейной интерполяцией, определяемой формулой

.

( 12 )

Подставляя в уравнение ( 12 ) , получим уравнение треугольной порции поверхности Безье, определенной с помощью обобщенных полиномов Бернштейна:

( 13 )

                    или

.

Угловые точки порции поверхности задаются векторами ,и.

Граничные кривые определяются характеристическими ломаными:

;

;

.

    Так же, как и для одномерного случая, перемещение любой из управляющих точек влияет на форму поверхности в окрестности этой точки. Пример сконструированной кубической треугольной порции поверхности показан на рис. 13.13 .

Рис. 13.13. Кубическая треугольная порция поверхности Безье и ее характеристический многогранник