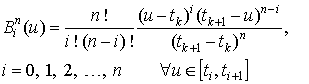- •Введение
- •1. Модели. Элементы моделей
- •2. Построение кривых
- •3. Построение поверхностей
- •4. Типы моделей
- •5. Полигональные сетки
- •6. Описание геометрических форм
- •6.1. Описание поверхностей. Параметрическое описание поверхностей
- •Эллипсоид
- •Xacoscos,
- •Общие случаи нормали к поверхности
- •Описание поверхностей неявными функциями
- •6.2. Поточечное описание поверхностей.
- •6.3. Синтез изображений методом обратной трассировки лучей
- •Система координат, применяемая в методе обратной трассировки лучей
- •6.4. Способы представления моделей геометрических объектов
- •6.5. Кривые и поверхности nurbs
- •7. Структура твердотельной модели
- •8. Синтез твердого тела по процедурному описанию
- •8.1 Векторная полигональная модель
- •8.2. Воксельная модель
- •8.3. Равномерная сетка
- •8.4. Неравномерная сетка. Изолинии
- •9. Преобразование моделей описания поверхности
- •10. Понятие кубических сплайнов
- •11. Интерполяция b-сплайнами
- •12. Выпуклые оболочки
- •Основные понятия и идеи
- •12.1. Метод обхода грэхема
- •12.2. Обход методом джарвиса
- •13. Геометрмческое моделирование криволинейных объек тов с использованием барицентрических координат
- •13.1. Линейная интерполяция и барицентрические координаты
- •13.1.1. Барицентрические координаты на прямой
- •13.1.2. Барицентрические координаты на плоскости
- •13.1.3. Барицентрические координаты в пространстве
- •13.2. Метод определения точек, инцидентных треугольной порции поверхности, по заданным локальным координатам
- •13.2.1. Алгоритм задания квадратичной параболы
- •13.2.2. Анализ алгоритма кастельжо для произвольной кривой
- •13.2.3. Обобщённый алгоритм для треугольной порции поверхности
- •13.3. Аппроксимация поверхностей обобщенными полиномами бернштейна
- •13.3.1. Свойства треугольной порции поверхности безье
- •13.3.2. Свойства обобщенных полиномов бернштейна
- •14. Особенности аппроксимации обводов параметрическими полиномами в форме бернштейна
- •14.1. Методы полиномиальной аппроксимации одномерных обводов
- •14.1.1. Общая постановка задачи аппроксимации дискретного набора данных
- •14.1.2. Аппроксимация обводов параметрическими полиномами
- •14.1.3. Аппроксимация обводов параметрическими полиномами бернштейна
- •14.2. Геометрические свойства производных полиномов бернштейна
- •14.2.1. Вычисление первой производной
- •14.2.2. Вычисление производных высшего порядка
- •14.3. Методы полиномиальной аппроксимации двумерных обводов
- •Метод тензорного произведения
- •Каркасный метод
- •14.3.3. Метод булевой суммы (поверхности Кунса)
- •15. Стандарты в графических системах сапр и современные растровые графические файлы
- •15.1. Графические системы класса 2d
- •15.2. Графические системы класса 3d
- •15.3. Стандарты обмена данными
- •16. Системы подготовки и выпуска конструкторско-технологической документации. Организация конструкторской подготовки производства
- •17. Графические диалоговые системы
- •17.1. Краткий обзор зарубежных cad-систем
- •Технологические модули в pt/Products. Интеграция процессов проектирования и изготовления
- •Работа со стандартными библиотеками посредством pt/LibraryAccess и pt/Library
- •17.2. Отечественные разработки
- •Компас 5
- •T-flex cad
- •Заключение
- •394026 Воронеж, Московский просп., 14
14.1.3. Аппроксимация обводов параметрическими полиномами бернштейна
Итак, другой распространенной формой представления полиномов является представление в форме Бернштейна. Кроме аспектов, связанных с вычислительной устойчивостью алгоритмов с участием полиномов в форме Бернштейна, этот вид представления полиномов имеет несомненные преимущества чисто с геометрической точки зрения. Рассмотрим "геометрические" свойства полиномов Бернштейна более подробно.
Произвольный
полином степени
![]() в
форме Бернштейна определяется уравнением
в
форме Бернштейна определяется уравнением
|
|
(11) |
где
![]() -
коэффициенты Бернштейна,
-
коэффициенты Бернштейна,
![]() -
скалярные функции Бернштейна.
-
скалярные функции Бернштейна.
Коэффициенты
![]() могут
быть скалярными значениями некоторой
функции
могут
быть скалярными значениями некоторой
функции![]() ,
вычисленными на некотором отрезке
,
вычисленными на некотором отрезке![]() для
равноотстоящих точек. Тогда полином
для
равноотстоящих точек. Тогда полином![]() аппроксимирует
функцию
аппроксимирует
функцию![]() при
достаточно больших
при
достаточно больших![]() .
Если заменить скалярные коэффициенты
.
Если заменить скалярные коэффициенты![]() произвольными
векторами
произвольными
векторами![]() ,
то в этом случае полином
,
то в этом случае полином![]() аппроксимирует
ломаную, вершинами которой является
заданный набор векторов
аппроксимирует
ломаную, вершинами которой является
заданный набор векторов![]() ,
и определяет на заданном отрезке
,
и определяет на заданном отрезке![]() дугу
кривой Безье
дугу
кривой Безье![]() -го
порядка. Изменяя положение векторов,
можно управлять формой дуги кривой.
-го
порядка. Изменяя положение векторов,
можно управлять формой дуги кривой.
Скалярные
функции
![]() определяются
уравнениями
определяются
уравнениями
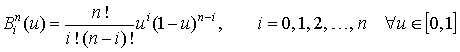
и образуют так
называемый базис Бернштейна для множества
всех полиномов степени не выше
![]() на
отрезке
на
отрезке![]() .
Например, для случая
.
Например, для случая![]() изображены
функции базиса Бернштейна (см.рис.
14.1).
изображены
функции базиса Бернштейна (см.рис.
14.1).
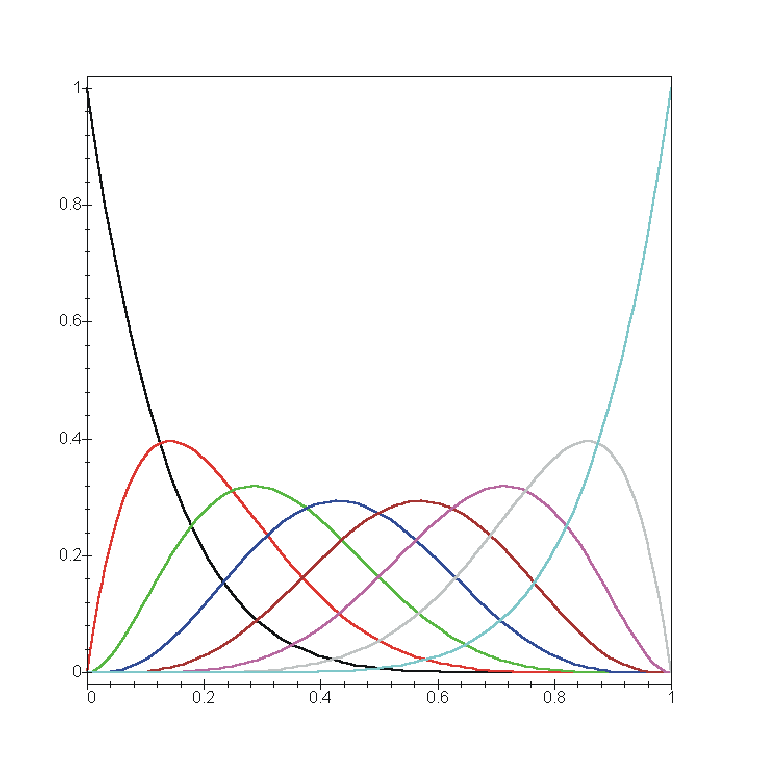
Рис. 14.1. Полиномы Бернштейна степени 7
В ряде случаев
вместо единичного отрезка
![]() изменения
параметра целесообразно использовать
отрезок
изменения
параметра целесообразно использовать
отрезок![]() . Тогда
значения локального параметра
. Тогда
значения локального параметра![]() на
этом общем отрезке
на
этом общем отрезке![]() можно
вычислить по формуле:
можно
вычислить по формуле:
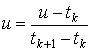 .
.
На отрезке
![]() базисные функции Бернштейна
определяются уравнениями
базисные функции Бернштейна
определяются уравнениями
|
|
(12) |
Отметим следующие основные свойства полиномов Бернштейна:
Сумма полиномов, определенных на заданном отрезке, равна единице:
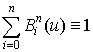 ,
,![]() .
Это
свойство обеспечивает инвариантность
полиномов при аффинных преобразованиях.
Следовательно, аффинно-инвариантны
и кривые Безье, определяемые этим набором
полиномов. Заметим, что этим
свойством обладают также полиномы
в форме Лагранжа ( 8 ) и Эрмита ( 9 ), но не
обладают стандартные полиномы ( 1 ).
.
Это
свойство обеспечивает инвариантность
полиномов при аффинных преобразованиях.
Следовательно, аффинно-инвариантны
и кривые Безье, определяемые этим набором
полиномов. Заметим, что этим
свойством обладают также полиномы
в форме Лагранжа ( 8 ) и Эрмита ( 9 ), но не
обладают стандартные полиномы ( 1 ).
Все полиномы не отрицательны на заданном отрезке
![]() ,
,![]() .
.
В работе [3]
указано, что значения полинома
![]() находятся
в интервале
находятся
в интервале
![]() .
Это
означает, что кривая, определяемая
полиномом
.
Это
означает, что кривая, определяемая
полиномом![]() ,
лежит внутри выпуклой оболочки
коэффициентов
,
лежит внутри выпуклой оболочки
коэффициентов![]() . Часто
это свойство называют "свойством
выпуклости оболочки". Заметим, что
на плоскости выпуклая оболочка представляет
собой область, ограниченную выпуклой
ломаной, а в пространстве – выпуклым
многогранником.
. Часто
это свойство называют "свойством
выпуклости оболочки". Заметим, что
на плоскости выпуклая оболочка представляет
собой область, ограниченную выпуклой
ломаной, а в пространстве – выпуклым
многогранником.
Возможно рекурсивное вычисление полиномов степени
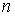 ,
если известны полиномы степени
,
если известны полиномы степени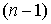 :
:
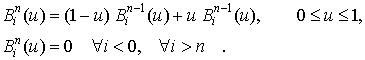
Это свойство
используется для вычисления
![]() с
помощью повторяющейся линейной
интерполяции.
с
помощью повторяющейся линейной
интерполяции.
Если
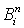 -
полиномы Бернштейна степени
-
полиномы Бернштейна степени ,
то полиномы
,
то полиномы степени
степени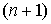 вычисляются с
помощью выражения:
вычисляются с
помощью выражения:
![]() ,
,
где
![]() для
для![]() .
.
![]() ,
,![]() .
Это
свойство используется при аппроксимации
кривой Безье
.
Это
свойство используется при аппроксимации
кривой Безье![]() -го
порядка другой кривой порядка
-го
порядка другой кривой порядка![]() .
.
В работе [2] доказано, что полиномы Бернштейна лучше приспособлены для вычисления простых корней, чем степенные полиномы, как на единичном отрезке
 ,
так и на отрезке
,
так и на отрезке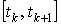 .
Полиномы в форме Бернштейна обладают
большей вычислительной устойчивостью,
чем степенные полиномы. Это связано
с тем, что при вычислении степенных
полиномов по схеме Горнера может
происходить значительная потеря
точности за счет вычитания близких
больших по модулю округленных чисел.
При этом потеря точности увеличивается
с возрастанием
.
Полиномы в форме Бернштейна обладают
большей вычислительной устойчивостью,
чем степенные полиномы. Это связано
с тем, что при вычислении степенных
полиномов по схеме Горнера может
происходить значительная потеря
точности за счет вычитания близких
больших по модулю округленных чисел.
При этом потеря точности увеличивается
с возрастанием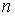 из-за
ограниченного числа цифровых разрядов
компьютера. Избежать потери точности
в этом случае удается, применяя для
вычисления полинома рекуррентные
формулы. Один из методов измерения
вычислительной устойчивости алгоритмов
заключается в сравнении оценок
погрешностей значения полинома в
различных формах представления в
окрестности произвольной точки [7].
В работе [5]
выполнено исследование вычислительных
аспектов алгоритмов полиномиальной
аппроксимации и доказано, что полиномы в
форме Бернштейна имеют меньшую оценку
погрешности, чем степенные полиномы в
стандартной форме. Однако при
выполнении преобразования из одной
формы представления полинома в другую
указанное свойство может теряться
из-за появления вычислительной
неустойчивости.
из-за
ограниченного числа цифровых разрядов
компьютера. Избежать потери точности
в этом случае удается, применяя для
вычисления полинома рекуррентные
формулы. Один из методов измерения
вычислительной устойчивости алгоритмов
заключается в сравнении оценок
погрешностей значения полинома в
различных формах представления в
окрестности произвольной точки [7].
В работе [5]
выполнено исследование вычислительных
аспектов алгоритмов полиномиальной
аппроксимации и доказано, что полиномы в
форме Бернштейна имеют меньшую оценку
погрешности, чем степенные полиномы в
стандартной форме. Однако при
выполнении преобразования из одной
формы представления полинома в другую
указанное свойство может теряться
из-за появления вычислительной
неустойчивости. Полиномы Бернштейна
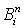 имеют
максимум при значении параметра
имеют
максимум при значении параметра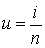 .
Это свойство используется при локальном
контроле формы обвода. Перемещение
управляющей точки
.
Это свойство используется при локальном
контроле формы обвода. Перемещение
управляющей точки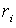 кривой
Безье в большей мере затрагивает участок
кривой в окрестности точки со значением
параметра
кривой
Безье в большей мере затрагивает участок
кривой в окрестности точки со значением
параметра .
.Полиномы Бернштейна могут быть вычислены по схеме Горнера с помощью следующих формул:
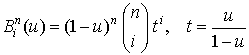 на отрезке
на отрезке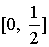 ;
; на отрезке
на отрезке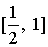 .
.

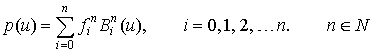 .
.