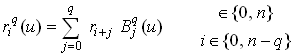- •Введение
- •1. Модели. Элементы моделей
- •2. Построение кривых
- •3. Построение поверхностей
- •4. Типы моделей
- •5. Полигональные сетки
- •6. Описание геометрических форм
- •6.1. Описание поверхностей. Параметрическое описание поверхностей
- •Эллипсоид
- •Xacoscos,
- •Общие случаи нормали к поверхности
- •Описание поверхностей неявными функциями
- •6.2. Поточечное описание поверхностей.
- •6.3. Синтез изображений методом обратной трассировки лучей
- •Система координат, применяемая в методе обратной трассировки лучей
- •6.4. Способы представления моделей геометрических объектов
- •6.5. Кривые и поверхности nurbs
- •7. Структура твердотельной модели
- •8. Синтез твердого тела по процедурному описанию
- •8.1 Векторная полигональная модель
- •8.2. Воксельная модель
- •8.3. Равномерная сетка
- •8.4. Неравномерная сетка. Изолинии
- •9. Преобразование моделей описания поверхности
- •10. Понятие кубических сплайнов
- •11. Интерполяция b-сплайнами
- •12. Выпуклые оболочки
- •Основные понятия и идеи
- •12.1. Метод обхода грэхема
- •12.2. Обход методом джарвиса
- •13. Геометрмческое моделирование криволинейных объек тов с использованием барицентрических координат
- •13.1. Линейная интерполяция и барицентрические координаты
- •13.1.1. Барицентрические координаты на прямой
- •13.1.2. Барицентрические координаты на плоскости
- •13.1.3. Барицентрические координаты в пространстве
- •13.2. Метод определения точек, инцидентных треугольной порции поверхности, по заданным локальным координатам
- •13.2.1. Алгоритм задания квадратичной параболы
- •13.2.2. Анализ алгоритма кастельжо для произвольной кривой
- •13.2.3. Обобщённый алгоритм для треугольной порции поверхности
- •13.3. Аппроксимация поверхностей обобщенными полиномами бернштейна
- •13.3.1. Свойства треугольной порции поверхности безье
- •13.3.2. Свойства обобщенных полиномов бернштейна
- •14. Особенности аппроксимации обводов параметрическими полиномами в форме бернштейна
- •14.1. Методы полиномиальной аппроксимации одномерных обводов
- •14.1.1. Общая постановка задачи аппроксимации дискретного набора данных
- •14.1.2. Аппроксимация обводов параметрическими полиномами
- •14.1.3. Аппроксимация обводов параметрическими полиномами бернштейна
- •14.2. Геометрические свойства производных полиномов бернштейна
- •14.2.1. Вычисление первой производной
- •14.2.2. Вычисление производных высшего порядка
- •14.3. Методы полиномиальной аппроксимации двумерных обводов
- •Метод тензорного произведения
- •Каркасный метод
- •14.3.3. Метод булевой суммы (поверхности Кунса)
- •15. Стандарты в графических системах сапр и современные растровые графические файлы
- •15.1. Графические системы класса 2d
- •15.2. Графические системы класса 3d
- •15.3. Стандарты обмена данными
- •16. Системы подготовки и выпуска конструкторско-технологической документации. Организация конструкторской подготовки производства
- •17. Графические диалоговые системы
- •17.1. Краткий обзор зарубежных cad-систем
- •Технологические модули в pt/Products. Интеграция процессов проектирования и изготовления
- •Работа со стандартными библиотеками посредством pt/LibraryAccess и pt/Library
- •17.2. Отечественные разработки
- •Компас 5
- •T-flex cad
- •Заключение
- •394026 Воронеж, Московский просп., 14
13.2.2. Анализ алгоритма кастельжо для произвольной кривой
Приведенные выражения для квадратичной
параболы легко обобщаются на случай
произвольной пространственной кривой
![]() -го
порядка.
-го
порядка.
Пусть
![]() -
произвольные точки в пространстве
-
произвольные точки в пространстве![]() ,
,![]() .
Тогда для параболы
.
Тогда для параболы![]() -го
порядка запишем
-го
порядка запишем
|
|
( 8 ) |
Отметим, что
![]() .
Значение
.
Значение![]() определяет
точку со значением параметра
определяет
точку со значением параметра![]() на
кривой Безье
на
кривой Безье![]() .
.
Ломаная
![]() ,
образованная отрезками прямых, соединяющих
точки
,
образованная отрезками прямых, соединяющих
точки![]() ,
называется ломаной Безье, или управляющей
ломаной кривой
,
называется ломаной Безье, или управляющей
ломаной кривой![]() .
Соответственно, вершины ломаной
.
Соответственно, вершины ломаной![]() называются
управляющими точками, или точками
Безье.
На рис. 6 показано определение
точки на кубической кривой Безье с
помощью алгоритма Кастельжо.
называются
управляющими точками, или точками
Безье.
На рис. 6 показано определение
точки на кубической кривой Безье с
помощью алгоритма Кастельжо.

Рис. 13.6. Построение
точки
![]() на
кубической кривой с использованием
повторяющейся линейной интерполяции
на
кубической кривой с использованием
повторяющейся линейной интерполяции
Промежуточные
точки
![]() удобно
записывать, используя схему Кастельжо,
т.е. в виде треугольного массива.
Например, для кубической кривой схема
Кастельжо выглядит следующим образом:
удобно
записывать, используя схему Кастельжо,
т.е. в виде треугольного массива.
Например, для кубической кривой схема
Кастельжо выглядит следующим образом:
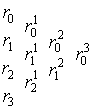
Произвольную
точку кривой
![]() также
можно вычислить с помощью полиномов
Бернштейна:
также
можно вычислить с помощью полиномов
Бернштейна:
|
|
( 9 ) |
Важно, что в случае
![]() это
уравнение дает точку на кривой:
это
уравнение дает точку на кривой:
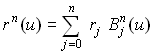 .
.
13.2.3. Обобщённый алгоритм для треугольной порции поверхности
Для определения точки, инцидентной
треугольной порции поверхности, с
заданными барицентрическими координатами
используем обобщение линейной интерполяции
для произвольной кривой
![]() -го
порядка.
-го
порядка.
Дано:характеристический многогранник
треугольной порции поверхности![]() и
точка в пространстве
и
точка в пространстве![]() ,
заданная барицентрическими координатами
,
заданная барицентрическими координатами![]() .
.
Найти:точку, инцидентную заданной порции поверхности, с соответствующими барицентрическими координатами.
Алгоритм
Для треугольной порции
поверхности, ограниченной кривыми
![]() -го
порядка, число точек характеристического
многогранника (управляющих точек)
вычисляется по формуле:
-го
порядка, число точек характеристического
многогранника (управляющих точек)
вычисляется по формуле:
![]() .
.
Введем некоторые обозначения:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Произвольная
точка с барицентрическими координатами
![]() ,
инцидентная заданной порции поверхности,
определяется с помощью повторяющейся
линейной интерполяции каждых трех точек
характеристического многогранника:
,
инцидентная заданной порции поверхности,
определяется с помощью повторяющейся
линейной интерполяции каждых трех точек
характеристического многогранника:
|
|
(10) |
где
![]() ,
,![]() .
.
Последний шаг
алгоритма дает искомую точку
![]() .
.
Граничные кривые треугольной порции определяются соответствующими характеристическими ломаными. Одна из барицентрических координат произвольной точки на этих кривых равна 0. Подставим в уравнение (10) барицентрические координаты границ треугольной области:
![]() ,
,![]() ,
,![]() .
.
Получим уравнения для определения точек на граничных кривых порции поверхности:
![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() ,
,![]() .
.
Сравнивая любое из полученных уравнений с уравнением (8), убеждаемся, что они эквивалентны. Следовательно, можно сделать вывод о том, что алгоритм, описываемый уравнением (10), является обобщением алгоритма для одномерного случая (8).
Пример Рассмотрим алгоритм для треугольной порции, ограниченной кубическими кривыми Безье.
Характеристический многогранник такой порции содержит 10 управляющих точек (рис. 13.7.):
![]() .
.
Сумма всех индексов каждой управляющей точки равна 3:
![]() ,
,![]() ,
,![]() .
.
Подставляем эти значения в формулу (10). На рис. 9 показано формирование треугольных массивов управляющих точек на каждом шаге алгоритма. На рис. 9 иллюстрируется повторяющаяся линейная интерполяция трех точек. На последнем шаге алгоритма вычисляется радиус-вектор точки с заданными барицентрическими координатами, инцидентной треугольной кубической порции поверхности.

Рис. 13.7. Характеристический многогранник кубической треугольной порции поверхности
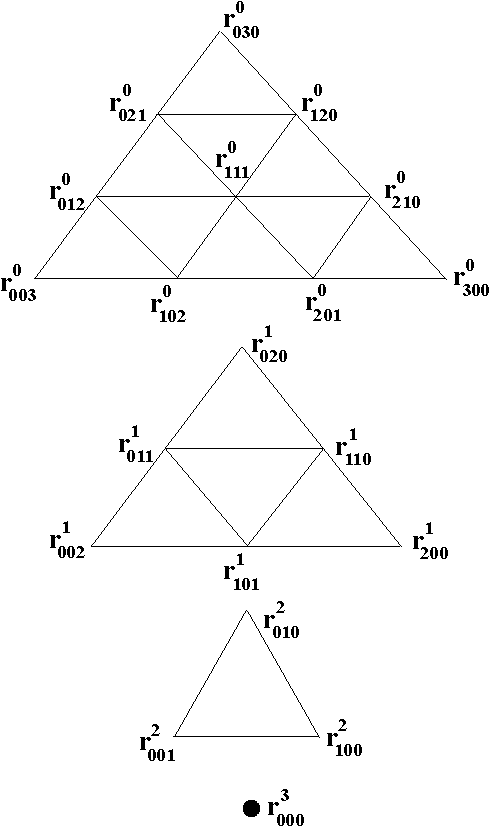
Рис. 13.8. Формирование треугольных массивов управляющих точек

Рис. 13.9. Иллюстрация работы алгоритма для треугольной кубической порции поверхности