13.1.3. Барицентрические координаты в пространстве

Метод барицентрических координат можно обобщить и на пространства высших размерностей. Например, в трехмерном пространстве барицентрические координаты точки относительно базового тетраэдраможно выразить через объемысоответствующих тетраэдров,,,,с помощью уравнений:

.

( 6 )

Уравнения ( 6 ) справедливы, если точка лежит внутри тетраэдра. Если же точкаявляется произвольной точкой пространства, то уравнения ( 6 ) останутся справедливыми, если подпонимать ориентированные объемы соответствующих тетраэдров.

13.2. Метод определения точек, инцидентных треугольной порции поверхности, по заданным локальным координатам

В алгоритме определения точки, инцидентной треугольной порции поверхности, используем рассмотренный нами выше метод барицентрических координат и связанную с ним линейную интерполяцию трех точек. Для этого обобщим алгоритм построения точки на кривой с заданным значением параметра, известный как алгоритм Кастельжо.

Алгоритм Кастельжо является одним из фундаментальных в области математического описания криволинейных поверхностей и имеет простую, интуитивно понятную геометрическую интерпретацию. Впервые основы алгоритма были опубликованы в технических отчетах фирмы Ситроен.

13.2.1. Алгоритм задания квадратичной параболы

Рассмотрим простую схему конструирования квадратичной параболы, которую далее обобщим для кривых Безье произвольного порядка. Пусть - три произвольные точки в пространстве, и пусть. Запишем следующие выражения:

.

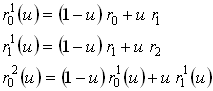Подставляя первые два уравнения в третье, получим уравнение второго порядка относительно переменной :

(7)

Таким образом, при изменении переменной отдоуравнение ( 7 ) описывает параболу, которую мы будем обозначать. Приведенные выше выражения представляют собой повторяющуюся линейную интерполяцию, иллюстрация которой приведена на рис. 4. При значениях переменной в интервале от 0 до 1 параболалежит внутри треугольника, образованного точками. В частности, отметим, что

.

Анализируя расположение точек на рис. 13.4, можно отметить равенство отношений

.

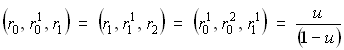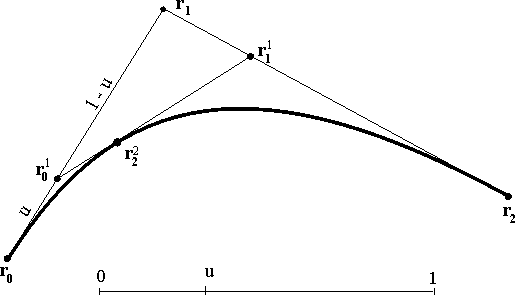
Рис. 13.4. Конструирование параболы с использованием линейной интерполяции

Так как кусочная линейная интерполяция аффинно инвариантна, то сконструированная парабола обладает таким же свойством. Можно также отметить, что данная кривая является плоским коническим сечением, поскольку любая точка на ней однозначно определяется заданием трех барицентрических координат.

Прежде чем рассмотреть алгоритм Кастельжо для произвольной кривой, приведем теорему о трех касательных, полностью связанную с вышеприведенным конструированием параболы. Пусть - три действительные различные точки на параболе (рис. 13.5).

Рис. 13.5. Иллюстрация теоремы о трех касательных

Проведем касательные к параболе в этих точках. Обозначим точки пересечения касательных.

Тогда справедливо равенство отношений .

Эта теорема определяет свойства квадратичной параболы. Теперь, учитывая конструктивные аналогии, рассмотрим алгоритм линейной интерполяции для произвольной кривой.