Вопрос 27. Формула Тейлора. Остаточный член в форме Лагранжа
Теорема 2.2. Если в некоторой окрестности точки х = а функция имеет конечные производные до (n+1)-го порядка включительно, то для любой точки этой окрестности справедлива формула
,
где
.
.
Данное
выражение для
называется остаточным членом в форме
Лагранжа.
Если
представить
в виде
,
где
,
то остаточный член примет вид
.
В
частном случае, если
,
,
то формула Тейлора примет вид
При
n
= 0 из формулы Тейлора получается формула
теоремы Лагранжа о конечном приращении
функции
Найдем
,
т.
е. остаточный член
является бесконечно малой функцией по
сравнению с
.
Поэтому его можно кратко записать
следующим образом
.
Данная запись остаточного члена называется в форме Пеано.
Вопрос 28. Формула Маклорена
Если а = 0, то формула Тейлора принимает вид
,
где .
Данный
вид формулы называется формулой
Маклорена. В этом случае остаточный
член (последнее слагаемое в формуле) в
форме Лагранжа имеет вид
,
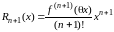а в форме Пеано
.
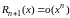Разложение основных элементарных функций по формуле Маклорена
Найдем
производные функций и их значения
в начале координат (при х
= 0), запишем разложения следующих функций:
.
1.
.
.
2. |
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
||||||
3. |
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
||||||
4. |
|
|
. |
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
||||||
.
.
.
2.4.4. Применение формулы Маклорена для вычисления пределов и значений функций
Пример
2.18.
Найти предел
.
Используя
формулу Маклорена, разложим по степеням
х
функции
и cosx.
В разложениях возьмем столько слагаемых,
чтобы остаточные члены (они записаны в
форме Пеано) были более высокого порядка
малости, чем бесконечно малая функция
,
стоящая в знаменателе. Выполним приведение
подобных. Учтем, что сумма (разность)
бесконечно малых функций
и
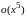является
.
Получим
.
Пример
2.20. Вычислить
число е
с точностью
.
Запишем
разложение функции
по
степеням х
,
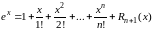где
,
.
При
х
= 1 получим
.
Пусть
нам известно, что это число меньше трех
(e
<3), поэтому можно записать
.
Найдем оценку остаточного члена при
различных значениях n,
равных 1, 2, 3, 4, 5, 6. Получим
n
= 1,
;
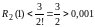n
= 2,
;
n
= 3,
;
n
= 4,
;
n
= 5,
;
n
= 6,
.
Следовательно, для того, чтобы вычислить значение числа е с точностью , необходимо учесть в разложении по формуле Маклорена 6 слагаемых. Находим
.
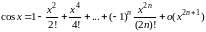
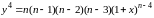