
- •Вопрос 1. Определение множества
- •1.1.2. Операции над множествами
- •1.1.3. Свойства операций над множествами
- •1.2. Функции, их классификация
- •1.3. Предел последовательности
- •Вопрос4
- •Односторонние пределы. Необходимое и достаточное условия существования предела функции
- •Вопрос 6. Бесконечно малые и бесконечно большие функции
- •Вопрос 7. Теоремы о представлении функции в виде суммы предела и бесконечно малой функции
- •Вопрос8 Первый замечательный предел
- •Вопрос 9. Второй замечательный предел
- •1.8.3. Применение второго замечательного предела в финансовых вычислениях
- •Вопрос 10.Сравнение бесконечно малых функций
- •Вопрос 11.Непрерывность функции в точке и на отрезке.
- •Вопрос 12.Свойства непрерывных функций
- •Вопрос 13.Точки разрыва функций
- •Вопрос14.Определение производной функции
- •Дифференцируемость функции, ее взаимосвязь с производной и непрерывностью функции
- •Вопрос 16.Вывод производных основных элементарных функций
- •Правила дифференцирования
- •2.1.9. Производные высших порядков
- •Вопрос 20. Эластичность функции
- •2.1.11. Геометрический смысл эластичности
- •2.2.2. Геометрический смысл дифференциала
- •2.2.3. Свойства дифференциала
- •Вопрос 22. Применение дифференциала для приближенных вычислений
- •Вопрос 23.Теоремы о дифференцируемых функциях
- •2.3.1. Теорема Ролля
- •2.3.2. Геометрический смысл теоремы Ролля
- •2.3.3. Примеры использования теоремы Ролля
- •24. Теорема Лагранжа о конечном приращении функции
- •2.3.5. Геометрический смысл теоремы Лагранжа
- •2.3.6. Теорема Коши
- •2.3.7. Раскрытие неопределенностей при нахождении пределов. Правило Лопиталя
- •Вопрос 27. Формула Тейлора. Остаточный член в форме Лагранжа
- •Вопрос 28. Формула Маклорена
- •2.4.4. Применение формулы Маклорена для вычисления пределов и значений функций
- •2.5. Исследование функций
- •2.5.1. Необходимый и достаточный признаки монотонности функций
- •Вопрос 31. Определение экстремума функции
- •Вопрос 32.Первый достаточный признак экстремума функции (с использованием первой производной)
- •34. Необходимый признак существования точки перегиба
- •35.Асимптоты графика функции
- •2.5.11. Построение графика функции
- •3.4. Свойства пределов
- •38.Бесконечно малые функции нескольких переменных
- •47. . Производная функции по направлению
2.5. Исследование функций
2.5.1. Необходимый и достаточный признаки монотонности функций
Функция
называется монотонно возрастающей
(рис.29) (убывающей (рис.30)) на интервале
(a,
b),
если
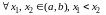
 ,
(
,
(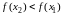 ).
).
Теорема 2.3. Необходимый признак монотонности функции. Если функция монотонно возрастает (убывает) на интервале (a, b), то ее производная в любой точке этого интервала неотрицательная (неположительная).
Теорема
2.4. Достаточный
признак монотонности функции. Если на
интервале (a,
b)
для любого значения х
производная функции положительная
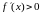 (отрицательная
(отрицательная
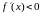 ),
то функция монотонно возрастает
(убывает).
),
то функция монотонно возрастает
(убывает).
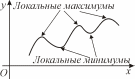
Вопрос 31. Определение экстремума функции
Рис. 31 |
Точка
называется точкой локального максимума
(минимума) функции
,
если существует некоторая окрестность
этой точки |
Максимум и минимум функции называются экстремумами.
Необходимый признак экстремума функции
Теорема 2.5. Если точка является точкой экстремума функции , то производная функции в этой точке либо равна нулю, либо не существует.
Вопрос 32.Первый достаточный признак экстремума функции (с использованием первой производной)
Теорема
2.6. Если в
окрестности критической точки
функция
является непрерывной, а так же
дифференцируемой в этой окрестности,
за исключением быть может самой точки,
и при переходе х
через
производная
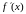 изменяет знак, то
является точкой локального экстремума;
причем, если знак
изменяется с «+» на «»,
то
точка максимума, если знак изменяется
с «»
на «+», то
точка минимума.
изменяет знак, то
является точкой локального экстремума;
причем, если знак
изменяется с «+» на «»,
то
точка максимума, если знак изменяется
с «»
на «+», то
точка минимума.
Второй достаточный признак экстремума функции
(с использованием производной второго порядка)
Теорема
2.7. Если
функция
является непрерывной и дважды
дифференцируемой в окрестности точки
,
производная функции в этой точке равна
нулю
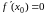 ,
а производная второго порядка отлична
от нуля
,
а производная второго порядка отлична
от нуля
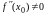 ,
то
является точкой локального экстремума
функции; причем, если
,
то
является точкой локального экстремума
функции; причем, если
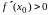 ,
то имеет место минимум, а если
,
то имеет место минимум, а если
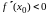
максимум.
максимум.
2.5.6. Определение выпуклости, вогнутости
графика функции, точки перегиба
Рис. 36 |
График функции называется выпуклым (вогнутым) вверх на некотором интервале, если он находится ниже (выше) касательной к графику функции, проведенной в любой точке этого интервала (рис. 36). |
33.Достаточный признак выпуклости, вогнутости графика функции
Теорема
2.8. Если
функция
является непрерывной и дважды
дифференцируемой на интервале
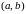 и производная второго порядка в любой
точке этого интервала положительная
и производная второго порядка в любой
точке этого интервала положительная
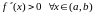 (отрицательная
(отрицательная
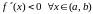 ),
то график функции является вогнутым
(выпуклым)
),
то график функции является вогнутым
(выпуклым)
на этом интервале.
34. Необходимый признак существования точки перегиба
Теорема
2.9. Если точка
является точкой перегиба графика функции
,
то производная функции второго порядка
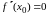 в этой точке либо равна нулю, либо не
существует.
в этой точке либо равна нулю, либо не
существует.
Точки,
в которых
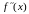 либо равняется нулю, либо не существует,
называются критическими для производной
второго порядка.
либо равняется нулю, либо не существует,
называются критическими для производной
второго порядка.
Достаточный признак существования точки перегиба
Теорема
2.10. Если в
окрестности критической точки
функция
является непрерывной, а так же дважды
дифференцируемой в этой окрестности,
за исключением быть может самой точки,
и при переходе х
через
производная второго порядка изменяет знак, то
является точкой перегиба.
изменяет знак, то
является точкой перегиба.

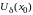 ,
что для любой точки этой окрестности
,
что для любой точки этой окрестности
 (
(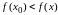 )
(Рис. 31).
)
(Рис. 31).