1.3. Предел последовательности

Окрестностью точки называется любой интервал, содержащий эту точку.

-окрестностью точки называется интервал длиной 2 с центром в этой точке.

Определение предела последовательности. Число b называется пределом последовательности ( ), если для любого, сколь угодно малого, положительного  существует такое положительное число N, что если номер члена последовательности n > N, то принадлежит -окрестности числа b (  ).

Теорема Больцано-Коши Для того, чтобы последовательность имела предел, необходимо и достаточно, чтобы для любого  > 0 существовало N()> 0 такое, что если n > N, m > N, то .

Теорема Вейерштрасса Если последовательность монотонно возрастает (убывает) и ограничена сверху (снизу), то она имеет предел.

Последовательность называется монотонно возрастающей (убывающей), если для любого n  N ( ).

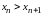Определение предела функции по Гейне. Число b называется пределом функции при ( ), если любой последовательности , ( ), стремящейся к , соответствует последовательность значений функции , стремящаяся к b.

Определение предела функции по Коши (на языке ). Число b называется пределом функции при ( ), если для любого положительного числа  существует такое положительное число , зависящее от , что если значение х принадлежит -окрестности числа , то значение функции принадлежит -окрестности числа b.

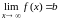Определение предела функции по Коши при . Число b называется пределом функции при ( ), если для любого положительного числа  существует такое положительное число N, зависящее от , что если значение > N, то значение функции принадлежит -окрестности числа b ( ).

Вопрос4

Геометрический смысл предела

изображены окрестности и в случае предела

.

для случая предела изображена -окрестность числа b и такое число N(), что если x > N(), то соответствующие значения функции попадают в -окрестность числа b и не покидают ее никогда.

Односторонние пределы. Необходимое и достаточное условия существования предела функции

	 называется правосторонним пределом функции f(x) в точке или пределом справа.
	 называется левосторонним пределом функции f(x) в точке или пределом слева.

Теорема 1.1. Для того, чтобы существовал предел функции , необходимо и достаточно чтобы существовали односторонние пределы функции равные между собой, т. е.

Вопрос 6. Бесконечно малые и бесконечно большие функции

Определение бесконечно малой функции. Функция (x) называется бесконечно малой функцией при , если для любого сколь угодно малого положительного числа  существует такое положительное число , зависящее от , что для любого x, принадлежащего -окрестности (x) находится в -окрестности начала координат (x) , т.е. .

Определение бесконечно большой функции. Функция называется бесконечно большой при , если для любого сколь угодно большого положительного числа N существует такое положительное число , зависящее от N, что если x принадлежит -окрестности числа ( ), то абсолютная величина значения функции больше числа N ( ), т.е. .

Теорема 1.2. Функция, обратная по величине к бесконечно малой функции является бесконечно большой и, наоборот, функция, обратная по величине к бесконечно большой, является бесконечно малой функцией.

Свойства бесконечно малых функций

Свойство 1. Сумма конечного числа бесконечно малых функций является бесконечно малой функцией.

Свойство 2. Произведение бесконечно малой функции на ограниченную функцию является бесконечно малой функцией.

Следствие 1. Произведение бесконечно малой функции на постоянную величину С является бесконечно малой функцией, т. е. .

Следствие 2. Произведение бесконечно малых функций и является бесконечно малой функцией.

Свойство 3. Частное от деления бесконечно малой функции на функцию , предел которой отличен от нуля ( ) является бесконечно малой функцией.