
- •Вопрос 1. Определение множества
- •1.1.2. Операции над множествами
- •1.1.3. Свойства операций над множествами
- •1.2. Функции, их классификация
- •1.3. Предел последовательности
- •Вопрос4
- •Односторонние пределы. Необходимое и достаточное условия существования предела функции
- •Вопрос 6. Бесконечно малые и бесконечно большие функции
- •Вопрос 7. Теоремы о представлении функции в виде суммы предела и бесконечно малой функции
- •Вопрос8 Первый замечательный предел
- •Вопрос 9. Второй замечательный предел
- •1.8.3. Применение второго замечательного предела в финансовых вычислениях
- •Вопрос 10.Сравнение бесконечно малых функций
- •Вопрос 11.Непрерывность функции в точке и на отрезке.
- •Вопрос 12.Свойства непрерывных функций
- •Вопрос 13.Точки разрыва функций
- •Вопрос14.Определение производной функции
- •Дифференцируемость функции, ее взаимосвязь с производной и непрерывностью функции
- •Вопрос 16.Вывод производных основных элементарных функций
- •Правила дифференцирования
- •2.1.9. Производные высших порядков
- •Вопрос 20. Эластичность функции
- •2.1.11. Геометрический смысл эластичности
- •2.2.2. Геометрический смысл дифференциала
- •2.2.3. Свойства дифференциала
- •Вопрос 22. Применение дифференциала для приближенных вычислений
- •Вопрос 23.Теоремы о дифференцируемых функциях
- •2.3.1. Теорема Ролля
- •2.3.2. Геометрический смысл теоремы Ролля
- •2.3.3. Примеры использования теоремы Ролля
- •24. Теорема Лагранжа о конечном приращении функции
- •2.3.5. Геометрический смысл теоремы Лагранжа
- •2.3.6. Теорема Коши
- •2.3.7. Раскрытие неопределенностей при нахождении пределов. Правило Лопиталя
- •Вопрос 27. Формула Тейлора. Остаточный член в форме Лагранжа
- •Вопрос 28. Формула Маклорена
- •2.4.4. Применение формулы Маклорена для вычисления пределов и значений функций
- •2.5. Исследование функций
- •2.5.1. Необходимый и достаточный признаки монотонности функций
- •Вопрос 31. Определение экстремума функции
- •Вопрос 32.Первый достаточный признак экстремума функции (с использованием первой производной)
- •34. Необходимый признак существования точки перегиба
- •35.Асимптоты графика функции
- •2.5.11. Построение графика функции
- •3.4. Свойства пределов
- •38.Бесконечно малые функции нескольких переменных
- •47. . Производная функции по направлению
3.4. Свойства пределов
Пределы функций нескольких переменных обладают такими же свойствами, как и пределы функций одной переменной.
Теорема
3.1. Если
функции
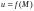 и
и
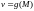 имеют одинаковые области определения
и имеют конечные пределы при
имеют одинаковые области определения
и имеют конечные пределы при
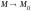
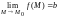 и
и
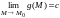 ,
где
b
= const, c
= const,
,
где
b
= const, c
= const,
то справедливы следующие соотношения:
1)
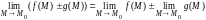 ;
;
2)
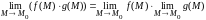 ;
;
3)
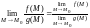 ,
если
,
если
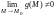 .
.
38.Бесконечно малые функции нескольких переменных
Функция
нескольких переменных
 называется бесконечно малой функцией
при
называется бесконечно малой функцией
при
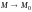 ,
если
,
если
 .
.
 .
.
Бесконечно малые функции нескольких переменных обладает такими же свойствами, что и бесконечно малые функции одной переменной.
Непрерывность функций нескольких переменных. Точки и линии разрыва
Опр.1.
Функция
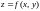 называется непрерывной в точке
называется непрерывной в точке
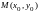 ,
если она определена в окрестности этой
точки и бесконечно малым приращениям
независимых переменных соответствует
бесконечно малое приращение функции,
т. е.
,
если она определена в окрестности этой
точки и бесконечно малым приращениям
независимых переменных соответствует
бесконечно малое приращение функции,
т. е.
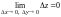 .Опр.
2. Функция
.Опр.
2. Функция
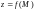 называется непрерывной в точке
называется непрерывной в точке
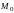 ,
если она определена в окрестности этой
точки и
,
если она определена в окрестности этой
точки и
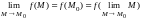 .
.
Можно записать с помощью кванторов на языке «».
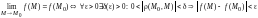
Точка
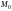 называется точкой разрыва функции
нескольких переменных, если функция не
является непрерывной в этой точке.Функции
нескольких переменных могут иметь линии
разрыва. Например,
называется точкой разрыва функции
нескольких переменных, если функция не
является непрерывной в этой точке.Функции
нескольких переменных могут иметь линии
разрыва. Например,
 имеет две линии разрыва в виде
пересекающихся прямых
имеет две линии разрыва в виде
пересекающихся прямых
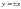 ;
а функция
;
а функция
 имеет линию разрыва в виде параболы
имеет линию разрыва в виде параболы
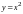 .
.
Свойства непрерывных функций
1. Если функция нескольких переменных является непрерывной в замк-нутой области, то она достигает в этой области своего наибольшего и наи-меньшего значений.
2. Если функция нескольких переменных является непрерывной в замк-нутой области, то она хотя бы один раз принимает в этой области любое значение между своим наименьшим и наибольшим значениями.
3. Если функция непрерывна в замкнутой области, то она равномерно-непрерывная в этой области.
39..Частные приращения и частные производные функции нескольких переменных
Для
функции
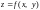 частными приращениями по х
и по y
называется соответственно
частными приращениями по х
и по y
называется соответственно
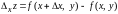 ,
,
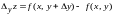 .
.
Частной производной функции нескольких переменных по некоторой переменной называется предел отношения частного приращения функции по этой переменной к приращению переменной, стремящемуся к нулю, т. е.
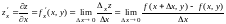 ,
,
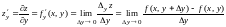 .
.
Правило нахождения частных производных функций нескольких переменных. Для того чтобы найти частную производную функции нескольких переменных по некоторой переменной, необходимо все независимые переменные функции кроме данной считать постоянными и найти производную как от функции одной переменной.
Геометрический смысл частных производных
Пусть
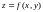 ,
,
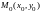 ,
,
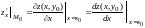 .
.
40. Необходимые условия дифференцируемости функции нескольких переменных |
Частная
производная функции
|
Функция
 называется дифференцируемой
в точке
называется дифференцируемой
в точке
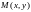 ,
если ее полное приращение в этой точке
может быть представлено в виде
,
если ее полное приращение в этой точке
может быть представлено в виде
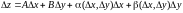 ,
,
1.Если функция нескольких переменных,дифференцируемая внекоторой точке,она непрерывна в этой точке.
Д
о к-во По определению, функция является
непрерывной, если
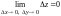 .
Найдем
.
Найдем
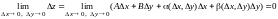 .
.
2.Если функция нескольких переменных,дифференцируемая в точке,она имеет частные производные в этой точке.
Д
о к-во Пусть
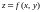 дифференцируемая. Если y
= const,
то y
= 0. Тогда
дифференцируемая. Если y
= const,
то y
= 0. Тогда
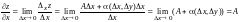 .
.
Если x = const, то x = 0. Тогда
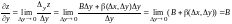 .
.
Пример1. Функция непрерывна в точке О(0,0)., от противного
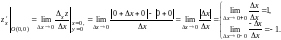
Следовательно,
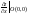 не существует. Аналогично получаем, что
не существует. Аналогично получаем, что
 также не существует.
также не существует.
Пример2.
функция
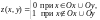 имеет
частные производные в точке O(0,
0), но не является дифференцируемой.
имеет
частные производные в точке O(0,
0), но не является дифференцируемой.
Находим
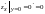 ,
,
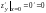 .
.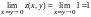 ,
но
,
но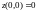 ,
не равно 1. Функция не является непрерывной,
а следовательно не является дифференцируемой.
,
не равно 1. Функция не является непрерывной,
а следовательно не является дифференцируемой.
Пример3.
что функция
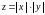 является не дифференцируемой. непрерывна
в точке O(0,
0), так как
является не дифференцируемой. непрерывна
в точке O(0,
0), так как
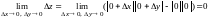 .
.
Также эта функция имеет частные производные в точке O(0, 0):
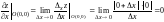 .
.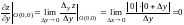
Однако,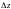 функции
функции
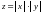 невозможно
представить в виде
невозможно
представить в виде
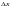 и
и
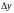 ,функция
не дифференцируемая
,функция
не дифференцируемая
41. Достаточные условия дифференцируемости функции нескольких переменных
Для
того, чтобы функция
была дифференцируемой в точке М
(x,
y),
она должна быть непрерывной и иметь
непрерывные частные производные в этой
точке.Д о к а з а т е л ь с т в о. Запишем
полное приращение функции
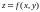
 .
.
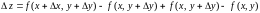 .Тогда
.Тогда
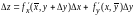 (
По теореме Лагранжа о конечном приращении)
(
По теореме Лагранжа о конечном приращении)
Так как частные производные по условию теоремы непрерывны, то
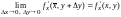 ,
,
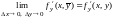 .
.
Используя теорему 1.3 о представлении функции в виде суммы предела и бесконечно малой функции, запишем
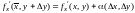 ,
,
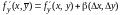 ,
,
 -
является дифф.
-
является дифф.
Следствие. Для того, чтобы установить дифференцируемость функции, нужно проверить непрерывность частных производных.
42. Полный дифференциал функции нескольких переменных
Сумма первых двух слагаемых в выражении полного приращения z называется полным дифференциалом и записывается
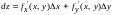 .
.
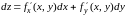
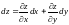 .Полное
приращение функции
.Полное
приращение функции
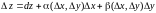 .
.
Найдем
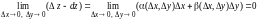 ,
,
Определение полного дифференциала функции нескольких переменных. Полным дифференциалом функции нескольких переменных называется бесконечно малая функция прямо пропорциональная бесконечно малым приращениям независимых переменных и отличающаяся от полного приращения функции на бесконечно малую функцию более высокого порядка малости по сравнению бесконечно малыми приращениями независимых переменных.
43. Применение полного дифференциала функции нескольких переменных для приближенных вычислений
1. Вычисление значений функций и их приращений.
Используем
то, что полный дифференциал является
главной линейной частью приращения
функции (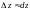 ).
Пусть известно значение функции
).
Пусть известно значение функции
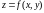 в некоторой точке
в некоторой точке
 и имеется точка
и имеется точка
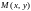 ,
находящейся в некоторой достаточно
малой окрестности точки
,
находящейся в некоторой достаточно
малой окрестности точки
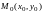 .
.
приращение
функции
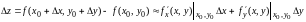 .
.
значение
этой функции
 .
.
2. Оценка погрешности вычислений значений функций.
функция
зависит от n
переменных
 .
Тогда
.
Тогда
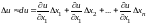 .
.
Абсолютная
погрешность
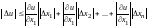 или
или
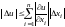 .
.
44.
Частные
производные высших порядков Частной
производной n-го
порядка называется частная производная
от частной производной (n1)-го
порядка. Например, пусть функция
 зависит от двух переменных. Она имеет
две частные производные
зависит от двух переменных. Она имеет
две частные производные
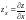 и
и
 .
Каждую из этих производных в свою
очередь можно продифференцировать по
каждой из независимых переменных и
получить четыре производные второго
порядка:
.
Каждую из этих производных в свою
очередь можно продифференцировать по
каждой из независимых переменных и
получить четыре производные второго
порядка:
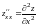 ,
,
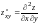 ,
,
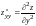 и
и
 .
Теорема 3.5.
Смешенные частные производные не зависят
от порядка дифференцирования, если они
являются непрерывными.
.
Теорема 3.5.
Смешенные частные производные не зависят
от порядка дифференцирования, если они
являются непрерывными.
Дифференциалы высших порядков.Дифференциалом n-го порядка называется дифференциал от дифференциала (n1)-го порядка, полученный в предположении, что дифференциалы независимых переменных постоянны.
Полный
дифференциал функция
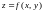 равен
равен
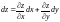 .
.
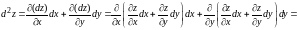
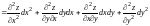 .
.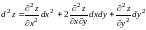 .
.
Дифференциал
k-го
порядка
 имеет вид
имеет вид .
.
45. Частные производные сложной функции нескольких переменных
Функция
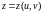 называется сложной, если ее аргументы
являются в свою очередь функциями
каких-либо других переменных, например,
называется сложной, если ее аргументы
являются в свою очередь функциями
каких-либо других переменных, например,
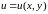 ,
,
 .
.
Пусть
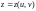 ,
,
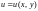 и
и
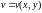 являются непрерывными и
дифференцируемыми.y=const
являются непрерывными и
дифференцируемыми.y=const
 ,
,
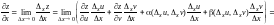
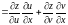 .
Аналогично, в случае, х
= const,
а y
получает приращение y
.
Аналогично, в случае, х
= const,
а y
получает приращение y
В
случае сложной функции ;
;
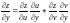 .
.
когда
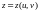 ,
,
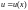 ,
,
 ,
,
 ;
;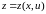 ,
,
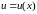 ,
то
,
то
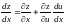 .
.
46.
. Производная
функции, заданной неявно.Функция
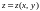 называется заданной неявно, если она
задана уравнением
называется заданной неявно, если она
задана уравнением
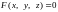 неразрешенным относительно z.
неразрешенным относительно z.
 геометрически
представляет поверхность в трехмерном
пространстве. Пусть на этой поверхности
имеются две точки
геометрически
представляет поверхность в трехмерном
пространстве. Пусть на этой поверхности
имеются две точки
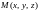 и
и
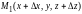 .
.
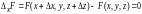 .Пусть
.Пусть
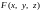 является дифф.,тогда
является дифф.,тогда
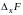
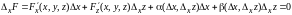 ,
,
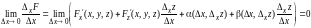
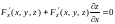 .
Сл-но
.
Сл-но .
.
 .-(по
у)
.-(по
у)
формулы
для нахождения частных производных
функции
 ,
заданной неявно,
,
заданной неявно,
 Неявная
функция 1 переменной задается уравнением
Неявная
функция 1 переменной задается уравнением
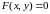 .
.
 .
.


 по x
в точке
по x
в точке
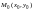 равняется тангенсу угла наклона
касательной, проведенной к линии,
образованной пересечением поверхности
равняется тангенсу угла наклона
касательной, проведенной к линии,
образованной пересечением поверхности
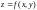 плоскостью
плоскостью
 в точке
в точке