- •Вопрос 1. Определение множества
- •1.1.2. Операции над множествами
- •1.1.3. Свойства операций над множествами
- •1.2. Функции, их классификация
- •1.3. Предел последовательности
- •Вопрос4
- •Односторонние пределы. Необходимое и достаточное условия существования предела функции
- •Вопрос 6. Бесконечно малые и бесконечно большие функции
- •Вопрос 7. Теоремы о представлении функции в виде суммы предела и бесконечно малой функции
- •Вопрос8 Первый замечательный предел
- •Вопрос 9. Второй замечательный предел
- •1.8.3. Применение второго замечательного предела в финансовых вычислениях
- •Вопрос 10.Сравнение бесконечно малых функций
- •Вопрос 11.Непрерывность функции в точке и на отрезке.
- •Вопрос 12.Свойства непрерывных функций
- •Вопрос 13.Точки разрыва функций
- •Вопрос14.Определение производной функции
- •Дифференцируемость функции, ее взаимосвязь с производной и непрерывностью функции
- •Вопрос 16.Вывод производных основных элементарных функций
- •Правила дифференцирования
- •2.1.9. Производные высших порядков
- •Вопрос 20. Эластичность функции
- •2.1.11. Геометрический смысл эластичности
- •2.2.2. Геометрический смысл дифференциала
- •2.2.3. Свойства дифференциала
- •Вопрос 22. Применение дифференциала для приближенных вычислений
- •Вопрос 23.Теоремы о дифференцируемых функциях
- •2.3.1. Теорема Ролля
- •2.3.2. Геометрический смысл теоремы Ролля
- •2.3.3. Примеры использования теоремы Ролля
- •24. Теорема Лагранжа о конечном приращении функции
- •2.3.5. Геометрический смысл теоремы Лагранжа
- •2.3.6. Теорема Коши
- •2.3.7. Раскрытие неопределенностей при нахождении пределов. Правило Лопиталя
- •Вопрос 27. Формула Тейлора. Остаточный член в форме Лагранжа
- •Вопрос 28. Формула Маклорена
- •2.4.4. Применение формулы Маклорена для вычисления пределов и значений функций
- •2.5. Исследование функций
- •2.5.1. Необходимый и достаточный признаки монотонности функций
- •Вопрос 31. Определение экстремума функции
- •Вопрос 32.Первый достаточный признак экстремума функции (с использованием первой производной)
- •34. Необходимый признак существования точки перегиба
- •35.Асимптоты графика функции
- •2.5.11. Построение графика функции
- •3.4. Свойства пределов
- •38.Бесконечно малые функции нескольких переменных
- •47. . Производная функции по направлению
2.2.2. Геометрический смысл дифференциала
Как
показано выше, для приращения функции
y
и ее дифференциала справедливо
приближенное равенство
 ,
где
угол наклона касательной к оси Ох.
Дифференциал функции dy
и ее приращение y
изображены на рис. 21, рис. 22.
,
где
угол наклона касательной к оси Ох.
Дифференциал функции dy
и ее приращение y
изображены на рис. 21, рис. 22.
Рис. 21 |
Рис. 22 |
Дифференциал
функции y
= f(x)
в точке
при приращении независимой переменной
x
равен
приращению ординаты
 касательной (
касательной (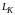 )
к графику функции в этой точке.
)
к графику функции в этой точке.
В зависимости от характера изменения функции дифференциал может быть больше (рис.21) или меньше (рис.22) приращения функции y.
2.2.3. Свойства дифференциала
Пусть u = u (x), v = v(x) дифференцируемые функции.
1.
 .
.
2.
 .
.
3.
 .
.
4. Вид дифференциала не зависит от того, является ли аргумент функции независимой переменной или в свою очередь является дифференцируемой функцией другой переменной.
Действительно,
если
,
то
 .
.
Если
,
,
то
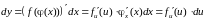 .
.
Вопрос 22. Применение дифференциала для приближенных вычислений
Вычисление приближенного значения функции или ее приращения.
Пусть
дифференцируемая функция в окрестности
точки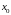 .
Тогда при бесконечно малом приращении
х
с точностью до бесконечно малой более
высокого порядка по сравнению с х
можно считать, что приращение
функции
.
Тогда при бесконечно малом приращении
х
с точностью до бесконечно малой более
высокого порядка по сравнению с х
можно считать, что приращение
функции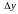 равняется
ее дифференциалу
равняется
ее дифференциалу
 ,
т. е.
,
т. е.
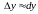 .
Данное приближенное равенство используют
для вычисления приращений функций и ее
значений по формулам
.
Данное приближенное равенство используют
для вычисления приращений функций и ее
значений по формулам
 ,
,
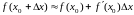 .
.
Пример
2.7. Вычислить
значение
 ,
используя дифференциал.
,
используя дифференциал.
Данный
корень является значением функции
 при х
= 10. Находим точку
= 8, которая является наиболее близкой
к х
= 10 и в которой значение данной функции
известно
при х
= 10. Находим точку
= 8, которая является наиболее близкой
к х
= 10 и в которой значение данной функции
известно .
Вычисляем величину приращения независимой
переменной х
= х
= 10
8 = 2. Находим производную функции
.
Вычисляем величину приращения независимой
переменной х
= х
= 10
8 = 2. Находим производную функции
 и ее значение в точке
и ее значение в точке
=
8,
 .
Вычисляем
.
Вычисляем
 .
.
Дифференциалы высших порядков
Дифференциалом n-го порядка называется дифференциал от дифференциала (n 1)-го порядка, полученный в предположении, что дифференциал независимой переменной постоянный, т. е.
 .
.
Находим
 ,
,
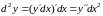 .
Очевидно,
.
Очевидно,
 .
.
Из
последнего равенства можно записать
 .
.
Вопрос 23.Теоремы о дифференцируемых функциях
2.3.1. Теорема Ролля
Теорема
Ролля. Если
функция y
= f(x)
непрерывна на отрезке [a,
b],
дифференцируемая в каждой его внутренней
точке и принимает равные значения в
граничных точках отрезка, то найдётся
такая внутренняя точка отрезка х=
с,
в которой производная функции равна
нулю

2.3.2. Геометрический смысл теоремы Ролля
Рис. 23
|
Если график функции y = f(x) непрерывный на отрезке [a, b] и гладкий (не имеет точек излома) на интервале (a, b) и ординаты графика функции в граничных точках отрезка равные f(а)= f(b), то найдется такая внутренняя точка отрезка х = с, в которой касательная параллельна оси Ох (рис. 23).
|