70.(30).Вы

числение длины дуги плоской кривой

3.1 Если функция y = f(x) непрерывна вместе с её производной f'(x) на отрезке [a, b], то длина дуги AB, где A(a,f(a)), B(b, f(b)), выражается формулой

                                    

3.2. Если кривая задана параметрическими уравнениями    , где x(t), y(t) - дифференцируемые функции, то длина дуги  

3.3. Если дуга задана в полярных координатах  ,   , то длина дуги  

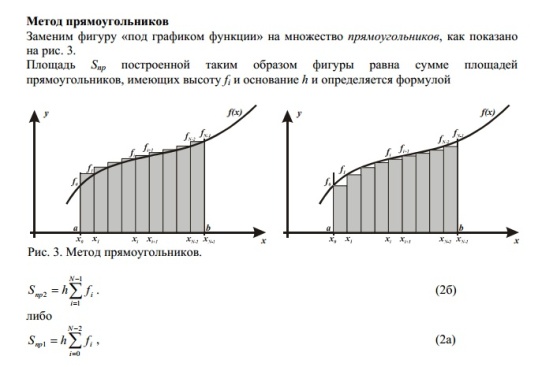
71.(55).Численные методы вычисления определенных интегралов. Методы прямоугольников и трапеций.

 

73-74.(42). Двойные интегралы. Их геометрический смысл. Свойства.

Двойные интегралы.Определение двойного интеграла, его свойства

Переходя к рассмотрению двойных интегралов для функции двух независимых переменных f (x, y), наиболее удобно для понимания начать с определения объема цилиндрического тела.

О п р е д е л е н и е. Цилиндрическим телом называется тело, ограниченное плоскостью хОу, поверхностью, с которой любая прямая, параллельная оси Oz, пересекается не более чем в одной точке, и цилиндрической поверхностью, образующая которой параллельна оси Oz.

Область D, высекаемая в плоскости хОу цилиндрической поверхностью, называется основанием цилиндрического тела (рис. 5).

Диаметром области называют наибольшее расстояние между точками ее границы.

В частных случаях боковая цилиндрическая поверхность может отсутствовать. Например, если тело ограничено плоскостью хОу и полусферой

  .

Обычно тело можно составить из некоторого числа цилиндрических тел и искомый объем определить как сумму объемов цилиндрических тел, составляющих этот объем.

Пусть Z = f (x, y) есть уравнение поверхности, ограничивающей цилиндрическое тело. Будем считать, что f(x, y) определена в ограниченной замкнутой области D плоскости хОу. Разобьем область D произвольным способом на n частичных областей с площадями   и диаметрами d₁,d₂,…,d_n. Выберем в каждой элементарной (частичной) области произвольную точку M_k(x_k, y_k) и умножим значение функции в точке M_k на площадь этой области.

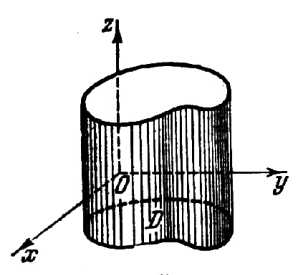И нтегральной суммой для функции Z = f (x, y) по области D называется сумма вида (n-я интегральная сумма)

. (87)

О п р е д е л е н и е. Двойным интегралом от функции f (x, y) по области D называется предел, к которому стремится n-я интегральная сумма при стремлении к нулю наибольшего диаметра частичных областей:

. (88)

При f (x, y) > 0, (поверхность Z = f (x, y) целиком лежит в верхней полуплоскости) двойной интеграл равен объему цилиндрического тела

, (89)

ограниченного областью D и поверхностью Z = f (x, y).

Т е о р е м а существования двойного интеграла.

Если функция f (x, y) непрерывна в области D, ограниченной замкнутой линией, то ее n-я интегральная сумма стремится к пределу при стремлении к нулю наибольшего диаметра частичных областей. Этот предел, т.е. двойной интеграл  , существует и не зависит от способа разбиения области D на частичные области и от выбора в них точек M_k.

Основные свойства двойных интегралов

1. Двойной интеграл от суммы конечного числа функций равен сумме двойных интегралов от слагаемых функций:

 (90)

2. Постоянный множитель подынтегральной функции можно вынести за символ двойного интеграла:

 (91)

3. Если область интегрирования разбита на две части D₁ и D₂, то

. (92)

4. Если во всех точках области D функции f (x, y) и   удовлетворяют условию  , то

. (93)

Знак неравенства может перейти в знак равенства только при совпадении функций.

С л е д с т в и е. Если подынтегральная функция в области интегрирования не меняет знака, то двойной интеграл есть число того же знака, что и функция.

5. Если функция f (x, y) во всех точках области интегрирования удовлетворяет неравенствам

,

то

, (94)

где S – площадь области D.

6. Двойной интеграл равен произведению значения подынтегральной функции в некоторой точке области интегрирования на площадь области интегрирования, т.е.

. (95)

Значение   из (95) называется средним значением функции f (x, y) в области D, а равенство (95) является, по существу, обобщением теоремы о среднем для определенного интеграла на двойной интеграл.