28. Замена переменных в тройном интеграле. Цилиндрические и сферические координаты.

Пусть исходный тройной интеграл задан в декартовых координатах x, y, z в области U: Требуется вычислить данный интеграл в новых координатах u, v, w. Взаимосвязь старых и новых координат описывается соотношениями:

Предполагается, что выполнены следующие условия:

1. Функции φ, ψ, χ непрерывны вместе со своими частными производными;

2. Существует взаимно-однозначное соответствие между точками области интегрирования U в пространстве xyz и точками области U' в пространстве uvw;

3. Якобиан преобразования I (u,v,w), равный

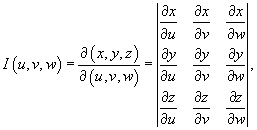
отличен от нуля и сохраняет постоянный знак всюду в области интегрирования U.

Тогда формула замены переменных в тройном интеграле записывается в виде:

В приведенном выражении   означает абсолютное значение якобиана. 

• 1) Если заданы сферические координаты точки, то переход к декартовым осуществляется по формулам;

• 2)Обратно, от декартовых к сферическим:

1)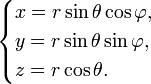 2)

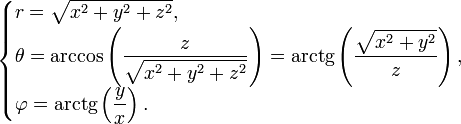
Якобиан преобразования от декартовых к сферическим:

1. Закон преобразования координат от цилиндрических к декартовым:

2. Закон преобразования координат от декартовых к цилиндрическим:

1)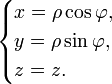 2) 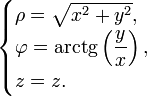Якобиан равен:

29. Вычисление площади гладкой поверхности, заданной параметрически и в явном виде.

Здесь  .

В координатах получаем:

	выражение для площади
явное задание
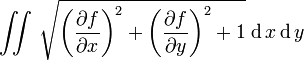
параметрическое задание

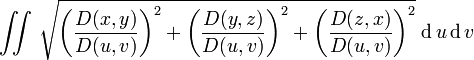
30(1). Определение криволинейных интегралов первого и второго рода, их основные свойства и вычисление.

 Криволинейный интеграл 1-го рода (Кри-1)         Сведение Кри-1 к определенному интегралу 

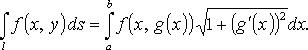     Если кривая l задана уравнением   то      Если кривая l задана параметрически   то 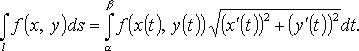     Криволинейный интеграл 2-го рода (Кри-2)         Изменение направления обхода по кривой 

     Сведение Кри-2 к определенному интегралу       1. Кривая l задана уравнением y = f(x), x изменяется от   до  :

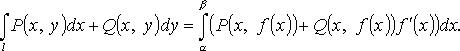
     2. Кривая l задана параметрически: x = x(t), y = y(t), t изменяется от   до  :

30(2). Определение криволинейных интегралов первого и второго рода, их основные свойства и вычисление.

Свойства криволинейного интеграла первого рода.

  1) Значение криволинейного интеграла по длине дуги не зависит от направления кривой АВ. 2) Постоянный множитель можно выносить за знак криволинейного интеграла. 3) Криволинейный интерал от суммы функций равен сумме криволинейных интегралов от этих функций. 4) Если кривая АВ разбита на дуга АС и СВ, то

 5) Если в точках кривой АВ  То

 6) Справедливо неравенство:

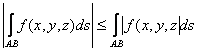
  7) Теорема о среднем.

  Если функция f(x, y, z) непрерывна на кривой АВ, то на этой кривой существует точка (x₁, y₁, z₁) такая, что

Свойства криволинейного интеграла второго рода

Криволинейный интеграл II рода обладает следующими свойствами:

1. Пусть C обозначает кривую с началом в точке A и конечной точкой B. Обозначим через −Cкривую противоположного направления - от B к A. Тогда

2. Если C − объединение кривых C₁ и C₂ (рисунок 2 выше), то

3. Если кривая C задана параметрически в виде 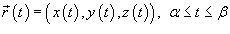 , то

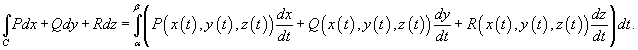
4. Если кривая C лежит в плоскости Oxy и задана уравнением   (предполагается, что R =0и t = x), то последняя формула записывается в виде