1. Определенный интеграл. Интегральная сумма. Верхняя и нижняя интегральные суммы. Их свойства.

2. Ограниченность интегрируемых функций.

3. Критерий интегрируемости ограниченной на отрезке функции.

4. Теорема об интегрируемости монотонной и непрерывной на отрезке функции.

5. Основные свойства определенного интеграла.

6. Формула среднего значения для определенного интеграла.

7. Интеграл с переменным верхним пределом. Его непрерывность и дифференцируемость.

8. Формула Ньютона – Лейбница для определенного интеграла.

9. Вычисление определенного интеграла по частям и заменой переменной.

10. Применение определенного интеграла (площадь плоской фигуры, длина дуги кривой, объем тела вращения).

11. Понятие числового ряда и его сумма. Критерий Коши сходимости ряда. Необходимое условие сходимости.

12. Признаки Даламбера и Коши сходимости рядов с неотрицательными членами.

13. Интегральный признак Коши сходимости числового ряда.

14. Знакопеременные числовые ряды. Абсолютная и условная сходимость. Знакочередующиеся ряды. Признак Лейбница.

15. Функциональный ряд. Сумма ряда. Определение равномерной сходимости функционального ряда.

16. Признак Вейерштрассе равномерной сходимости.

17. Свойство равномерно сходящихся функциональных рядов. Терема о непрерывности суммы равномерно сходящегося ряда из непрерывных функций. Теорема о почленном интегрировании и дифференцировании ряда (без доказательства).

18. Степенной ряд. Теорема Абеля.

19. Радиус сходимости степенного ряда. Формула Коши-Адамара для радиуса сходимости степенного ряда.

20. Ряд Тейлора. Теорема Тейлора о разложимости функции в ряд Тейлора. Разложение основных элементарных функций в ряд Тейлора-Маклерона: sin x, cos x, (1+x)a, ln(1+x).

21. Функции многих переменных. Понятие n-мерного евклидова пространства. Множество точек евклидова пространства. Последовательность точек и ее предел. Определение функции нескольких переменных.

22. Предел функции нескольких переменных. Непрерывность функции. Частные производные.

23. Определение дифференцируемой функции нескольких переменных и ее дифференциала. Производные и дифференциалы высших порядков.

24. Формула Тейлора для функции многих переменных. Экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума.

25. Двойной интеграл и его свойства. Сведения двойного интеграла к повторному.

26. Тройной интеграл, сведение его к повторному.

27. Замена переменных в двойном интеграле. Пример случай полярных координат.

28. Замена переменных в тройном интеграле. Цилиндрические и сферические координаты.

29. Вычисление площади гладкой поверхности, заданной параметрически и в явном виде.

30. Определение криволинейных интегралов первого и второго рода, их основные свойства и вычисление.

31. Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования.

32. Поверхностные интегралы первого и второго рода, их основные свойства и вычисления.

33. Теорема Гаусса-Остроградского, ее запись в координатной и векторной (инвариантной) формах.

34. Формула Стокса, ее запись в координатной и векторной (инвариантной) формах.

35. Скалярное и векторное поля. Градиент, дивергенция, ротор. Потенциальное и соленоидальное поля.

36. Оператор Гамильтона (набла), его применение (примеры).

37. Основные понятия, относящиеся к обыкновенным дифференциальным уравнениям (ОДУ) первого порядка: общее и частное решения, общий интеграл, интегральная кривая. Задача Коши, ее геометрический смысл.

38. Интегрирование ОДУ первого порядка с разделяющимися переменными и однородных.

39. Интегрирование линейных ОДУ первого порядка и уравнения Бернулли.

40. Интегрирование ОДУ первого порядка в полных дифференциалах. Интегрирующий множитель.

41. Дифференциальное уравнение первого порядка, не разрешенные относительно производной. Метод введения параметра.

42. Уравнения n-го порядка с постоянными коэффициентами. Характеристические уравнения. Фундаментальная система решений (ФСР) однородного уравнения, общее решение неоднородного уравнения.

43. Система линейных дифференциальных уравнений первого порядка. ФСР однородной системы. Общее решение однородной и неоднородной системы.

1. Определенный интеграл. Интегральная сумма. Верхняя и нижняя интегральные суммы. Их свойства.

Определенный интеграл Римана.

Разбиения отрезков.

Def. ] имеется отрезок (a,b). Система точек x₀, x₁, x₂, x₃,…, x_n называется разбиением отрезка (a,b), если a=x₀<x₁<x₂<x₃<…<x_n=b, то разбиение будем обозначать как p. Отрезки x=[x_k-1,x_k] (k=1,2,3,…,n) называется частичными отрезками разбиения. Символом x_k=x_k-x_k-1 обозначается длинна отрезка разбиения 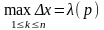- параметр разбиения p. Разбиение отмеченными точками.

Def. ] имеется разбиение p отрезка [a,b] на частичные отрезки x_k, в каждом таком отрезке выберем точку _k, тогда система точек ₁, ₂, ₃,…, _n называется системой отмеченных точек, и обозначается символом , а разбиение с отмеченными точками обозначается (p,).

Def. ] задана функция f(x):[a,b]R Сумма (f;(p,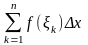))= - называется интегральной суммой функции f, соответствующей разбиению p с соответствующими точками .

Def1. Число I называется интегралом Римана функции f(x) на отрезке [a,b], если >0 ()>0: ((p,)/(p)<)|(f;(p,))-I|< Иначе: lim_0(f;(p,))=I, где число I обозначается как

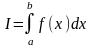
Def2. Функция f(x):[a,b]R называется интегрируемой по Риману, если 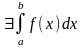. Множество всех интегрируемых по Риману на отрезке [a,b] функций f(x) обозначается как R[a,b].

 Суммы Дарбу.

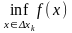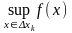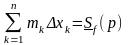Def. ] задана f(x):[a,b]R и пусть p – разбиение отрезка [a,b] на частичные отрезки x_k, k=1,2,3,…,n. Обозначим через m_k точную нижнюю грань т.е. m_k= , а через M_k= . Суммы и 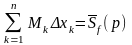называются соответственно нижней и верхней суммами Дарбу. Свойства сумм Дарбу:

1⁰ p 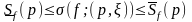m_kf(_k)М_k, m_kx_k f(_k)x_k М_kx_k просумм. получаем 

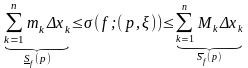
2⁰

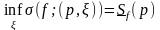
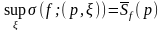
возьмем

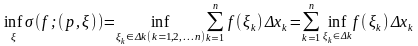
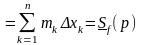(используем независимость ₁,₂,₃,…,_n) 

3⁰ Свойство монотонности сумм Дарбу.

2. Ограниченность интегрируемых функций.

Условия интегрируемости по Риману.

1. Необходимое условие интегрируемости по Риману.

Th1. Если f(x)[a,b]  f(x) – ограничена на [a,b].

Док-во: Предположим противное, что f(x) – неограниченна на [a,b] и пусть p – любое разбиение отрезка [a,b], тогда хотя бы в одном из частичных отрезков x_k функция f(x) неограниченна. Это значит, что f(_k)x_k – это произвольно, выбором точки _kx_k можно сделать как угодно большим по модулю  интегральная сумма (f;(p,)) принимает сколь угодно большие по модулю значения, а это означает, что lim_0(f;(p,))  не существует 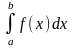для этой функции, что противоречит условию теоремы.

3. Критерий интегрируемости ограниченной на отрезке функции.

Th(критерий Римана).

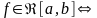f – ограничено на [a,b] и

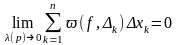
Рассмотрим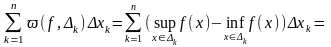

-

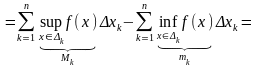
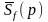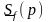
Перейдем к пределу при (p)0 -

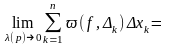
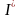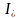
Если 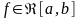, то по теореме Дарбу:

 = = т.е. - = - =0