23. Определение дифференцируемой функции нескольких переменных и ее дифференциала. Производные и дифференциалы высших порядков.

    Пусть функция  u = F(x)  определена в области D и   − фиксированная точка. Дадим приращение каждому аргументу х_ţ :   Величину   будем называть вектором приращения. В свою очередь функция  u  получит приращение равное

Определение 1. Функция   u = F(x)  называется дифференцируемой в т. х , если ее приращение может быть представлено в следующем виде:  

                где

A_ţ = A_ţ(x) и не зависит от Δх, а   − бесконечно малая при

Величина вектора  Δх  равна:  

Используя это обозначение, можно написать 

Легко показать, что

{ }

Определение 2. Главная и линейная часть приращения дифференцируемой функции называется дифференциалом: 

 Вычисляя частные производные ФНП, мы снова получаем функцию тех же переменных, от которой можно взять частную производную, в том числе и по другой переменной (если она, конечно, существует):   Частные производные по одной и той же переменной называются  повторными, а по различным переменным – смешанными. Например: 

Определение 1. Дифференциал от первого дифференциала функции называется вторым дифференциалом:   Аналогично определяются дифференциалы более старших порядков.

   Вычислим второй дифференциал функции двух переменных  . При этом будем считать, что дифференциалы независимых переменных  dx  и  dy – величины постоянные (т.е. не зависят от т.(х,у) и не меняются при вычислении каждого последующего дифференциала).

.

Не трудно видеть, что второй дифференциал представляет собой квадратичную форму от

переменных  dx  и  dy. Матрица этой квадратичной формы есть матрица Гессе, т.е.

d²z = (dx,dy)Г(dx,dy)^T   (см. раздел «Линейная алгебра», квадратичные формы). Кроме того,

второй дифференциал можно записать в символическом виде: 

Можно показать, что в общем случае дифференциал  2 – го порядка функции  u = F(x) равен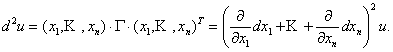 

 Дифференциал  m – го порядка равен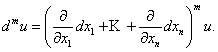    

24. Формула Тейлора для функции многих переменных. Экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума.

Если функция    имеет в некоторой окрестности точки  непрерывные частные производные до (n+1)-го порядка включительно, то для любой точки  из этой окрестности справедлива формула Тейлора n-го порядка:     , где  ,

 ,

 

 Определение. Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М₀(х₀, у₀) верно неравенство

то точка М₀ называется точкой максимума.

  Определение. Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М₀(х₀, у₀) верно неравенство

то точка М₀ называется точкой минимума.

  Теорема. (Необходимые условия экстремума).

Если функция f(x,y) в точке (х₀, у₀) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю  , либо хотя бы одна из них не существует.

  Эту точку (х₀, у₀) будем называть критической точкой.

  Теорема. (Достаточные условия экстремума).

  Пусть в окрестности критической точки (х₀, у₀) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:

1)      Если D(x₀, y₀) > 0, то в точке (х₀, у₀) функция f(x, y) имеет экстремум, если

 - максимум, если   - минимум.

2)      Если D(x₀, y₀) < 0, то в точке (х₀, у₀) функция f(x, y) не имеет экстремума

В случае, если D = 0, вывод о наличии экстремума сделать нельзя.