38. Интегрирование оду первого порядка с разделяющимися переменными и однородных.

.

(13)

Это уравнение сводится к уравнению с разделяющимися переменными относительно новой неизвестной функции u(x) заменой  , или  . Подставляя в (13) y = x·u, y ′ = u + x·u ′, получим   (это - уравнение с разделяющимися переменными),   - это общий интеграл уравнения относительно переменных x, u.  Пример:  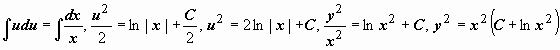   - общее решение уравнения. 

___________________________________________________________________

Если правая часть уравнения

F(x, y, y ',..., y⁽ⁿ⁾ )  =  0,

удовлетворяет условию однородности

F(x, ty, ty ',..., ty⁽ⁿ⁾ ) =  t^k F(x, y, y ',..., y⁽ⁿ⁾ )

то говорят, что это уравнение, однородное относительно неизвестной функции и всех ее производных.

Если в результате каких–либо преобразований порядок n уравнения F(x, y, y ',..., y⁽ⁿ⁾ )  =  0 может быть понижен, то говорят, что уравнение допускает понижение порядка.

К уравнениям, допускающим понижение порядка, относятся уравнения, однородные относительно неизвестной функции и всех ее производных.

 

Порядок такого уравнения можно понизить заменой

Выражение для первой производной от y(x) не содержит производной от z(x):

Поэтому, заменив в исходном уравнении y, y ',..., y⁽ⁿ⁾ их выражениями через z(x), получим относительно z(x) дифференциальное уравнение на единицу меньшего порядка.

39. Интегрирование линейных оду первого порядка и уравнения Бернулли.

Уравнением Бернулли называется уравнение первого порядка вида

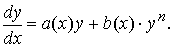
Здесь a(x) и b(x) — известные, непрерывные на [a;b] функции, n > 1.

Заменой z(x) =  y^1-n(x) уравнение Бернулли сводится к линейному уравнению относительно функции z(x):

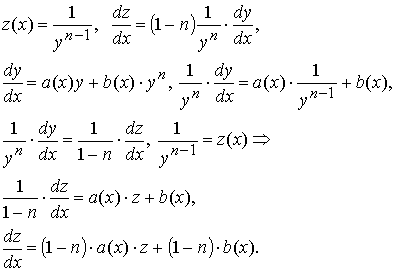
Получили линейное относительно z(x) уравнение:

ДУ первого порядка называется линейным, если неизвестная функция y(x) и её производная   входят в уравнение в первой степени:

.

(14)

Здесь p(x), q(x) - непрерывные функции.  Для решения уравнения (14) представим y(x) в виде произведения двух новых неизвестных функций u(x) и v(x): y(x) = u(x) v(x). Тогда  , и уравнение приводится к виду  , или  . Это уравнение решаем в два этапа: сначала находим функцию v(x) как частное решение уравнения с разделяющимися переменными  ; затем находим u(x) из уравнения  . Итак,   (мы не вводим в это решение произвольную постоянную C, нам достаточно найти одну функцию v(x), обнуляющую слагаемое со скобками в уравнении  ). Теперь уравнение для u(x) запишется как    . Общее решение уравнения (14): 

40. Интегрирование оду первого порядка в полных дифференциалах. Интегрирующий множитель.

Рассмотрим дифференциальное уравнение вида

где P(x,y) и Q(x,y) − функции двух переменных x и y, непрерывные в некоторой области D. Если

то уравнение не будет являться уравнением в полных дифференциалах. Однако мы можем попробовать подобрать так называемый интегрирующий множитель, представляющий собой функцию µ(x,y), такую, что после умножения на нее дифференциальное уравнение преобразуется в уравнение в полных дифференциалах. В таком случае справедливо равенство:

Это условие можно записать в виде:

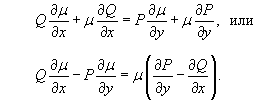
Последнее выражение представляет собой уравнение в частных производных первого порядка, которое определяет интегрирующий множитель µ(x,y). 

41. Дифференциальное уравнение первого порядка, не разрешенные относительно производной. Метод введения параметра.    Рассмотрим уравнение вида

F ( x , y , y ' ) = 0 ,

не разрешённое относительно производной. Если попытаться выразить из него  y ' ,  то можно получить , вообще говоря , несколько уравнений

Геометрически это означает ,  что в каждой точке   задаётся несколько направлений поля (см.рис.2).

Рис. 2

   Следовательно через любую точку  M ( x , y )  может проходить несколько интегральных кривых     . Для того, чтобы выделить из этого множества единственную интегральную кривую, проходящую через заданную точку  M₀ ( x₀ , y₀)  , надо помимо значений  ( x₀ , y₀ )    дополнительно задать в этой точке направление поля    y ' ( x₀) = y '_{0   .}